Robust Maximization of Non-Submodular Objectives
Paper and Code
Mar 14, 2018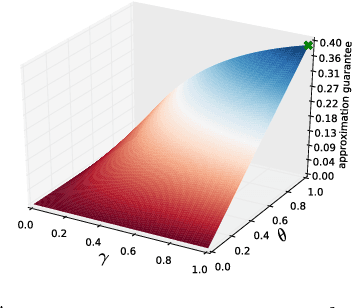
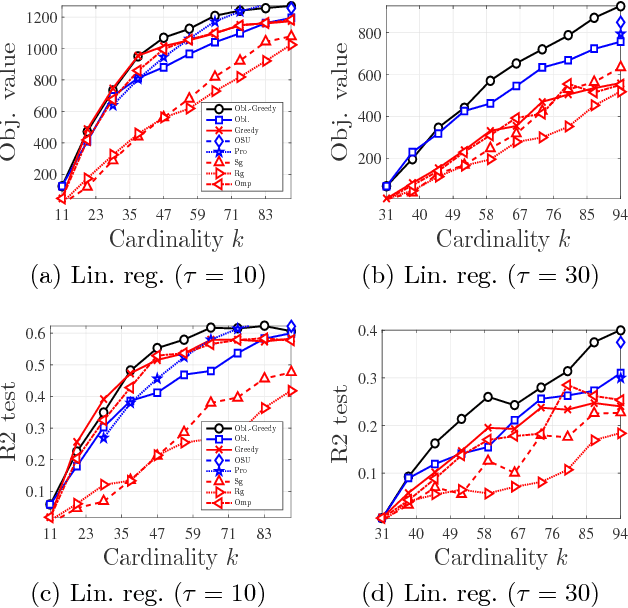
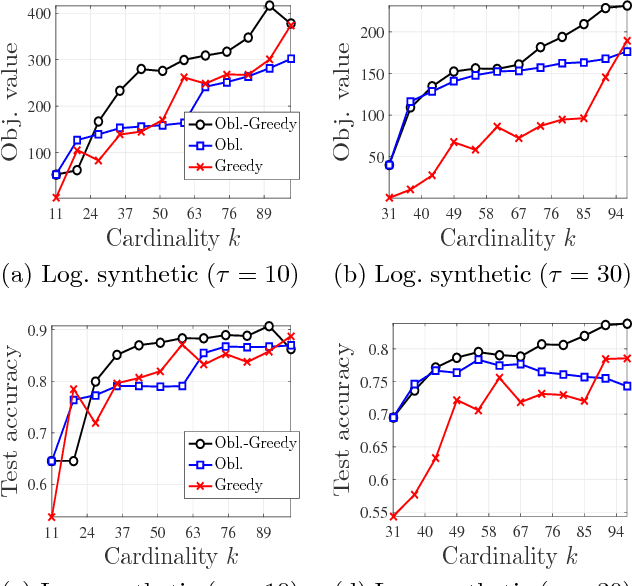
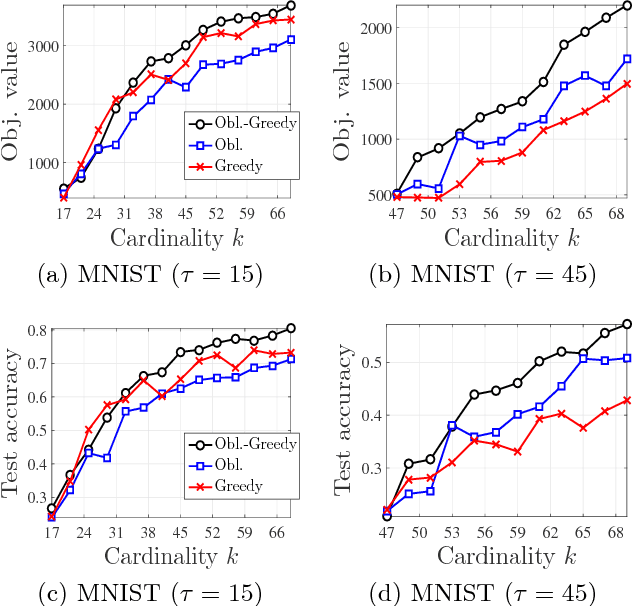
We study the problem of maximizing a monotone set function subject to a cardinality constraint $k$ in the setting where some number of elements $\tau$ is deleted from the returned set. The focus of this work is on the worst-case adversarial setting. While there exist constant-factor guarantees when the function is submodular, there are no guarantees for non-submodular objectives. In this work, we present a new algorithm Oblivious-Greedy and prove the first constant-factor approximation guarantees for a wider class of non-submodular objectives. The obtained theoretical bounds are the first constant-factor bounds that also hold in the linear regime, i.e. when the number of deletions $\tau$ is linear in $k$. Our bounds depend on established parameters such as the submodularity ratio and some novel ones such as the inverse curvature. We bound these parameters for two important objectives including support selection and variance reduction. Finally, we numerically demonstrate the robust performance of Oblivious-Greedy for these two objectives on various datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge