Rethinking Graph Neural Networks for the Graph Coloring Problem

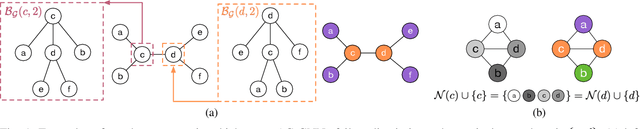
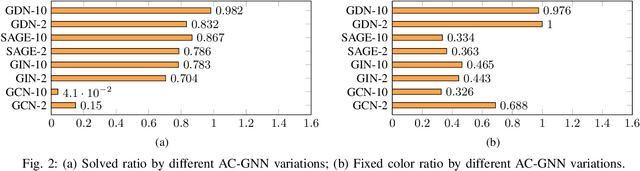
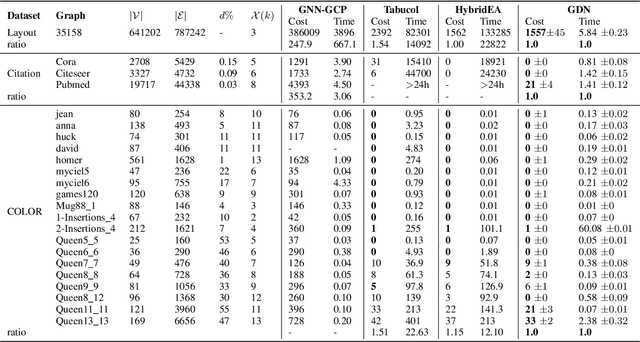
Graph coloring, a classical and critical NP-hard problem, is the problem of assigning connected nodes as different colors as possible. However, we observe that state-of-the-art GNNs are less successful in the graph coloring problem. We analyze the reasons from two perspectives. First, most GNNs fail to generalize the task under homophily to heterophily, i.e., graphs where connected nodes are assigned different colors. Second, GNNs are bounded by the network depth, making them possible to be a local method, which has been demonstrated to be non-optimal in Maximum Independent Set (MIS) problem. In this paper, we focus on the aggregation-combine GNNs (AC-GNNs), a popular class of GNNs. We first define the power of AC-GNNs in the coloring problem as the capability to assign nodes different colors. The definition is different with previous one that is based on the assumption of homophily. We identify node pairs that AC-GNNs fail to discriminate. Furthermore, we show that any AC-GNN is a local coloring method, and any local coloring method is non-optimal by exploring the limits of local methods over sparse random graphs, thereby demonstrating the non-optimality of AC-GNNs due to its local property. We then prove the positive correlation between model depth and its coloring power. Moreover, we discuss the color equivariance of graphs to tackle some practical constraints such as the pre-fixing constraints. Following the discussions above, we summarize a series of rules a series of rules that make a GNN color equivariant and powerful in the coloring problem. Then, we propose a simple AC-GNN variation satisfying these rules. We empirically validate our theoretical findings and demonstrate that our simple model substantially outperforms state-of-the-art heuristic algorithms in both quality and runtime.

The Gambler's Problem and Beyond

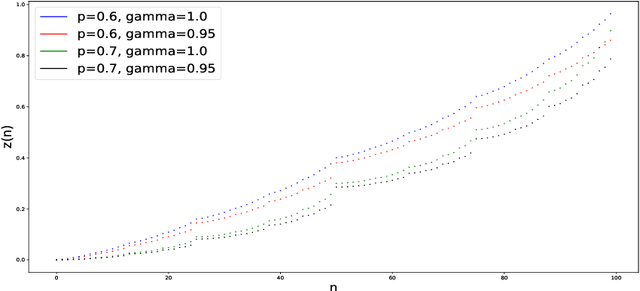
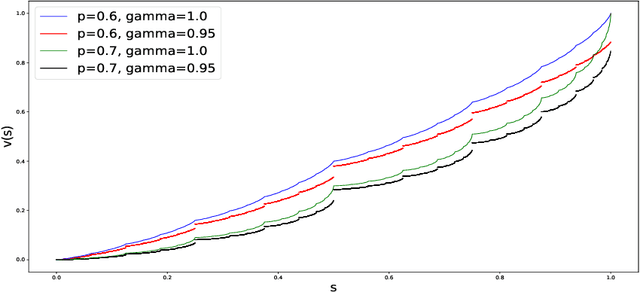
We analyze the Gambler's problem, a simple reinforcement learning problem where the gambler has the chance to double or lose their bets until the target is reached. This is an early example introduced in the reinforcement learning textbook by Sutton and Barto (2018), where they mention an interesting pattern of the optimal value function with high-frequency components and repeating non-smooth points. It is however without further investigation. We provide the exact formula for the optimal value function for both the discrete and the continuous cases. Though simple as it might seem, the value function is pathological: fractal, self-similar, derivative taking either zero or infinity, not smooth on any interval, and not written as elementary functions. It is in fact one of the generalized Cantor functions, where it holds a complexity that has been uncharted thus far. Our analyses could lead insights into improving value function approximation, gradient-based algorithms, and Q-learning, in real applications and implementations.

On the Worst-Case Approximability of Sparse PCA

It is well known that Sparse PCA (Sparse Principal Component Analysis) is NP-hard to solve exactly on worst-case instances. What is the complexity of solving Sparse PCA approximately? Our contributions include: 1) a simple and efficient algorithm that achieves an $n^{-1/3}$-approximation; 2) NP-hardness of approximation to within $(1-\varepsilon)$, for some small constant $\varepsilon > 0$; 3) SSE-hardness of approximation to within any constant factor; and 4) an $\exp\exp\left(\Omega\left(\sqrt{\log \log n}\right)\right)$ ("quasi-quasi-polynomial") gap for the standard semidefinite program.