Information Bargaining: Bilateral Commitment in Bayesian Persuasion

Bayesian persuasion, an extension of cheap-talk communication, involves an informed sender committing to a signaling scheme to influence a receiver's actions. Compared to cheap talk, this sender's commitment enables the receiver to verify the incentive compatibility of signals beforehand, facilitating cooperation. While effective in one-shot scenarios, Bayesian persuasion faces computational complexity (NP-hardness) when extended to long-term interactions, where the receiver may adopt dynamic strategies conditional on past outcomes and future expectations. To address this complexity, we introduce the bargaining perspective, which allows: (1) a unified framework and well-structured solution concept for long-term persuasion, with desirable properties such as fairness and Pareto efficiency; (2) a clear distinction between two previously conflated advantages: the sender's informational advantage and first-proposer advantage. With only modest modifications to the standard setting, this perspective makes explicit the common knowledge of the game structure and grants the receiver comparable commitment capabilities, thereby reinterpreting classic one-sided persuasion as a balanced information bargaining framework. The framework is validated through a two-stage validation-and-inference paradigm: We first demonstrate that GPT-o3 and DeepSeek-R1, out of publicly available LLMs, reliably handle standard tasks; We then apply them to persuasion scenarios to test that the outcomes align with what our information-bargaining framework suggests. All code, results, and terminal logs are publicly available at github.com/YueLin301/InformationBargaining.

Bayesian Persuasion as a Bargaining Game

Bayesian persuasion, an extension of cheap-talk communication, involves an informed sender committing to a signaling scheme to influence a receiver's actions. Compared to cheap talk, this sender's commitment enables the receiver to verify the incentive compatibility of signals beforehand, facilitating cooperation. While effective in one-shot scenarios, Bayesian persuasion faces computational complexity (NP-hardness) when extended to long-term interactions, where the receiver may adopt dynamic strategies conditional on past outcomes and future expectations. To address this complexity, we introduce the bargaining perspective, which allows: (1) a unified framework and well-structured solution concept for long-term persuasion, with desirable properties such as fairness and Pareto efficiency; (2) a clear distinction between two previously conflated advantages: the sender's informational advantage and first-proposer advantage. With only modest modifications to the standard setting, this perspective makes explicit the common knowledge of the game structure and grants the receiver comparable commitment capabilities, thereby reinterpreting classic one-sided persuasion as a balanced information bargaining framework. The framework is validated through a two-stage validation-and-inference paradigm: We first demonstrate that GPT-o3 and DeepSeek-R1, out of publicly available LLMs, reliably handle standard tasks; We then apply them to persuasion scenarios to test that the outcomes align with what our information-bargaining framework suggests. All code, results, and terminal logs are publicly available at github.com/YueLin301/InformationBargaining.

ADG: Ambient Diffusion-Guided Dataset Recovery for Corruption-Robust Offline Reinforcement Learning

Real-world datasets collected from sensors or human inputs are prone to noise and errors, posing significant challenges for applying offline reinforcement learning (RL). While existing methods have made progress in addressing corrupted actions and rewards, they remain insufficient for handling corruption in high-dimensional state spaces and for cases where multiple elements in the dataset are corrupted simultaneously. Diffusion models, known for their strong denoising capabilities, offer a promising direction for this problem-but their tendency to overfit noisy samples limits their direct applicability. To overcome this, we propose Ambient Diffusion-Guided Dataset Recovery (ADG), a novel approach that pioneers the use of diffusion models to tackle data corruption in offline RL. First, we introduce Ambient Denoising Diffusion Probabilistic Models (DDPM) from approximated distributions, which enable learning on partially corrupted datasets with theoretical guarantees. Second, we use the noise-prediction property of Ambient DDPM to distinguish between clean and corrupted data, and then use the clean subset to train a standard DDPM. Third, we employ the trained standard DDPM to refine the previously identified corrupted data, enhancing data quality for subsequent offline RL training. A notable strength of ADG is its versatility-it can be seamlessly integrated with any offline RL algorithm. Experiments on a range of benchmarks, including MuJoCo, Kitchen, and Adroit, demonstrate that ADG effectively mitigates the impact of corrupted data and improves the robustness of offline RL under various noise settings, achieving state-of-the-art results.

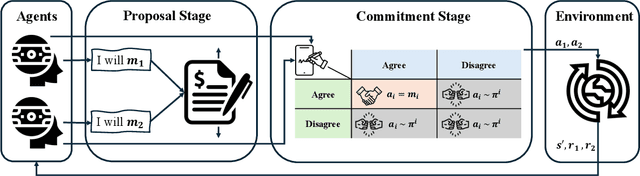
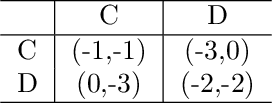
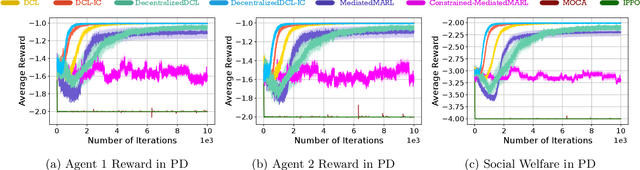
Learning to Negotiate via Voluntary Commitment

The partial alignment and conflict of autonomous agents lead to mixed-motive scenarios in many real-world applications. However, agents may fail to cooperate in practice even when cooperation yields a better outcome. One well known reason for this failure comes from non-credible commitments. To facilitate commitments among agents for better cooperation, we define Markov Commitment Games (MCGs), a variant of commitment games, where agents can voluntarily commit to their proposed future plans. Based on MCGs, we propose a learnable commitment protocol via policy gradients. We further propose incentive-compatible learning to accelerate convergence to equilibria with better social welfare. Experimental results in challenging mixed-motive tasks demonstrate faster empirical convergence and higher returns for our method compared with its counterparts. Our code is available at https://github.com/shuhui-zhu/DCL.

Verbalized Bayesian Persuasion

Information design (ID) explores how a sender influence the optimal behavior of receivers to achieve specific objectives. While ID originates from everyday human communication, existing game-theoretic and machine learning methods often model information structures as numbers, which limits many applications to toy games. This work leverages LLMs and proposes a verbalized framework in Bayesian persuasion (BP), which extends classic BP to real-world games involving human dialogues for the first time. Specifically, we map the BP to a verbalized mediator-augmented extensive-form game, where LLMs instantiate the sender and receiver. To efficiently solve the verbalized game, we propose a generalized equilibrium-finding algorithm combining LLM and game solver. The algorithm is reinforced with techniques including verbalized commitment assumptions, verbalized obedience constraints, and information obfuscation. Numerical experiments in dialogue scenarios, such as recommendation letters, courtroom interactions, and law enforcement, validate that our framework can both reproduce theoretical results in classic BP and discover effective persuasion strategies in more complex natural language and multi-stage scenarios.

On the Decomposition of Differential Game

To understand the complexity of the dynamic of learning in differential games, we decompose the game into components where the dynamic is well understood. One of the possible tools is Helmholtz's theorem, which can decompose a vector field into a potential and a harmonic component. This has been shown to be effective in finite and normal-form games. However, applying Helmholtz's theorem by connecting it with the Hodge theorem on $\mathbb{R}^n$ (which is the strategy space of differential game) is non-trivial due to the non-compactness of $\mathbb{R}^n$. Bridging the dynamic-strategic disconnect through Hodge/Helmoltz's theorem in differential games is then left as an open problem \cite{letcher2019differentiable}. In this work, we provide two decompositions of differential games to answer this question: the first as an exact scalar potential part, a near vector potential part, and a non-strategic part; the second as a near scalar potential part, an exact vector potential part, and a non-strategic part. We show that scalar potential games coincide with potential games proposed by \cite{monderer1996potential}, where the gradient descent dynamic can successfully find the Nash equilibrium. For the vector potential game, we show that the individual gradient field is divergence-free, in which case the gradient descent dynamic may either be divergent or recurrent.

Learning to Construct Implicit Communication Channel

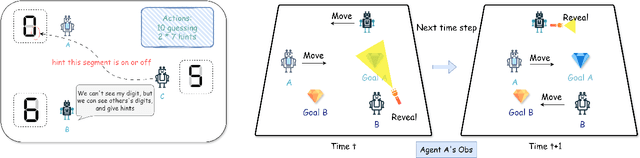
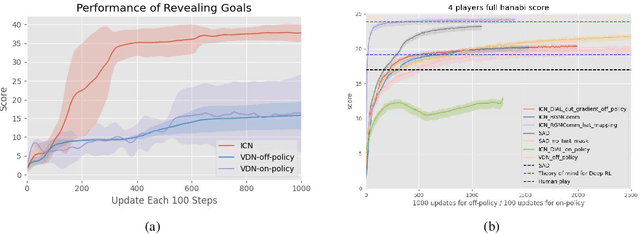
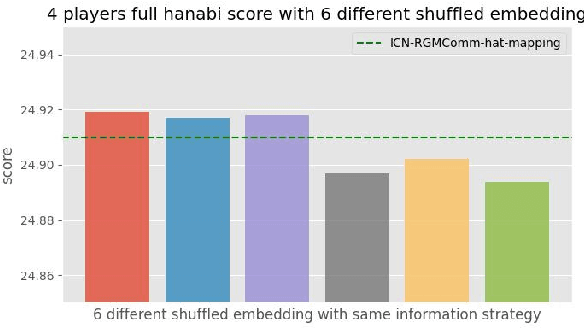
Effective communication is an essential component in collaborative multi-agent systems. Situations where explicit messaging is not feasible have been common in human society throughout history, which motivate the study of implicit communication. Previous works on learning implicit communication mostly rely on theory of mind (ToM), where agents infer the mental states and intentions of others by interpreting their actions. However, ToM-based methods become less effective in making accurate inferences in complex tasks. In this work, we propose the Implicit Channel Protocol (ICP) framework, which allows agents to construct implicit communication channels similar to the explicit ones. ICP leverages a subset of actions, denoted as the scouting actions, and a mapping between information and these scouting actions that encodes and decodes the messages. We propose training algorithms for agents to message and act, including learning with a randomly initialized information map and with a delayed information map. The efficacy of ICP has been tested on the tasks of Guessing Number, Revealing Goals, and Hanabi, where ICP significantly outperforms baseline methods through more efficient information transmission.

A Comprehensive Framework for Analyzing the Convergence of Adam: Bridging the Gap with SGD

Adaptive Moment Estimation (Adam) is a cornerstone optimization algorithm in deep learning, widely recognized for its flexibility with adaptive learning rates and efficiency in handling large-scale data. However, despite its practical success, the theoretical understanding of Adam's convergence has been constrained by stringent assumptions, such as almost surely bounded stochastic gradients or uniformly bounded gradients, which are more restrictive than those typically required for analyzing stochastic gradient descent (SGD). In this paper, we introduce a novel and comprehensive framework for analyzing the convergence properties of Adam. This framework offers a versatile approach to establishing Adam's convergence. Specifically, we prove that Adam achieves asymptotic (last iterate sense) convergence in both the almost sure sense and the \(L_1\) sense under the relaxed assumptions typically used for SGD, namely \(L\)-smoothness and the ABC inequality. Meanwhile, under the same assumptions, we show that Adam attains non-asymptotic sample complexity bounds similar to those of SGD.

Asymptotic and Non-Asymptotic Convergence Analysis of AdaGrad for Non-Convex Optimization via Novel Stopping Time-based Analysis

Adaptive optimizers have emerged as powerful tools in deep learning, dynamically adjusting the learning rate based on iterative gradients. These adaptive methods have significantly succeeded in various deep learning tasks, outperforming stochastic gradient descent (SGD). However, although AdaGrad is a cornerstone adaptive optimizer, its theoretical analysis is inadequate in addressing asymptotic convergence and non-asymptotic convergence rates on non-convex optimization. This study aims to provide a comprehensive analysis and complete picture of AdaGrad. We first introduce a novel stopping time technique from probabilistic theory to establish stability for the norm version of AdaGrad under milder conditions. We further derive two forms of asymptotic convergence: almost sure and mean-square. Furthermore, we demonstrate the near-optimal non-asymptotic convergence rate measured by the average-squared gradients in expectation, which is rarely explored and stronger than the existing high-probability results, under the mild assumptions. The techniques developed in this work are potentially independent of interest for future research on other adaptive stochastic algorithms.

Robust Decision Transformer: Tackling Data Corruption in Offline RL via Sequence Modeling

Learning policies from offline datasets through offline reinforcement learning (RL) holds promise for scaling data-driven decision-making and avoiding unsafe and costly online interactions. However, real-world data collected from sensors or humans often contains noise and errors, posing a significant challenge for existing offline RL methods. Our study indicates that traditional offline RL methods based on temporal difference learning tend to underperform Decision Transformer (DT) under data corruption, especially when the amount of data is limited. This suggests the potential of sequential modeling for tackling data corruption in offline RL. To further unleash the potential of sequence modeling methods, we propose Robust Decision Transformer (RDT) by incorporating several robust techniques. Specifically, we introduce Gaussian weighted learning and iterative data correction to reduce the effect of corrupted data. Additionally, we leverage embedding dropout to enhance the model's resistance to erroneous inputs. Extensive experiments on MoJoCo, KitChen, and Adroit tasks demonstrate RDT's superior performance under diverse data corruption compared to previous methods. Moreover, RDT exhibits remarkable robustness in a challenging setting that combines training-time data corruption with testing-time observation perturbations. These results highlight the potential of robust sequence modeling for learning from noisy or corrupted offline datasets, thereby promoting the reliable application of offline RL in real-world tasks.