Ruxuan Li
Rethinking Graph Neural Networks for the Graph Coloring Problem
Aug 19, 2022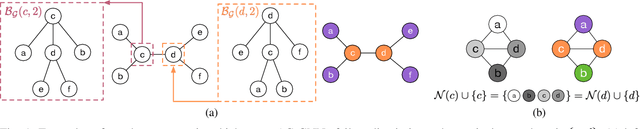
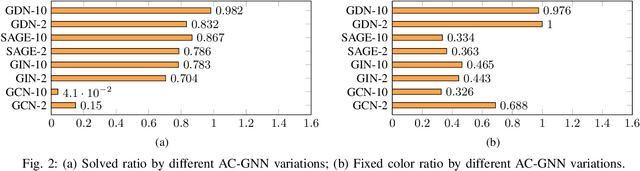

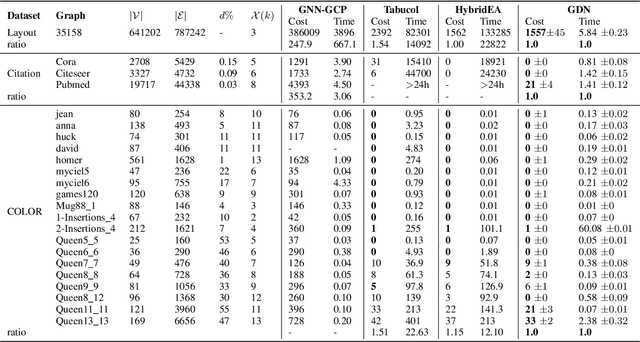
Abstract:Graph coloring, a classical and critical NP-hard problem, is the problem of assigning connected nodes as different colors as possible. However, we observe that state-of-the-art GNNs are less successful in the graph coloring problem. We analyze the reasons from two perspectives. First, most GNNs fail to generalize the task under homophily to heterophily, i.e., graphs where connected nodes are assigned different colors. Second, GNNs are bounded by the network depth, making them possible to be a local method, which has been demonstrated to be non-optimal in Maximum Independent Set (MIS) problem. In this paper, we focus on the aggregation-combine GNNs (AC-GNNs), a popular class of GNNs. We first define the power of AC-GNNs in the coloring problem as the capability to assign nodes different colors. The definition is different with previous one that is based on the assumption of homophily. We identify node pairs that AC-GNNs fail to discriminate. Furthermore, we show that any AC-GNN is a local coloring method, and any local coloring method is non-optimal by exploring the limits of local methods over sparse random graphs, thereby demonstrating the non-optimality of AC-GNNs due to its local property. We then prove the positive correlation between model depth and its coloring power. Moreover, we discuss the color equivariance of graphs to tackle some practical constraints such as the pre-fixing constraints. Following the discussions above, we summarize a series of rules a series of rules that make a GNN color equivariant and powerful in the coloring problem. Then, we propose a simple AC-GNN variation satisfying these rules. We empirically validate our theoretical findings and demonstrate that our simple model substantially outperforms state-of-the-art heuristic algorithms in both quality and runtime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge