M3: Mamba-assisted Multi-Circuit Optimization via MBRL with Effective Scheduling

Recent advancements in reinforcement learning (RL) for analog circuit optimization have demonstrated significant potential for improving sample efficiency and generalization across diverse circuit topologies and target specifications. However, there are challenges such as high computational overhead, the need for bespoke models for each circuit. To address them, we propose M3, a novel Model-based RL (MBRL) method employing the Mamba architecture and effective scheduling. The Mamba architecture, known as a strong alternative to the transformer architecture, enables multi-circuit optimization with distinct parameters and target specifications. The effective scheduling strategy enhances sample efficiency by adjusting crucial MBRL training parameters. To the best of our knowledge, M3 is the first method for multi-circuit optimization by leveraging both the Mamba architecture and a MBRL with effective scheduling. As a result, it significantly improves sample efficiency compared to existing RL methods.

Rethinking Graph Neural Networks for the Graph Coloring Problem

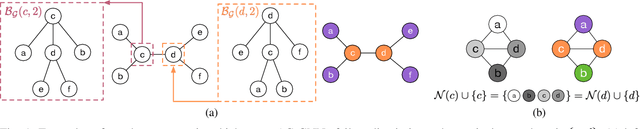
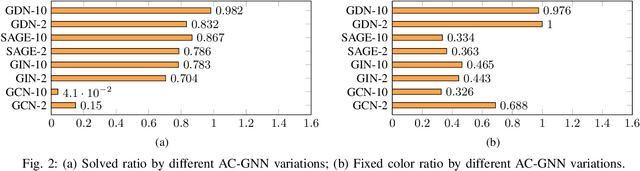
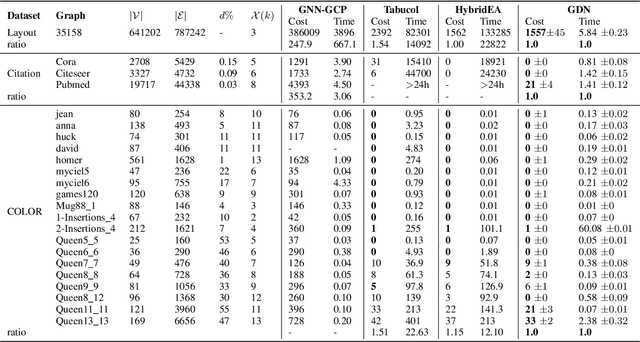
Graph coloring, a classical and critical NP-hard problem, is the problem of assigning connected nodes as different colors as possible. However, we observe that state-of-the-art GNNs are less successful in the graph coloring problem. We analyze the reasons from two perspectives. First, most GNNs fail to generalize the task under homophily to heterophily, i.e., graphs where connected nodes are assigned different colors. Second, GNNs are bounded by the network depth, making them possible to be a local method, which has been demonstrated to be non-optimal in Maximum Independent Set (MIS) problem. In this paper, we focus on the aggregation-combine GNNs (AC-GNNs), a popular class of GNNs. We first define the power of AC-GNNs in the coloring problem as the capability to assign nodes different colors. The definition is different with previous one that is based on the assumption of homophily. We identify node pairs that AC-GNNs fail to discriminate. Furthermore, we show that any AC-GNN is a local coloring method, and any local coloring method is non-optimal by exploring the limits of local methods over sparse random graphs, thereby demonstrating the non-optimality of AC-GNNs due to its local property. We then prove the positive correlation between model depth and its coloring power. Moreover, we discuss the color equivariance of graphs to tackle some practical constraints such as the pre-fixing constraints. Following the discussions above, we summarize a series of rules a series of rules that make a GNN color equivariant and powerful in the coloring problem. Then, we propose a simple AC-GNN variation satisfying these rules. We empirically validate our theoretical findings and demonstrate that our simple model substantially outperforms state-of-the-art heuristic algorithms in both quality and runtime.

RobustAnalog: Fast Variation-Aware Analog Circuit Design Via Multi-task RL

Analog/mixed-signal circuit design is one of the most complex and time-consuming stages in the whole chip design process. Due to various process, voltage, and temperature (PVT) variations from chip manufacturing, analog circuits inevitably suffer from performance degradation. Although there has been plenty of work on automating analog circuit design under the typical condition, limited research has been done on exploring robust designs under real and unpredictable silicon variations. Automatic analog design against variations requires prohibitive computation and time costs. To address the challenge, we present RobustAnalog, a robust circuit design framework that involves the variation information in the optimization process. Specifically, circuit optimizations under different variations are considered as a set of tasks. Similarities among tasks are leveraged and competitions are alleviated to realize a sample-efficient multi-task training. Moreover, RobustAnalog prunes the task space according to the current performance in each iteration, leading to a further simulation cost reduction. In this way, RobustAnalog can rapidly produce a set of circuit parameters that satisfies diverse constraints (e.g. gain, bandwidth, noise...) across variations. We compare RobustAnalog with Bayesian optimization, Evolutionary algorithm, and Deep Deterministic Policy Gradient (DDPG) and demonstrate that RobustAnalog can significantly reduce required optimization time by 14-30 times. Therefore, our study provides a feasible method to handle various real silicon conditions.