Stability Evaluation via Distributional Perturbation Analysis

The performance of learning models often deteriorates when deployed in out-of-sample environments. To ensure reliable deployment, we propose a stability evaluation criterion based on distributional perturbations. Conceptually, our stability evaluation criterion is defined as the minimal perturbation required on our observed dataset to induce a prescribed deterioration in risk evaluation. In this paper, we utilize the optimal transport (OT) discrepancy with moment constraints on the \textit{(sample, density)} space to quantify this perturbation. Therefore, our stability evaluation criterion can address both \emph{data corruptions} and \emph{sub-population shifts} -- the two most common types of distribution shifts in real-world scenarios. To further realize practical benefits, we present a series of tractable convex formulations and computational methods tailored to different classes of loss functions. The key technical tool to achieve this is the strong duality theorem provided in this paper. Empirically, we validate the practical utility of our stability evaluation criterion across a host of real-world applications. These empirical studies showcase the criterion's ability not only to compare the stability of different learning models and features but also to provide valuable guidelines and strategies to further improve models.

Spurious Stationarity and Hardness Results for Mirror Descent

Despite the considerable success of Bregman proximal-type algorithms, such as mirror descent, in machine learning, a critical question remains: Can existing stationarity measures, often based on Bregman divergence, reliably distinguish between stationary and non-stationary points? In this paper, we present a groundbreaking finding: All existing stationarity measures necessarily imply the existence of spurious stationary points. We further establish an algorithmic independent hardness result: Bregman proximal-type algorithms are unable to escape from a spurious stationary point in finite steps when the initial point is unfavorable, even for convex problems. Our hardness result points out the inherent distinction between Euclidean and Bregman geometries, and introduces both fundamental theoretical and numerical challenges to both machine learning and optimization communities.

Automatic Outlier Rectification via Optimal Transport

In this paper, we propose a novel conceptual framework to detect outliers using optimal transport with a concave cost function. Conventional outlier detection approaches typically use a two-stage procedure: first, outliers are detected and removed, and then estimation is performed on the cleaned data. However, this approach does not inform outlier removal with the estimation task, leaving room for improvement. To address this limitation, we propose an automatic outlier rectification mechanism that integrates rectification and estimation within a joint optimization framework. We take the first step to utilize an optimal transport distance with a concave cost function to construct a rectification set in the space of probability distributions. Then, we select the best distribution within the rectification set to perform the estimation task. Notably, the concave cost function we introduced in this paper is the key to making our estimator effectively identify the outlier during the optimization process. We discuss the fundamental differences between our estimator and optimal transport-based distributionally robust optimization estimator. finally, we demonstrate the effectiveness and superiority of our approach over conventional approaches in extensive simulation and empirical analyses for mean estimation, least absolute regression, and the fitting of option implied volatility surfaces.

Unifying Distributionally Robust Optimization via Optimal Transport Theory

In the past few years, there has been considerable interest in two prominent approaches for Distributionally Robust Optimization (DRO): Divergence-based and Wasserstein-based methods. The divergence approach models misspecification in terms of likelihood ratios, while the latter models it through a measure of distance or cost in actual outcomes. Building upon these advances, this paper introduces a novel approach that unifies these methods into a single framework based on optimal transport (OT) with conditional moment constraints. Our proposed approach, for example, makes it possible for optimal adversarial distributions to simultaneously perturb likelihood and outcomes, while producing an optimal (in an optimal transport sense) coupling between the baseline model and the adversarial model.Additionally, the paper investigates several duality results and presents tractable reformulations that enhance the practical applicability of this unified framework.

A Convergent Single-Loop Algorithm for Relaxation of Gromov-Wasserstein in Graph Data

In this work, we present the Bregman Alternating Projected Gradient (BAPG) method, a single-loop algorithm that offers an approximate solution to the Gromov-Wasserstein (GW) distance. We introduce a novel relaxation technique that balances accuracy and computational efficiency, albeit with some compromises in the feasibility of the coupling map. Our analysis is based on the observation that the GW problem satisfies the Luo-Tseng error bound condition, which relates to estimating the distance of a point to the critical point set of the GW problem based on the optimality residual. This observation allows us to provide an approximation bound for the distance between the fixed-point set of BAPG and the critical point set of GW. Moreover, under a mild technical assumption, we can show that BAPG converges to its fixed point set. The effectiveness of BAPG has been validated through comprehensive numerical experiments in graph alignment and partition tasks, where it outperforms existing methods in terms of both solution quality and wall-clock time.

Outlier-Robust Gromov Wasserstein for Graph Data

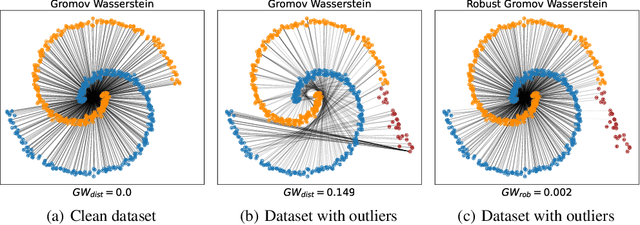
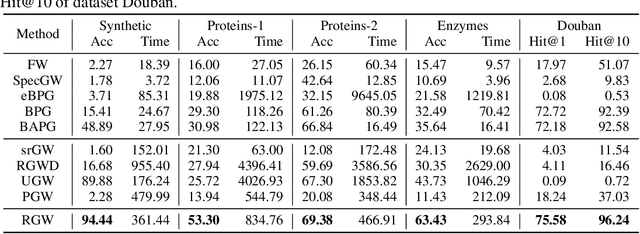
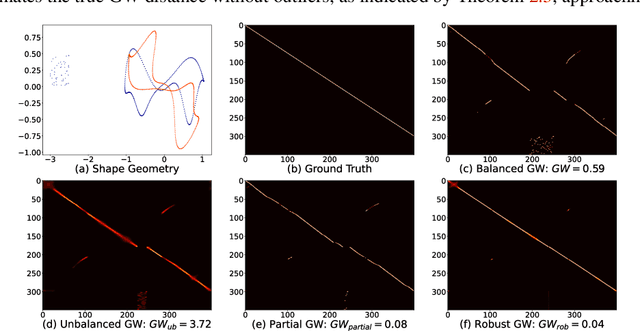
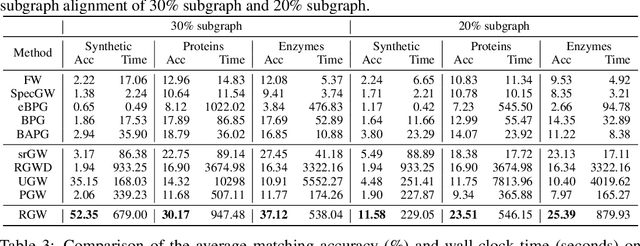
Gromov Wasserstein (GW) distance is a powerful tool for comparing and aligning probability distributions supported on different metric spaces. It has become the main modeling technique for aligning heterogeneous data for a wide range of graph learning tasks. However, the GW distance is known to be highly sensitive to outliers, which can result in large inaccuracies if the outliers are given the same weight as other samples in the objective function. To mitigate this issue, we introduce a new and robust version of the GW distance called RGW. RGW features optimistically perturbed marginal constraints within a $\varphi$-divergence based ambiguity set. To make the benefits of RGW more accessible in practice, we develop a computationally efficient algorithm, Bregman proximal alternating linearization minimization, with a theoretical convergence guarantee. Through extensive experimentation, we validate our theoretical results and demonstrate the effectiveness of RGW on real-world graph learning tasks, such as subgraph matching and partial shape correspondence.

Robust Attributed Graph Alignment via Joint Structure Learning and Optimal Transport

Graph alignment, which aims at identifying corresponding entities across multiple networks, has been widely applied in various domains. As the graphs to be aligned are usually constructed from different sources, the inconsistency issues of structures and features between two graphs are ubiquitous in real-world applications. Most existing methods follow the ``embed-then-cross-compare'' paradigm, which computes node embeddings in each graph and then processes node correspondences based on cross-graph embedding comparison. However, we find these methods are unstable and sub-optimal when structure or feature inconsistency appears. To this end, we propose SLOTAlign, an unsupervised graph alignment framework that jointly performs Structure Learning and Optimal Transport Alignment. We convert graph alignment to an optimal transport problem between two intra-graph matrices without the requirement of cross-graph comparison. We further incorporate multi-view structure learning to enhance graph representation power and reduce the effect of structure and feature inconsistency inherited across graphs. Moreover, an alternating scheme based algorithm has been developed to address the joint optimization problem in SLOTAlign, and the provable convergence result is also established. Finally, we conduct extensive experiments on six unsupervised graph alignment datasets and the DBP15K knowledge graph (KG) alignment benchmark dataset. The proposed SLOTAlign shows superior performance and strongest robustness over seven unsupervised graph alignment methods and five specialized KG alignment methods.

Doubly Smoothed GDA: Global Convergent Algorithm for Constrained Nonconvex-Nonconcave Minimax Optimization

Nonconvex-nonconcave minimax optimization has been the focus of intense research over the last decade due to its broad applications in machine learning and operation research. Unfortunately, most existing algorithms cannot be guaranteed to converge and always suffer from limit cycles. Their global convergence relies on certain conditions that are difficult to check, including but not limited to the global Polyak-\L{}ojasiewicz condition, the existence of a solution satisfying the weak Minty variational inequality and $\alpha$-interaction dominant condition. In this paper, we develop the first provably convergent algorithm called doubly smoothed gradient descent ascent method, which gets rid of the limit cycle without requiring any additional conditions. We further show that the algorithm has an iteration complexity of $\mathcal{O}(\epsilon^{-4})$ for finding a game stationary point, which matches the best iteration complexity of single-loop algorithms under nonconcave-concave settings. The algorithm presented here opens up a new path for designing provable algorithms for nonconvex-nonconcave minimax optimization problems.

Synthetic Principal Component Design: Fast Covariate Balancing with Synthetic Controls

The optimal design of experiments typically involves solving an NP-hard combinatorial optimization problem. In this paper, we aim to develop a globally convergent and practically efficient optimization algorithm. Specifically, we consider a setting where the pre-treatment outcome data is available and the synthetic control estimator is invoked. The average treatment effect is estimated via the difference between the weighted average outcomes of the treated and control units, where the weights are learned from the observed data. {Under this setting, we surprisingly observed that the optimal experimental design problem could be reduced to a so-called \textit{phase synchronization} problem.} We solve this problem via a normalized variant of the generalized power method with spectral initialization. On the theoretical side, we establish the first global optimality guarantee for experiment design when pre-treatment data is sampled from certain data-generating processes. Empirically, we conduct extensive experiments to demonstrate the effectiveness of our method on both the US Bureau of Labor Statistics and the Abadie-Diemond-Hainmueller California Smoking Data. In terms of the root mean square error, our algorithm surpasses the random design by a large margin.

Tikhonov Regularization is Optimal Transport Robust under Martingale Constraints

Distributionally robust optimization has been shown to offer a principled way to regularize learning models. In this paper, we find that Tikhonov regularization is distributionally robust in an optimal transport sense (i.e., if an adversary chooses distributions in a suitable optimal transport neighborhood of the empirical measure), provided that suitable martingale constraints are also imposed. Further, we introduce a relaxation of the martingale constraints which not only provides a unified viewpoint to a class of existing robust methods but also leads to new regularization tools. To realize these novel tools, tractable computational algorithms are proposed. As a byproduct, the strong duality theorem proved in this paper can be potentially applied to other problems of independent interest.