Explicit Preference Optimization: No Need for an Implicit Reward Model

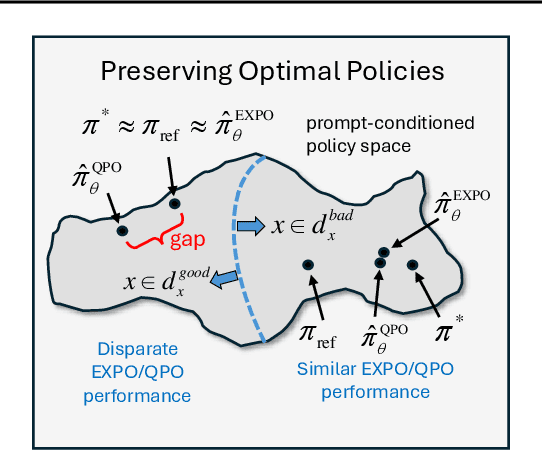
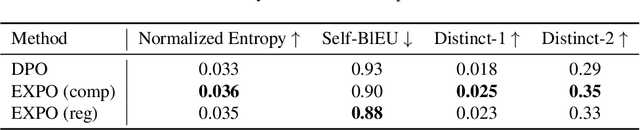
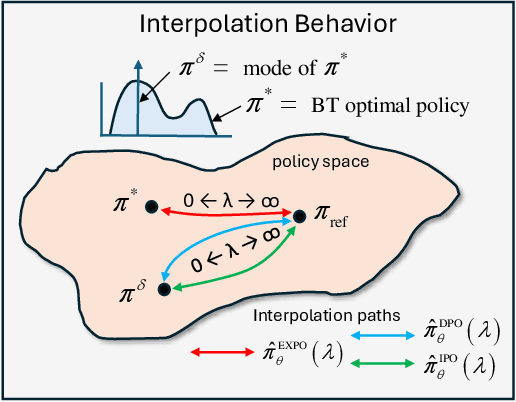
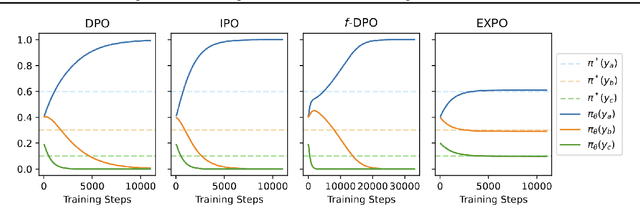
The generated responses of large language models (LLMs) are often fine-tuned to human preferences through a process called reinforcement learning from human feedback (RLHF). As RLHF relies on a challenging training sequence, whereby a separate reward model is independently learned and then later applied to LLM policy updates, ongoing research effort has targeted more straightforward alternatives. In this regard, direct preference optimization (DPO) and its many offshoots circumvent the need for a separate reward training step. Instead, through the judicious use of a reparameterization trick that induces an \textit{implicit} reward, DPO and related methods consolidate learning to the minimization of a single loss function. And yet despite demonstrable success in some real-world settings, we prove that DPO-based objectives are nonetheless subject to sub-optimal regularization and counter-intuitive interpolation behaviors, underappreciated artifacts of the reparameterizations upon which they are based. To this end, we introduce an \textit{explicit} preference optimization framework termed EXPO that requires no analogous reparameterization to achieve an implicit reward. Quite differently, we merely posit intuitively-appealing regularization factors from scratch that transparently avoid the potential pitfalls of key DPO variants, provably satisfying regularization desiderata that prior methods do not. Empirical results serve to corroborate our analyses and showcase the efficacy of EXPO.

A Convergent Single-Loop Algorithm for Relaxation of Gromov-Wasserstein in Graph Data

In this work, we present the Bregman Alternating Projected Gradient (BAPG) method, a single-loop algorithm that offers an approximate solution to the Gromov-Wasserstein (GW) distance. We introduce a novel relaxation technique that balances accuracy and computational efficiency, albeit with some compromises in the feasibility of the coupling map. Our analysis is based on the observation that the GW problem satisfies the Luo-Tseng error bound condition, which relates to estimating the distance of a point to the critical point set of the GW problem based on the optimality residual. This observation allows us to provide an approximation bound for the distance between the fixed-point set of BAPG and the critical point set of GW. Moreover, under a mild technical assumption, we can show that BAPG converges to its fixed point set. The effectiveness of BAPG has been validated through comprehensive numerical experiments in graph alignment and partition tasks, where it outperforms existing methods in terms of both solution quality and wall-clock time.

Outlier-Robust Gromov Wasserstein for Graph Data

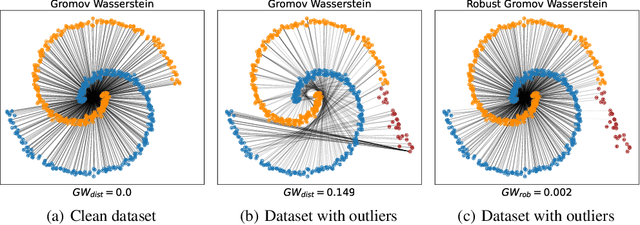
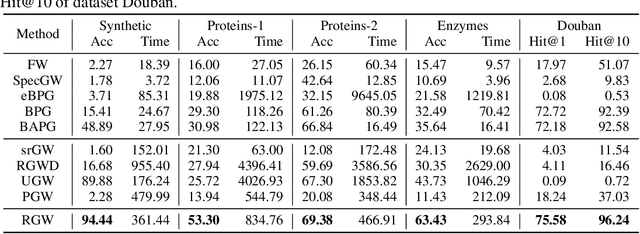
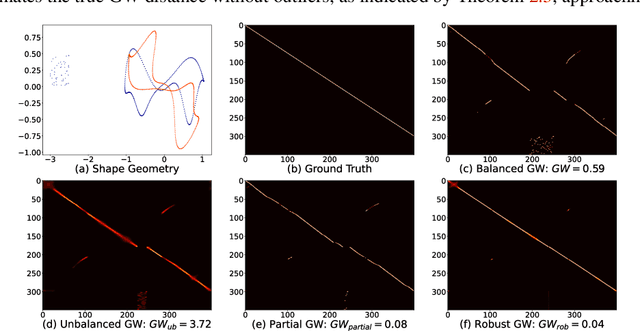
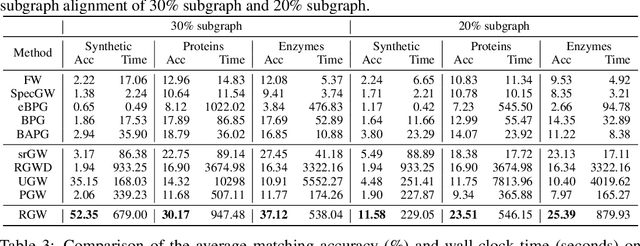
Gromov Wasserstein (GW) distance is a powerful tool for comparing and aligning probability distributions supported on different metric spaces. It has become the main modeling technique for aligning heterogeneous data for a wide range of graph learning tasks. However, the GW distance is known to be highly sensitive to outliers, which can result in large inaccuracies if the outliers are given the same weight as other samples in the objective function. To mitigate this issue, we introduce a new and robust version of the GW distance called RGW. RGW features optimistically perturbed marginal constraints within a $\varphi$-divergence based ambiguity set. To make the benefits of RGW more accessible in practice, we develop a computationally efficient algorithm, Bregman proximal alternating linearization minimization, with a theoretical convergence guarantee. Through extensive experimentation, we validate our theoretical results and demonstrate the effectiveness of RGW on real-world graph learning tasks, such as subgraph matching and partial shape correspondence.

Fast and Provably Convergent Algorithms for Gromov-Wasserstein in Graph Learning

In this paper, we study the design and analysis of a class of efficient algorithms for computing the Gromov-Wasserstein (GW) distance tailored to large-scale graph learning tasks. Armed with the Luo-Tseng error bound condition~\cite{luo1992error}, two proposed algorithms, called Bregman Alternating Projected Gradient (BAPG) and hybrid Bregman Proximal Gradient (hBPG) are proven to be (linearly) convergent. Upon task-specific properties, our analysis further provides novel theoretical insights to guide how to select the best fit method. As a result, we are able to provide comprehensive experiments to validate the effectiveness of our methods on a host of tasks, including graph alignment, graph partition, and shape matching. In terms of both wall-clock time and modeling performance, the proposed methods achieve state-of-the-art results.