Probe-Free Low-Rank Activation Intervention

Language models (LMs) can produce texts that appear accurate and coherent but contain untruthful or toxic content. Inference-time interventions that edit the hidden activations have shown promising results in steering the LMs towards desirable generations. Existing activation intervention methods often comprise an activation probe to detect undesirable generation, triggering the activation modification to steer subsequent generation. This paper proposes a probe-free intervention method FLORAIN for all attention heads in a specific activation layer. It eliminates the need to train classifiers for probing purposes. The intervention function is parametrized by a sample-wise nonlinear low-rank mapping, which is trained by minimizing the distance between the modified activations and their projection onto the manifold of desirable content. Under specific constructions of the manifold and projection distance, we show that the intervention strategy can be computed efficiently by solving a smooth optimization problem. The empirical results, benchmarked on multiple base models, demonstrate that FLORAIN consistently outperforms several baseline methods in enhancing model truthfulness and quality across generation and multiple-choice tasks.

Network Games Induced Prior for Graph Topology Learning

Learning the graph topology of a complex network is challenging due to limited data availability and imprecise data models. A common remedy in existing works is to incorporate priors such as sparsity or modularity which highlight on the structural property of graph topology. We depart from these approaches to develop priors that are directly inspired by complex network dynamics. Focusing on social networks with actions modeled by equilibriums of linear quadratic games, we postulate that the social network topologies are optimized with respect to a social welfare function. Utilizing this prior knowledge, we propose a network games induced regularizer to assist graph learning. We then formulate the graph topology learning problem as a bilevel program. We develop a two-timescale gradient algorithm to tackle the latter. We draw theoretical insights on the optimal graph structure of the bilevel program and show that they agree with the topology in several man-made networks. Empirically, we demonstrate the proposed formulation gives rise to reliable estimate of graph topology.

On subdifferential chain rule of matrix factorization and beyond

In this paper, we study equality-type Clarke subdifferential chain rules of matrix factorization and factorization machine. Specifically, we show for these problems that provided the latent dimension is larger than some multiple of the problem size (i.e., slightly overparameterized) and the loss function is locally Lipschitz, the subdifferential chain rules hold everywhere. In addition, we examine the tightness of the analysis through some interesting constructions and make some important observations from the perspective of optimization; e.g., we show that for all this type of problems, computing a stationary point is trivial. Some tensor generalizations and neural extensions are also discussed, albeit they remain mostly open.

$\ell_1$-norm rank-one symmetric matrix factorization has no spurious second-order stationary points

This paper studies the nonsmooth optimization landscape of the $\ell_1$-norm rank-one symmetric matrix factorization problem using tools from second-order variational analysis. Specifically, as the main finding of this paper, we show that any second-order stationary point (and thus local minimizer) of the problem is actually globally optimal. Besides, some other results concerning the landscape of the problem, such as a complete characterization of the set of stationary points, are also developed, which should be interesting in their own rights. Furthermore, with the above theories, we revisit existing results on the generic minimizing behavior of simple algorithms for nonsmooth optimization and showcase the potential risk of their applications to our problem through several examples. Our techniques can potentially be applied to analyze the optimization landscapes of a variety of other more sophisticated nonsmooth learning problems, such as robust low-rank matrix recovery.

Nonconvex Federated Learning on Compact Smooth Submanifolds With Heterogeneous Data

Many machine learning tasks, such as principal component analysis and low-rank matrix completion, give rise to manifold optimization problems. Although there is a large body of work studying the design and analysis of algorithms for manifold optimization in the centralized setting, there are currently very few works addressing the federated setting. In this paper, we consider nonconvex federated learning over a compact smooth submanifold in the setting of heterogeneous client data. We propose an algorithm that leverages stochastic Riemannian gradients and a manifold projection operator to improve computational efficiency, uses local updates to improve communication efficiency, and avoids client drift. Theoretically, we show that our proposed algorithm converges sub-linearly to a neighborhood of a first-order optimal solution by using a novel analysis that jointly exploits the manifold structure and properties of the loss functions. Numerical experiments demonstrate that our algorithm has significantly smaller computational and communication overhead than existing methods.

Spurious Stationarity and Hardness Results for Mirror Descent

Despite the considerable success of Bregman proximal-type algorithms, such as mirror descent, in machine learning, a critical question remains: Can existing stationarity measures, often based on Bregman divergence, reliably distinguish between stationary and non-stationary points? In this paper, we present a groundbreaking finding: All existing stationarity measures necessarily imply the existence of spurious stationary points. We further establish an algorithmic independent hardness result: Bregman proximal-type algorithms are unable to escape from a spurious stationary point in finite steps when the initial point is unfavorable, even for convex problems. Our hardness result points out the inherent distinction between Euclidean and Bregman geometries, and introduces both fundamental theoretical and numerical challenges to both machine learning and optimization communities.

Extreme Point Pursuit -- Part II: Further Error Bound Analysis and Applications

In the first part of this study, a convex-constrained penalized formulation was studied for a class of constant modulus (CM) problems. In particular, the error bound techniques were shown to play a vital role in providing exact penalization results. In this second part of the study, we continue our error bound analysis for the cases of partial permutation matrices, size-constrained assignment matrices and non-negative semi-orthogonal matrices. We develop new error bounds and penalized formulations for these three cases, and the new formulations possess good structures for building computationally efficient algorithms. Moreover, we provide numerical results to demonstrate our framework in a variety of applications such as the densest k-subgraph problem, graph matching, size-constrained clustering, non-negative orthogonal matrix factorization and sparse fair principal component analysis.

Extreme Point Pursuit -- Part I: A Framework for Constant Modulus Optimization

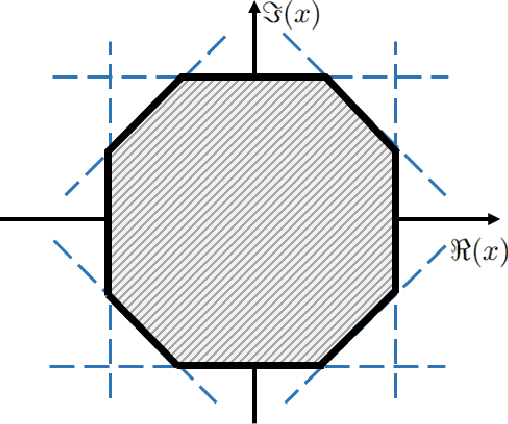
This study develops a framework for a class of constant modulus (CM) optimization problems, which covers binary constraints, discrete phase constraints, semi-orthogonal matrix constraints, non-negative semi-orthogonal matrix constraints, and several types of binary assignment constraints. Capitalizing on the basic principles of concave minimization and error bounds, we study a convex-constrained penalized formulation for general CM problems. The advantage of such formulation is that it allows us to leverage non-convex optimization techniques, such as the simple projected gradient method, to build algorithms. As the first part of this study, we explore the theory of this framework. We study conditions under which the formulation provides exact penalization results. We also examine computational aspects relating to the use of the projected gradient method for each type of CM constraint. Our study suggests that the proposed framework has a broad scope of applicability.

A Survey of Advances in Optimization Methods for Wireless Communication System Design

Mathematical optimization is now widely regarded as an indispensable modeling and solution tool for the design of wireless communications systems. While optimization has played a significant role in the revolutionary progress in wireless communication and networking technologies from 1G to 5G and onto the future 6G, the innovations in wireless technologies have also substantially transformed the nature of the underlying mathematical optimization problems upon which the system designs are based and have sparked significant innovations in the development of methodologies to understand, to analyze, and to solve those problems. In this paper, we provide a comprehensive survey of recent advances in mathematical optimization theory and algorithms for wireless communication system design. We begin by illustrating common features of mathematical optimization problems arising in wireless communication system design. We discuss various scenarios and use cases and their associated mathematical structures from an optimization perspective. We then provide an overview of recent advances in mathematical optimization theory and algorithms, from nonconvex optimization, global optimization, and integer programming, to distributed optimization and learning-based optimization. The key to successful solution of mathematical optimization problems is in carefully choosing and/or developing suitable optimization algorithms (or neural network architectures) that can exploit the underlying problem structure. We conclude the paper by identifying several open research challenges and outlining future research directions.

On the Estimation Performance of Generalized Power Method for Heteroscedastic Probabilistic PCA

The heteroscedastic probabilistic principal component analysis (PCA) technique, a variant of the classic PCA that considers data heterogeneity, is receiving more and more attention in the data science and signal processing communities. In this paper, to estimate the underlying low-dimensional linear subspace (simply called \emph{ground truth}) from available heterogeneous data samples, we consider the associated non-convex maximum-likelihood estimation problem, which involves maximizing a sum of heterogeneous quadratic forms over an orthogonality constraint (HQPOC). We propose a first-order method -- generalized power method (GPM) -- to tackle the problem and establish its \emph{estimation performance} guarantee. Specifically, we show that, given a suitable initialization, the distances between the iterates generated by GPM and the ground truth decrease at least geometrically to some threshold associated with the residual part of certain "population-residual decomposition". In establishing the estimation performance result, we prove a novel local error bound property of another closely related optimization problem, namely quadratic optimization with orthogonality constraint (QPOC), which is new and can be of independent interest. Numerical experiments are conducted to demonstrate the superior performance of GPM in both Gaussian noise and sub-Gaussian noise settings.