Ya Liu
A Scalable and Exact Relaxation for Densest $k$-Subgraph via Error Bounds
Nov 17, 2025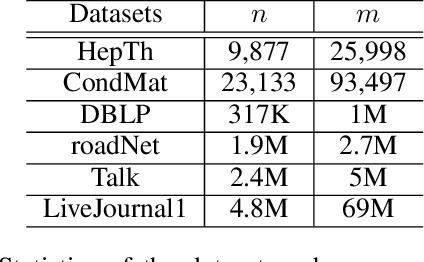
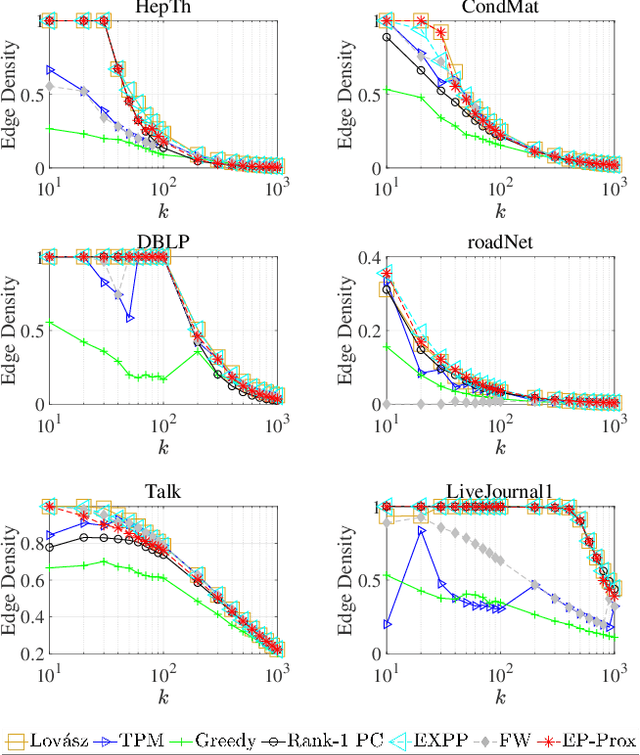
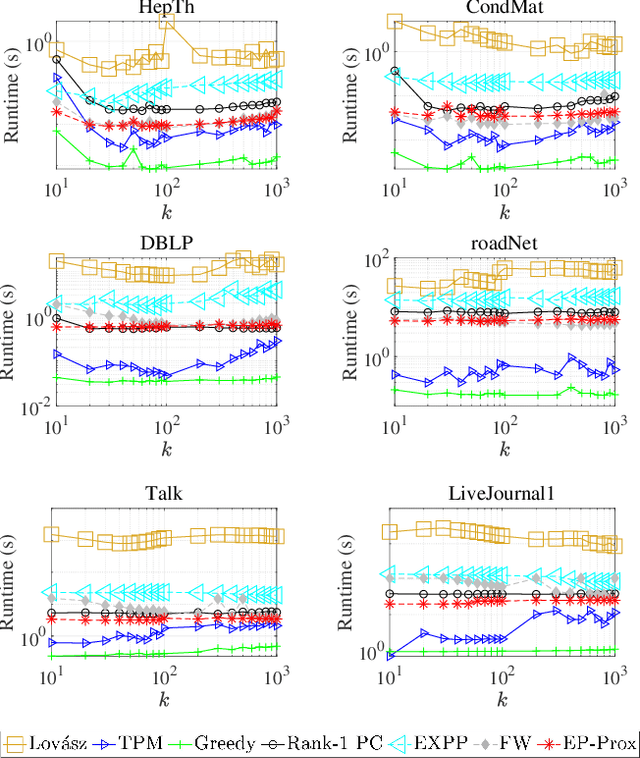
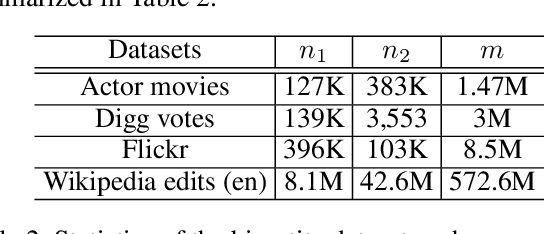
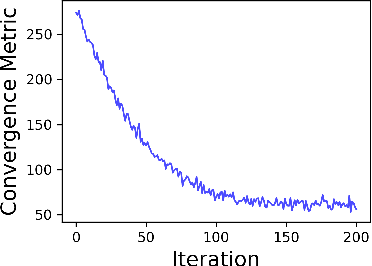
Abstract:Given an undirected graph and a size parameter $k$, the Densest $k$-Subgraph (D$k$S) problem extracts the subgraph on $k$ vertices with the largest number of induced edges. While D$k$S is NP--hard and difficult to approximate, penalty-based continuous relaxations of the problem have recently enjoyed practical success for real-world instances of D$k$S. In this work, we propose a scalable and exact continuous penalization approach for D$k$S using the error bound principle, which enables the design of suitable penalty functions. Notably, we develop new theoretical guarantees ensuring that both the global and local optima of the penalized problem match those of the original problem. The proposed penalized reformulation enables the use of first-order continuous optimization methods. In particular, we develop a non-convex proximal gradient algorithm, where the non-convex proximal operator can be computed in closed form, resulting in low per-iteration complexity. We also provide convergence analysis of the algorithm. Experiments on large-scale instances of the D$k$S problem and one of its variants, the Densest ($k_1, k_2$) Bipartite Subgraph (D$k_1k_2$BS) problem, demonstrate that our method achieves a favorable balance between computation cost and solution quality.
DEKC: Data-Enable Control for Tethered Space Robot Deployment in the Presence of Uncertainty via Koopman Operator Theory
Jun 10, 2025Abstract:This work focuses the deployment of tethered space robot in the presence of unknown uncertainty. A data-enable framework called DEKC which contains offline training part and online execution part is proposed to deploy tethered space robot in the presence of uncertainty. The main idea of this work is modeling the unknown uncertainty as a dynamical system, which enables high accuracy and convergence of capturing uncertainty. The core part of proposed framework is a proxy model of uncertainty, which is derived from data-driven Koopman theory and is separated with controller design. In the offline stage, the lifting functions associated with Koopman operator are parameterized with deep neural networks. Then by solving an optimization problem, the lifting functions are learned from sampling data. In the online execution stage, the proxy model cooperates the learned lifting functions obtained in the offline phase to capture the unknown uncertainty. Then the output of proxy model is compensated to the baseline controller such that the effect of uncertainty can be attenuated or even eliminated. Furthermore, considering some scenarios in which the performance of proxy model may weaken, a receding-horizon scheme is proposed to update the proxy model online. Finally, the extensive numerical simulations demonstrate the effectiveness of our proposed framework. The implementation of proposed DEKC framework is publicly available at https://github.com/NPU-RCIR/DEKC.git.
Argus: Federated Non-convex Bilevel Learning over 6G Space-Air-Ground Integrated Network
May 14, 2025
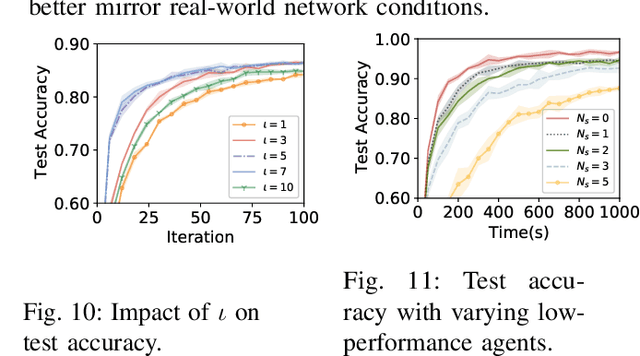

Abstract:The space-air-ground integrated network (SAGIN) has recently emerged as a core element in the 6G networks. However, traditional centralized and synchronous optimization algorithms are unsuitable for SAGIN due to infrastructureless and time-varying environments. This paper aims to develop a novel Asynchronous algorithm a.k.a. Argus for tackling non-convex and non-smooth decentralized federated bilevel learning over SAGIN. The proposed algorithm allows networked agents (e.g. autonomous aerial vehicles) to tackle bilevel learning problems in time-varying networks asynchronously, thereby averting stragglers from impeding the overall training speed. We provide a theoretical analysis of the iteration complexity, communication complexity, and computational complexity of Argus. Its effectiveness is further demonstrated through numerical experiments.
Neural Predictor for Flight Control with Payload
Oct 21, 2024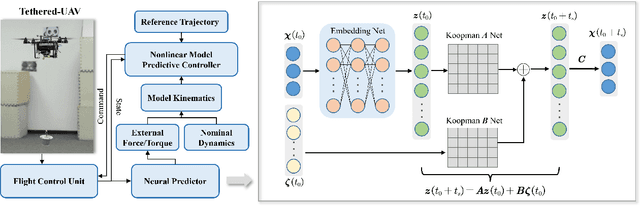
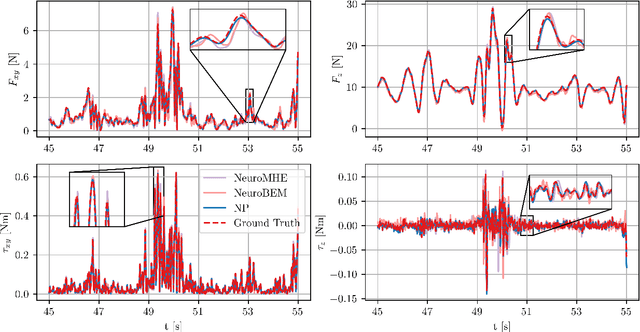

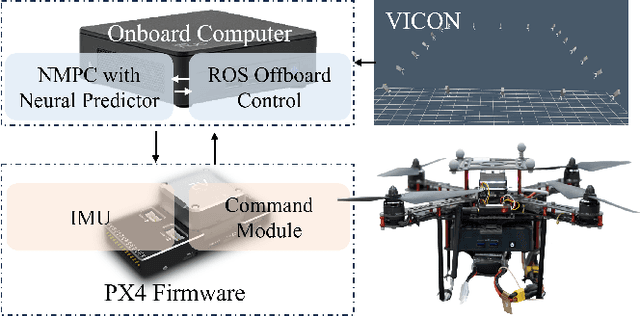
Abstract:Aerial robotics for transporting suspended payloads as the form of freely-floating manipulator are growing great interest in recent years. However, the prior information of the payload, such as the mass, is always hard to obtain accurately in practice. The force/torque caused by payload and residual dynamics will introduce unmodeled perturbations to the system, which negatively affects the closed-loop performance. Different from estimation-like methods, this paper proposes Neural Predictor, a learning-based approach to model force/torque caused by payload and residual dynamics as a dynamical system. It results a hybrid model including both the first-principles dynamics and the learned dynamics. This hybrid model is then integrated into a MPC framework to improve closed-loop performance. Effectiveness of proposed framework is verified extensively in both numerical simulations and real-world flight experiments. The results indicate that our approach can capture force/torque caused by payload and residual dynamics accurately, respond quickly to the changes of them and improve the closed-loop performance significantly. In particular, Neural Predictor outperforms a state-of-the-art learning-based estimator and has reduced the force and torque estimation errors by up to 66.15% and 33.33% while using less samples.
Extreme Point Pursuit -- Part I: A Framework for Constant Modulus Optimization
Mar 11, 2024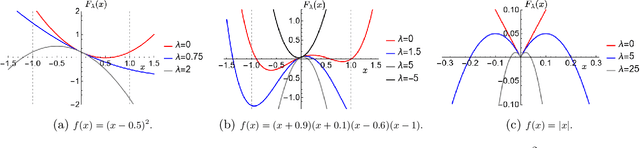
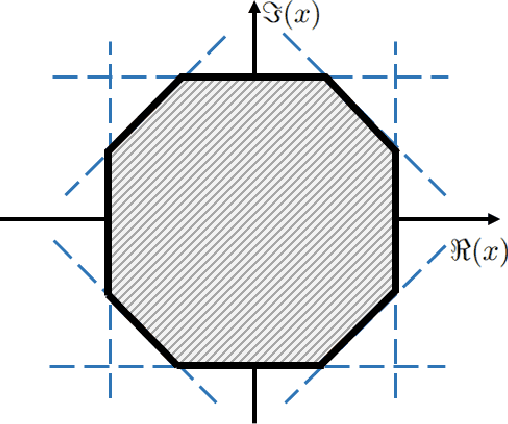
Abstract:This study develops a framework for a class of constant modulus (CM) optimization problems, which covers binary constraints, discrete phase constraints, semi-orthogonal matrix constraints, non-negative semi-orthogonal matrix constraints, and several types of binary assignment constraints. Capitalizing on the basic principles of concave minimization and error bounds, we study a convex-constrained penalized formulation for general CM problems. The advantage of such formulation is that it allows us to leverage non-convex optimization techniques, such as the simple projected gradient method, to build algorithms. As the first part of this study, we explore the theory of this framework. We study conditions under which the formulation provides exact penalization results. We also examine computational aspects relating to the use of the projected gradient method for each type of CM constraint. Our study suggests that the proposed framework has a broad scope of applicability.
Extreme Point Pursuit -- Part II: Further Error Bound Analysis and Applications
Mar 11, 2024Abstract:In the first part of this study, a convex-constrained penalized formulation was studied for a class of constant modulus (CM) problems. In particular, the error bound techniques were shown to play a vital role in providing exact penalization results. In this second part of the study, we continue our error bound analysis for the cases of partial permutation matrices, size-constrained assignment matrices and non-negative semi-orthogonal matrices. We develop new error bounds and penalized formulations for these three cases, and the new formulations possess good structures for building computationally efficient algorithms. Moreover, we provide numerical results to demonstrate our framework in a variety of applications such as the densest k-subgraph problem, graph matching, size-constrained clustering, non-negative orthogonal matrix factorization and sparse fair principal component analysis.
Unsupervised Deep Learning for IoT Time Series
Feb 21, 2023



Abstract:IoT time series analysis has found numerous applications in a wide variety of areas, ranging from health informatics to network security. Nevertheless, the complex spatial temporal dynamics and high dimensionality of IoT time series make the analysis increasingly challenging. In recent years, the powerful feature extraction and representation learning capabilities of deep learning (DL) have provided an effective means for IoT time series analysis. However, few existing surveys on time series have systematically discussed unsupervised DL-based methods. To fill this void, we investigate unsupervised deep learning for IoT time series, i.e., unsupervised anomaly detection and clustering, under a unified framework. We also discuss the application scenarios, public datasets, existing challenges, and future research directions in this area.
* 22 pages, 8 figures, has been published by IEEE Internet of Things Journal
A Unified Cognitive Learning Framework for Adapting to Dynamic Environment and Tasks
Jun 01, 2021



Abstract:Many machine learning frameworks have been proposed and used in wireless communications for realizing diverse goals. However, their incapability of adapting to the dynamic wireless environment and tasks and of self-learning limit their extensive applications and achievable performance. Inspired by the great flexibility and adaptation of primate behaviors due to the brain cognitive mechanism, a unified cognitive learning (CL) framework is proposed for the dynamic wireless environment and tasks. The mathematical framework for our proposed CL is established. Using the public and authoritative dataset, we demonstrate that our proposed CL framework has three advantages, namely, the capability of adapting to the dynamic environment and tasks, the self-learning capability and the capability of 'good money driving out bad money' by taking modulation recognition as an example. The proposed CL framework can enrich the current learning frameworks and widen the applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge