Wing-Kin Ma
A Scalable and Exact Relaxation for Densest $k$-Subgraph via Error Bounds
Nov 17, 2025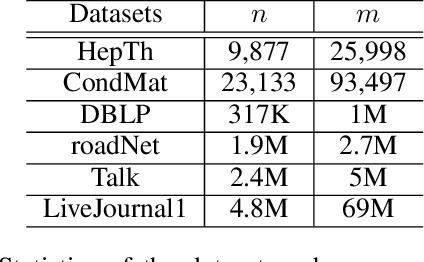
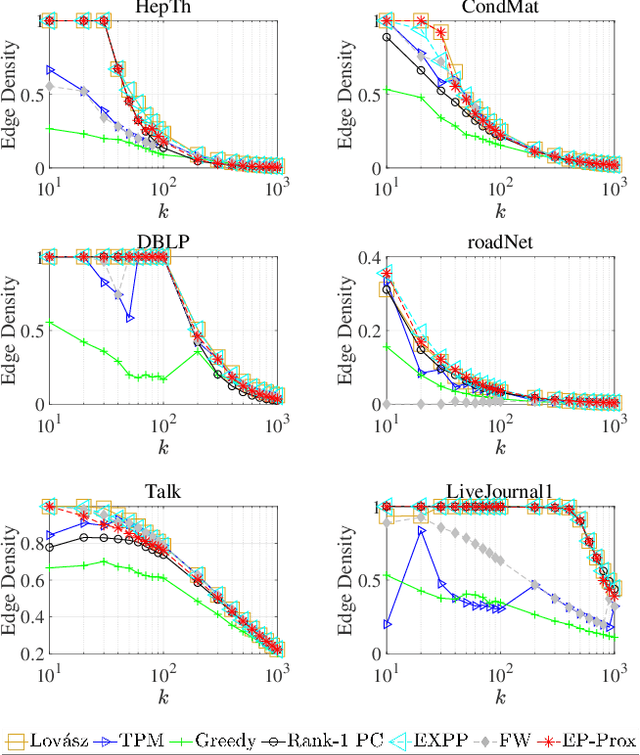
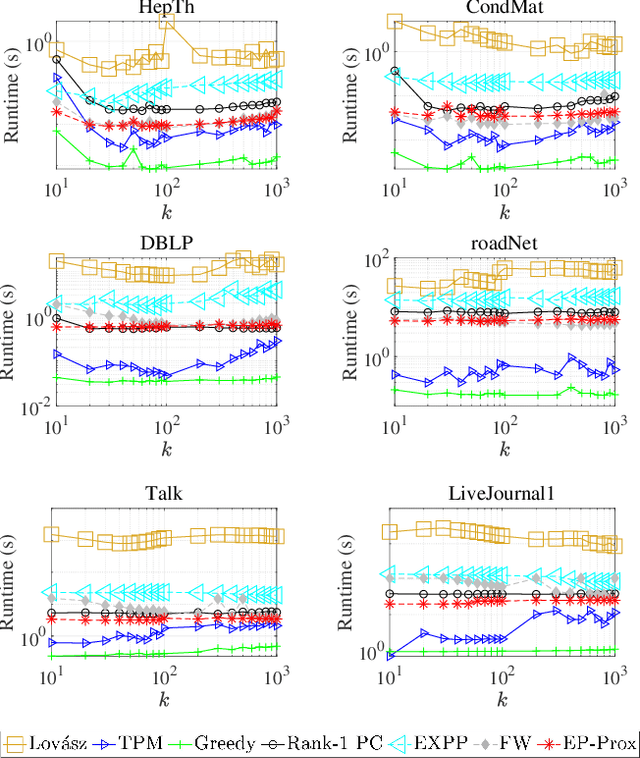
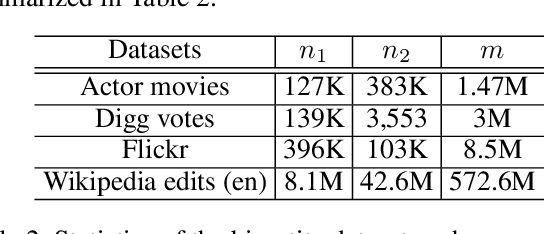
Abstract:Given an undirected graph and a size parameter $k$, the Densest $k$-Subgraph (D$k$S) problem extracts the subgraph on $k$ vertices with the largest number of induced edges. While D$k$S is NP--hard and difficult to approximate, penalty-based continuous relaxations of the problem have recently enjoyed practical success for real-world instances of D$k$S. In this work, we propose a scalable and exact continuous penalization approach for D$k$S using the error bound principle, which enables the design of suitable penalty functions. Notably, we develop new theoretical guarantees ensuring that both the global and local optima of the penalized problem match those of the original problem. The proposed penalized reformulation enables the use of first-order continuous optimization methods. In particular, we develop a non-convex proximal gradient algorithm, where the non-convex proximal operator can be computed in closed form, resulting in low per-iteration complexity. We also provide convergence analysis of the algorithm. Experiments on large-scale instances of the D$k$S problem and one of its variants, the Densest ($k_1, k_2$) Bipartite Subgraph (D$k_1k_2$BS) problem, demonstrate that our method achieves a favorable balance between computation cost and solution quality.
One-Bit Sigma-Delta DFRC Waveform Design: Using Quantization Noise for Radar Probing
Jan 27, 2025



Abstract:Dual-functional radar-communication (DFRC) signal design has received much attention lately. We consider the scenario of one-bit massive multi-input multi-output (MIMO) wherein one-bit DACs are employed for the sake of saving hardware costs. Specifically, a spatial Sigma-Delta $(\Sigma\Delta)$ modulation scheme is proposed for one-bit MIMO-DFRC waveform design. Unlike the existing approaches which require large-scale binary optimization, the proposed scheme performs $\Sigma\Delta$ modulation on a continuous-valued DFRC signal. The subsequent waveform design is formulated as a constrained least square problem, which can be efficiently solved. Moreover, we leverage quantization noise for radar probing purposes, rather than treating it as unwanted noise. Numerical results demonstrate that the proposed scheme performs well in both radar probing and downlink precoding.
Downlink MIMO Channel Estimation from Bits: Recoverability and Algorithm
Nov 25, 2024



Abstract:In frequency division duplex (FDD) massive MIMO systems, a major challenge lies in acquiring the downlink channel state information}\ (CSI) at the base station (BS) from limited feedback sent by the user equipment (UE). To tackle this fundamental task, our contribution is twofold: First, a simple feedback framework is proposed, where a compression and Gaussian dithering-based quantization strategy is adopted at the UE side, and then a maximum likelihood estimator (MLE) is formulated at the BS side. Recoverability of the MIMO channel under the widely used double directional model is established. Specifically, analyses are presented for two compression schemes -- showing one being more overhead-economical and the other computationally lighter at the UE side. Second, to realize the MLE, an alternating direction method of multipliers (ADMM) algorithm is proposed. The algorithm is carefully designed to integrate a sophisticated harmonic retrieval (HR) solver as subroutine, which turns out to be the key of effectively tackling this hard MLE problem.Extensive numerical experiments are conducted to validate the efficacy of our approach.
Hyperspectral Unmixing Under Endmember Variability: A Variational Inference Framework
Jul 20, 2024



Abstract:This work proposes a variational inference (VI) framework for hyperspectral unmixing in the presence of endmember variability (HU-EV). An EV-accounted noisy linear mixture model (LMM) is considered, and the presence of outliers is also incorporated into the model. Following the marginalized maximum likelihood (MML) principle, a VI algorithmic structure is designed for probabilistic inference for HU-EV. Specifically, a patch-wise static endmember assumption is employed to exploit spatial smoothness and to try to overcome the ill-posed nature of the HU-EV problem. The design facilitates lightweight, continuous optimization-based updates under a variety of endmember priors. Some of the priors, such as the Beta prior, were previously used under computationally heavy, sampling-based probabilistic HU-EV methods. The effectiveness of the proposed framework is demonstrated through synthetic, semi-real, and real-data experiments.
One-Bit MIMO Detection: From Global Maximum-Likelihood Detector to Amplitude Retrieval Approach
Jul 13, 2024Abstract:As communication systems advance towards the future 6G era, the incorporation of large-scale antenna arrays in base stations (BSs) presents challenges such as increased hardware costs and energy consumption. To address these issues, the use of one-bit analog-to-digital converters (ADCs)/digital-to-analog converters (DACs) has gained significant attentions. This paper focuses on one-bit multiple-input multiple-output (MIMO) detection in an uplink multiuser transmission scenario where the BS employs one-bit ADCs. One-bit quantization retains only the sign information and loses the amplitude information, which poses a unique challenge in the corresponding detection problem. The maximum-likelihood (ML) formulation of one-bit MIMO detection has a challenging likelihood function that hinders the application of many high-performance detectors developed for classic MIMO detection (under high-resolution ADCs). While many approximate methods for the ML detection problem have been studied, it lacks an efficient global algorithm. This paper fills this gap by proposing an efficient branch-and-bound algorithm, which is guaranteed to find the global solution of the one-bit ML MIMO detection problem. Additionally, a new amplitude retrieval (AR) detection approach is developed, incorporating explicit amplitude variables into the problem formulation. The AR approach yields simpler objective functions that enable the development of efficient algorithms offering both global and approximate solutions. The paper also contributes to the computational complexity analysis of both ML and AR detection problems. Extensive simulations are conducted to demonstrate the effectiveness and efficiency of the proposed formulations and algorithms.
Extreme Point Pursuit -- Part I: A Framework for Constant Modulus Optimization
Mar 11, 2024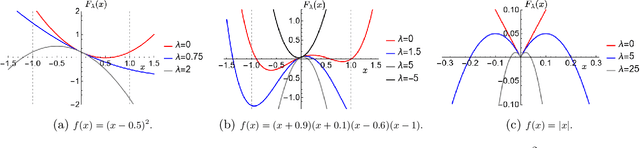
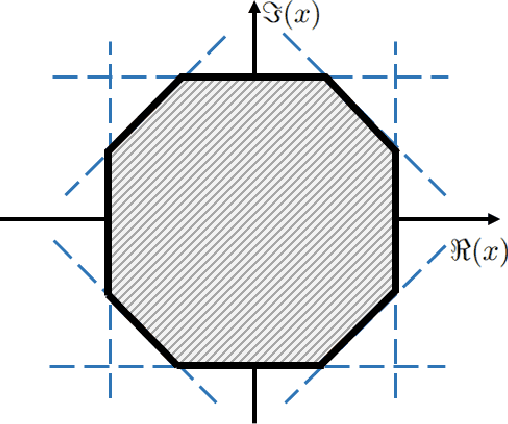
Abstract:This study develops a framework for a class of constant modulus (CM) optimization problems, which covers binary constraints, discrete phase constraints, semi-orthogonal matrix constraints, non-negative semi-orthogonal matrix constraints, and several types of binary assignment constraints. Capitalizing on the basic principles of concave minimization and error bounds, we study a convex-constrained penalized formulation for general CM problems. The advantage of such formulation is that it allows us to leverage non-convex optimization techniques, such as the simple projected gradient method, to build algorithms. As the first part of this study, we explore the theory of this framework. We study conditions under which the formulation provides exact penalization results. We also examine computational aspects relating to the use of the projected gradient method for each type of CM constraint. Our study suggests that the proposed framework has a broad scope of applicability.
Extreme Point Pursuit -- Part II: Further Error Bound Analysis and Applications
Mar 11, 2024Abstract:In the first part of this study, a convex-constrained penalized formulation was studied for a class of constant modulus (CM) problems. In particular, the error bound techniques were shown to play a vital role in providing exact penalization results. In this second part of the study, we continue our error bound analysis for the cases of partial permutation matrices, size-constrained assignment matrices and non-negative semi-orthogonal matrices. We develop new error bounds and penalized formulations for these three cases, and the new formulations possess good structures for building computationally efficient algorithms. Moreover, we provide numerical results to demonstrate our framework in a variety of applications such as the densest k-subgraph problem, graph matching, size-constrained clustering, non-negative orthogonal matrix factorization and sparse fair principal component analysis.
Multilayer Simplex-structured Matrix Factorization for Hyperspectral Unmixing with Endmember Variability
Jan 26, 2024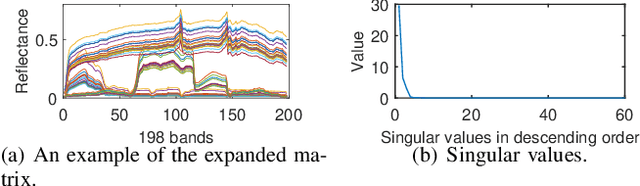
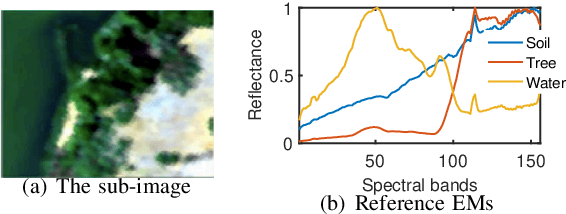
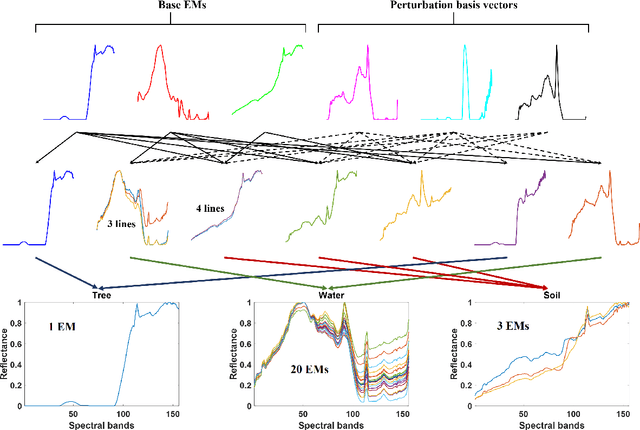
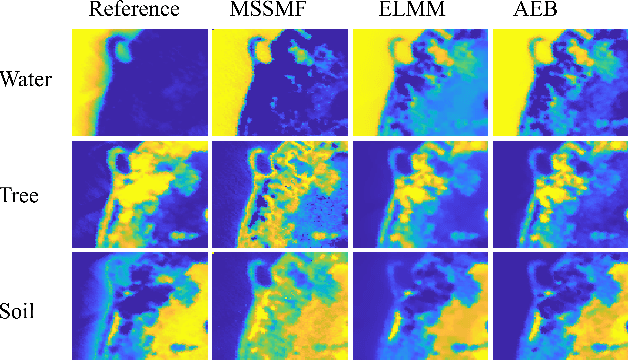
Abstract:Given a hyperspectral image, the problem of hyperspectral unmixing (HU) is to identify the endmembers (or materials) and the abundance (or endmembers' contributions on pixels) that underlie the image. HU can be seen as a matrix factorization problem with a simplex structure in the abundance matrix factor. In practice, hyperspectral images may exhibit endmember variability (EV) effects -- the endmember matrix factor varies from one pixel to another. In this paper we consider a multilayer simplex-structured matrix factorization model to account for the EV effects. Our multilayer model is based on the postulate that if we arrange the varied endmembers as an expanded endmember matrix, that matrix exhibits a low-rank structure. A variational inference-based maximum-likelihood estimation method is employed to tackle the multilayer factorization problem. Simulation results are provided to demonstrate the performance of our multilayer factorization method.
Transmitting Data Through Reconfigurable Intelligent Surface: A Spatial Sigma-Delta Modulation Approach
Oct 25, 2023



Abstract:Transmitting data using the phases on reconfigurable intelligent surfaces (RIS) is a promising solution for future energy-efficient communication systems. Recent work showed that a virtual phased massive multiuser multiple-input-multiple-out (MIMO) transmitter can be formed using only one active antenna and a large passive RIS. In this paper, we are interested in using such a system to perform MIMO downlink precoding. In this context, we may not be able to apply conventional MIMO precoding schemes, such as the simple zero-forcing (ZF) scheme, and we typically need to design the phase signals by solving optimization problems with constant modulus constraints or with discrete phase constraints, which pose challenges with high computational complexities. In this work, we propose an alternative approach based on Sigma-Delta ($\Sigma\Delta$) modulation, which is classically famous for its noise-shaping ability. Specifically, first-order $\Sigma\Delta$ modulation is applied in the spatial domain to handle phase quantization in generating constant envelope signals. Under some mild assumptions, the proposed phased $\Sigma\Delta$ modulator allows us to use the ZF scheme to synthesize the RIS reflection phases with negligible complexity. The proposed approach is empirically shown to achieve comparable bit error rate performance to the unquantized ZF scheme.
Spatial Sigma-Delta Modulation for Coarsely Quantized Massive MIMO Downlink: Flexible Designs by Convex Optimization
Oct 22, 2023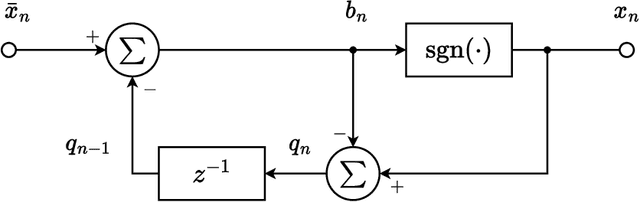
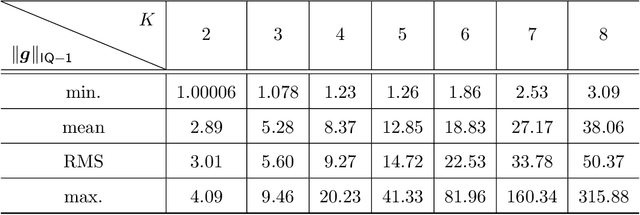
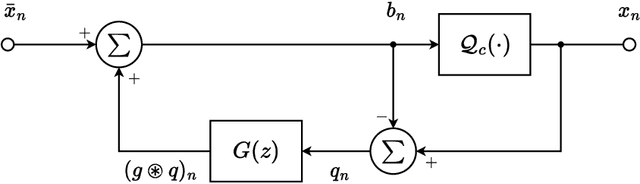
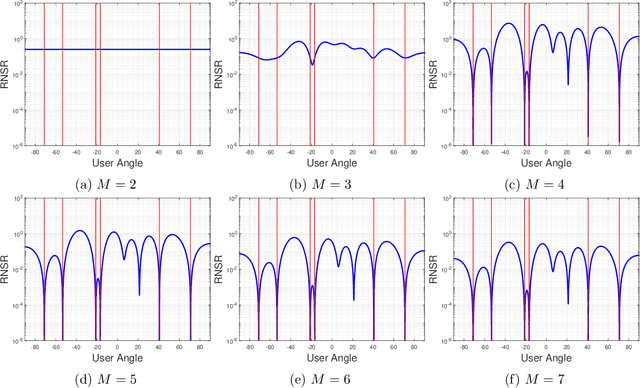
Abstract:This paper considers the context of multiuser massive MIMO downlink precoding with low-resolution digital-to-analog converters (DACs) at the transmitter. This subject is motivated by the consideration that it is expensive to employ high-resolution DACs for practical massive MIMO implementations. The challenge with using low-resolution DACs is to overcome the detrimental quantization error effects. Recently, spatial Sigma-Delta modulation has arisen as a viable way to put quantization errors under control. This approach takes insight from temporal Sigma-Delta modulation in classical DAC studies. Assuming a 1D uniform linear transmit antenna array, the principle is to shape the quantization errors in space such that the shaped quantization errors are pushed away from the user-serving angle sector. In the previous studies, spatial Sigma-Delta modulation was performed by direct application of the basic first- and second-order modulators from the Sigma-Delta literature. In this paper, we develop a general Sigma-Delta modulator design framework for any given order, for any given number of quantization levels, and for any given angle sector. We formulate our design as a problem of maximizing the signal-to-quantization-and-noise ratios experienced by the users. The formulated problem is convex and can be efficiently solved by available solvers. Our proposed framework offers the alternative option of focused quantization error suppression in accordance with channel state information. Our framework can also be extended to 2D planar transmit antenna arrays. We perform numerical study under different operating conditions, and the numerical results suggest that, given a moderate number of quantization levels, say, 5 to 7 levels, our optimization-based Sigma-Delta modulation schemes can lead to bit error rate performance close to that of the unquantized counterpart.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge