QoS-Aware and Routing-Flexible Network Slicing for Service-Oriented Networks

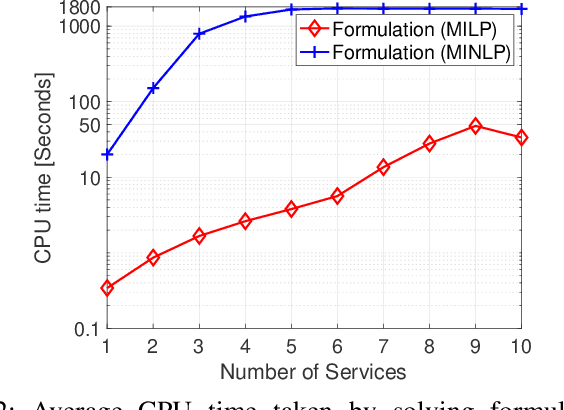
In this paper, we consider the network slicing (NS) problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and manage network resources to meet diverse quality of service (QoS) requirements. We propose a mixed-integer nonlinear programming (MINLP) formulation for the considered NS problem that can flexibly route the traffic flow of the services on multiple paths and provide end-to-end delay and reliability guarantees for all services. To overcome the computational difficulty due to the intrinsic nonlinearity in the MINLP formulation, we transform the MINLP formulation into an equivalent mixed-integer linear programming (MILP) formulation and further show that their continuous relaxations are equivalent. In sharp contrast to the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial-time solvable linear programming problem, which significantly facilitates the algorithmic design. Based on the newly proposed MILP formulation, we develop a customized column generation (cCG) algorithm for solving the NS problem. The proposed cCG algorithm is a decomposition-based algorithm and is particularly suitable for solving large-scale NS problems. Numerical results demonstrate the efficacy of the proposed formulations and the proposed cCG algorithm.

One-Bit MIMO Detection: From Global Maximum-Likelihood Detector to Amplitude Retrieval Approach

As communication systems advance towards the future 6G era, the incorporation of large-scale antenna arrays in base stations (BSs) presents challenges such as increased hardware costs and energy consumption. To address these issues, the use of one-bit analog-to-digital converters (ADCs)/digital-to-analog converters (DACs) has gained significant attentions. This paper focuses on one-bit multiple-input multiple-output (MIMO) detection in an uplink multiuser transmission scenario where the BS employs one-bit ADCs. One-bit quantization retains only the sign information and loses the amplitude information, which poses a unique challenge in the corresponding detection problem. The maximum-likelihood (ML) formulation of one-bit MIMO detection has a challenging likelihood function that hinders the application of many high-performance detectors developed for classic MIMO detection (under high-resolution ADCs). While many approximate methods for the ML detection problem have been studied, it lacks an efficient global algorithm. This paper fills this gap by proposing an efficient branch-and-bound algorithm, which is guaranteed to find the global solution of the one-bit ML MIMO detection problem. Additionally, a new amplitude retrieval (AR) detection approach is developed, incorporating explicit amplitude variables into the problem formulation. The AR approach yields simpler objective functions that enable the development of efficient algorithms offering both global and approximate solutions. The paper also contributes to the computational complexity analysis of both ML and AR detection problems. Extensive simulations are conducted to demonstrate the effectiveness and efficiency of the proposed formulations and algorithms.

Quantized Constant-Envelope Waveform Design for Massive MIMO DFRC Systems

Both dual-functional radar-communication (DFRC) and massive multiple-input multiple-output (MIMO) have been recognized as enabling technologies for 6G wireless networks. This paper considers the advanced waveform design for hardware-efficient massive MIMO DFRC systems. Specifically, the transmit waveform is imposed with the quantized constant-envelope (QCE) constraint, which facilitates the employment of low-resolution digital-to-analog converters (DACs) and power-efficient amplifiers. The waveform design problem is formulated as the minimization of the mean square error (MSE) between the designed and desired beampatterns subject to the constructive interference (CI)-based communication quality of service (QoS) constraints and the QCE constraint. To solve the formulated problem, we first utilize the penalty technique to transform the discrete problem into an equivalent continuous penalty model. Then, we propose an inexact augmented Lagrangian method (ALM) algorithm for solving the penalty model. In particular, the ALM subproblem at each iteration is solved by a custom-built block successive upper-bound minimization (BSUM) algorithm, which admits closed-form updates, making the proposed inexact ALM algorithm computationally efficient. Simulation results demonstrate the superiority of the proposed approach over existing state-of-the-art ones. In addition, extensive simulations are conducted to examine the impact of various system parameters on the trade-off between communication and radar performances.

An Efficient Global Algorithm for One-Bit Maximum-Likelihood MIMO Detection

There has been growing interest in implementing massive MIMO systems by one-bit analog-to-digital converters (ADCs), which have the benefit of reducing the power consumption and hardware complexity. One-bit MIMO detection arises in such a scenario. It aims to detect the multiuser signals from the one-bit quantized received signals in an uplink channel. In this paper, we consider one-bit maximum-likelihood (ML) MIMO detection in massive MIMO systems, which amounts to solving a large-scale nonlinear integer programming problem. We propose an efficient global algorithm for solving the one-bit ML MIMO detection problem. We first reformulate the problem as a mixed integer linear programming (MILP) problem that has a massive number of linear constraints. The massive number of linear constraints raises computational challenges. To solve the MILP problem efficiently, we custom build a light-weight branch-and-bound tree search algorithm, where the linear constraints are incrementally added during the tree search procedure and only small-size linear programming subproblems need to be solved at each iteration. We provide simulation results to demonstrate the efficiency of the proposed method.

An Efficient Decomposition Algorithm for Large-Scale Network Slicing

In this paper, we consider the network slicing (NS) problem which attempts to map multiple customized virtual network requests to a common shared network infrastructure and allocate network resources to meet diverse service requirements. We propose an efficient decomposition algorithm for solving this NP-hard problem. The proposed algorithm decomposes the large-scale hard NS problem into two relatively easy function placement (FP) and traffic routing (TR) subproblems and iteratively solves them enabling information feedback between each other, which makes it particularly suitable to solve large-scale problems. Specifically, the FP subproblem is to place service functions into cloud nodes in the network, and solving it can return a function placement strategy based on which the TR subproblem is defined; and the TR subproblem is to find paths connecting two nodes hosting two adjacent functions in the network, and solving it can either verify that the solution of the FP subproblem is an optimal solution of the original problem, or return a valid inequality to the FP subproblem that cuts off the current infeasible solution. The proposed algorithm is guaranteed to find the global solution of the NS problem. We demonstrate the effectiveness and efficiency of the proposed algorithm via numerical experiments.

Diversity Order Analysis for Quantized Constant Envelope Transmission

Quantized constant envelope (QCE) transmission is a popular and effective technique to reduce the hardware cost and improve the power efficiency of 5G and beyond systems equipped with large antenna arrays. It has been widely observed that the number of quantization levels has a substantial impact on the system performance. This paper aims to quantify the impact of the number of quantization levels on the system performance. Specifically, we consider a downlink single-user multiple-input-single-output (MISO) system with M-phase shift keying (PSK) constellation under the Rayleigh fading channel. We first derive a novel bound on the system symbol error probability (SEP). Based on the derived SEP bound, we characterize the achievable diversity order of the quantized matched filter (MF) precoding strategy. Our results show that full diversity order can be achieved when the number of quantization levels L is greater than the PSK constellation order M, i.e., L>M, only half diversity order is achievable when L=M, and the achievable diversity order is 0 when L<M. Simulation results verify our theoretical analysis.

Optimal QoS-Aware Network Slicing for Service-Oriented Networks with Flexible Routing

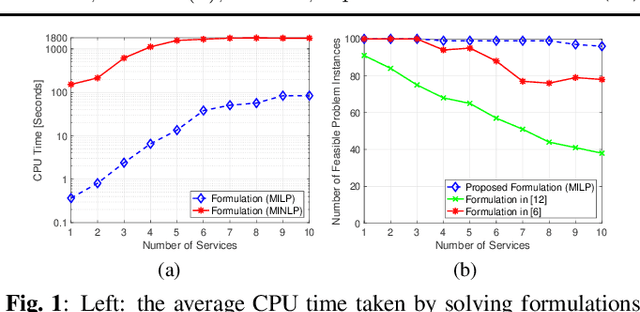
In this paper, we consider the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse quality of service (QoS) requirements. We first propose a mixed integer nonlinear program (MINLP) formulation for this problem that optimizes the network resource consumption while jointly considers QoS requirements, flow routing, and resource budget constraints. In particular, the proposed formulation is able to flexibly route the traffic flow of the services on multiple paths and provide end-to-end (E2E) delay and reliability guarantees for all services. Due to the intrinsic nonlinearity, the MINLP formulation is computationally difficult to solve. To overcome this difficulty, we then propose a mixed integer linear program (MILP) formulation and show that the two formulations and their continuous relaxations are equivalent. Different from the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial time solvable linear programming problem, which makes the MILP formulation much more computationally solvable. Numerical results demonstrate the effectiveness and efficiency of the proposed formulations over existing ones.

Towards Efficient Large-Scale Network Slicing: An LP Rounding-and-Refinement Approach

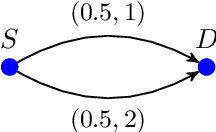
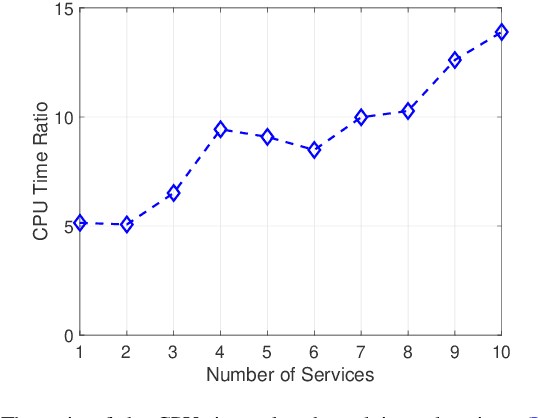
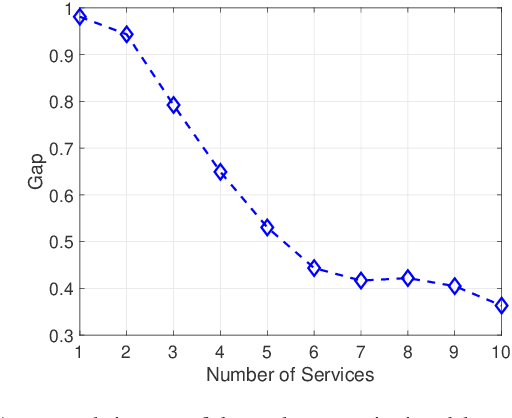
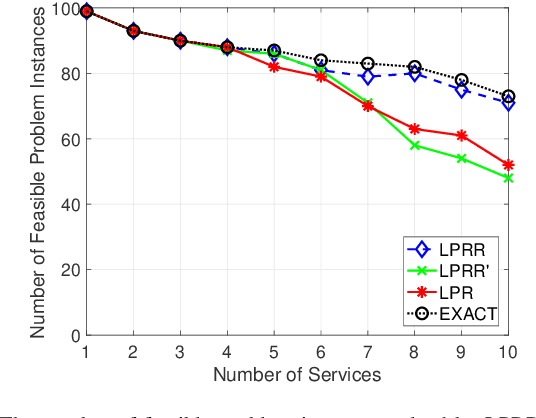
In this paper, we propose an efficient algorithm for the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse service requirements. The problem has been formulated as a mixed integer linear programming (MILP) formulation in the literature. By exploiting the special structure of the network slicing problem, we first propose a novel linear programming (LP) relaxation of the MILP formulation. We show that compared with a natural LP relaxation of the MILP formulation, the novel LP relaxation is much more compact in terms of smaller numbers of variables and constraints, and much stronger in terms of providing a better LP bound, which makes it particularly suitable to be embedded in an LP based algorithm. Then we design an efficient two-stage LP rounding-and-refinement algorithm based on this novel LP relaxation. In the first stage, the proposed algorithm uses an iterative LP rounding procedure to place the virtual network functions of all services into cloud nodes while taking traffic routing of all services into consideration; in the second stage, the proposed algorithm uses an iterative LP refinement procedure to obtain a solution for traffic routing of all services with their end-to-end delay constraints being satisfied. Compared with the existing algorithms which either have an exponential complexity or return a low-quality solution, our proposed algorithm achieves a better trade-off between the solution quality and the computational complexity. In particular, the worst-case complexity of our proposed algorithm is polynomial, which makes it suitable for solving large-scale problems. Numerical results demonstrate the effectiveness and efficiency of our proposed algorithm.

An efficient linear programming rounding-and-refinement algorithm for large-scale network slicing problem

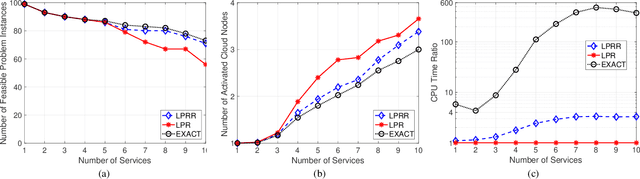
In this paper, we consider the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse service requirements, and propose an efficient two-stage algorithm for solving this NP-hard problem. In the first stage, the proposed algorithm uses an iterative linear programming (LP) rounding procedure to place the virtual network functions of all services into cloud nodes while taking traffic routing of all services into consideration; in the second stage, the proposed algorithm uses an iterative LP refinement procedure to obtain a solution for traffic routing of all services with their end-to-end delay constraints being satisfied. Compared with the existing algorithms which either have an exponential complexity or return a low-quality solution, our proposed algorithm achieves a better trade-off between solution quality and computational complexity. In particular, the worst-case complexity of our proposed algorithm is polynomial, which makes it suitable for solving large-scale problems. Numerical results demonstrate the effectiveness and efficiency of our proposed algorithm.