QoS-Aware and Routing-Flexible Network Slicing for Service-Oriented Networks
Paper and Code
Sep 20, 2024

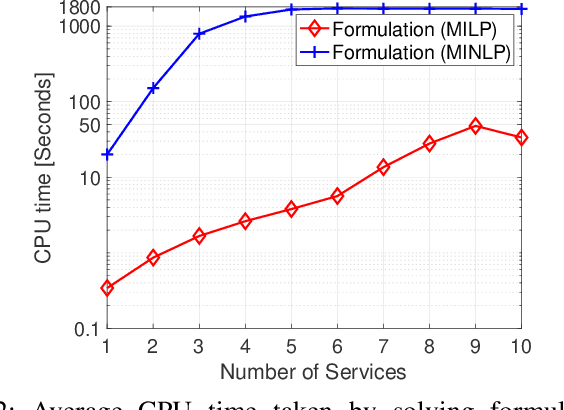

In this paper, we consider the network slicing (NS) problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and manage network resources to meet diverse quality of service (QoS) requirements. We propose a mixed-integer nonlinear programming (MINLP) formulation for the considered NS problem that can flexibly route the traffic flow of the services on multiple paths and provide end-to-end delay and reliability guarantees for all services. To overcome the computational difficulty due to the intrinsic nonlinearity in the MINLP formulation, we transform the MINLP formulation into an equivalent mixed-integer linear programming (MILP) formulation and further show that their continuous relaxations are equivalent. In sharp contrast to the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial-time solvable linear programming problem, which significantly facilitates the algorithmic design. Based on the newly proposed MILP formulation, we develop a customized column generation (cCG) algorithm for solving the NS problem. The proposed cCG algorithm is a decomposition-based algorithm and is particularly suitable for solving large-scale NS problems. Numerical results demonstrate the efficacy of the proposed formulations and the proposed cCG algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge