QoS-Aware and Routing-Flexible Network Slicing for Service-Oriented Networks

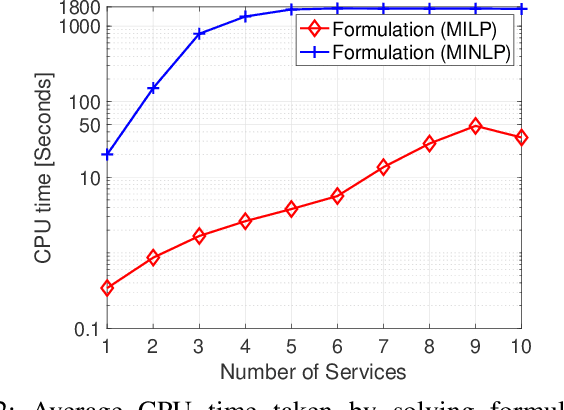
In this paper, we consider the network slicing (NS) problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and manage network resources to meet diverse quality of service (QoS) requirements. We propose a mixed-integer nonlinear programming (MINLP) formulation for the considered NS problem that can flexibly route the traffic flow of the services on multiple paths and provide end-to-end delay and reliability guarantees for all services. To overcome the computational difficulty due to the intrinsic nonlinearity in the MINLP formulation, we transform the MINLP formulation into an equivalent mixed-integer linear programming (MILP) formulation and further show that their continuous relaxations are equivalent. In sharp contrast to the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial-time solvable linear programming problem, which significantly facilitates the algorithmic design. Based on the newly proposed MILP formulation, we develop a customized column generation (cCG) algorithm for solving the NS problem. The proposed cCG algorithm is a decomposition-based algorithm and is particularly suitable for solving large-scale NS problems. Numerical results demonstrate the efficacy of the proposed formulations and the proposed cCG algorithm.

An Efficient Decomposition Algorithm for Large-Scale Network Slicing

In this paper, we consider the network slicing (NS) problem which attempts to map multiple customized virtual network requests to a common shared network infrastructure and allocate network resources to meet diverse service requirements. We propose an efficient decomposition algorithm for solving this NP-hard problem. The proposed algorithm decomposes the large-scale hard NS problem into two relatively easy function placement (FP) and traffic routing (TR) subproblems and iteratively solves them enabling information feedback between each other, which makes it particularly suitable to solve large-scale problems. Specifically, the FP subproblem is to place service functions into cloud nodes in the network, and solving it can return a function placement strategy based on which the TR subproblem is defined; and the TR subproblem is to find paths connecting two nodes hosting two adjacent functions in the network, and solving it can either verify that the solution of the FP subproblem is an optimal solution of the original problem, or return a valid inequality to the FP subproblem that cuts off the current infeasible solution. The proposed algorithm is guaranteed to find the global solution of the NS problem. We demonstrate the effectiveness and efficiency of the proposed algorithm via numerical experiments.

Primal Dual Alternating Proximal Gradient Algorithms for Nonsmooth Nonconvex Minimax Problems with Coupled Linear Constraints

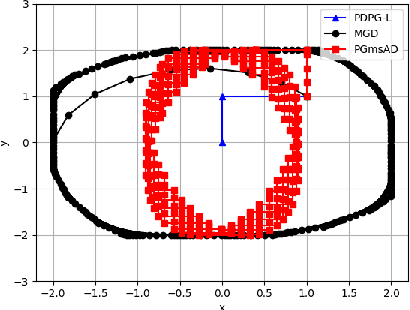
Nonconvex minimax problems have attracted wide attention in machine learning, signal processing and many other fields in recent years. In this paper, we propose a primal dual alternating proximal gradient (PDAPG) algorithm and a primal dual proximal gradient (PDPG-L) algorithm for solving nonsmooth nonconvex-strongly concave and nonconvex-linear minimax problems with coupled linear constraints, respectively. The corresponding iteration complexity of the two algorithms are proved to be $\mathcal{O}\left( \varepsilon ^{-2} \right)$ and $\mathcal{O}\left( \varepsilon ^{-3} \right)$ to reach an $\varepsilon$-stationary point, respectively. To our knowledge, they are the first two algorithms with iteration complexity guarantee for solving the two classes of minimax problems.

Zeroth-Order Alternating Gradient Descent Ascent Algorithms for a Class of Nonconvex-Nonconcave Minimax Problems

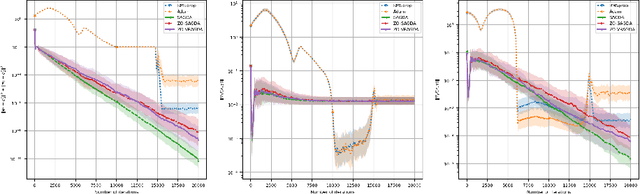
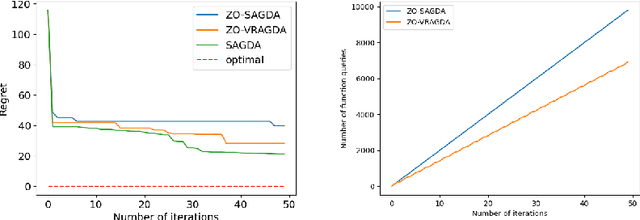
In this paper, we consider a class of nonconvex-nonconcave minimax problems, i.e., NC-PL minimax problems, whose objective functions satisfy the Polyak-$\L$ojasiewicz (PL) condition with respect to the inner variable. We propose a zeroth-order alternating gradient descent ascent (ZO-AGDA) algorithm and a zeroth-order variance reduced alternating gradient descent ascent (ZO-VRAGDA) algorithm for solving NC-PL minimax problem under the deterministic and the stochastic setting, respectively. The number of iterations to obtain an $\epsilon$-stationary point of ZO-AGDA and ZO-VRAGDA algorithm for solving NC-PL minimax problem is upper bounded by $\mathcal{O}(\varepsilon^{-2})$ and $\mathcal{O}(\varepsilon^{-3})$, respectively. To the best of our knowledge, they are the first two zeroth-order algorithms with the iteration complexity gurantee for solving NC-PL minimax problems.

Efficient Quantized Constant Envelope Precoding for Multiuser Downlink Massive MIMO Systems

Quantized constant envelope (QCE) precoding, a new transmission scheme that only discrete QCE transmit signals are allowed at each antenna, has gained growing research interests due to its ability of reducing the hardware cost and the energy consumption of massive multiple-input multiple-output (MIMO) systems. However, the discrete nature of QCE transmit signals greatly complicates the precoding design. In this paper, we consider the QCE precoding problem for a massive MIMO system with phase shift keying (PSK) modulation and develop an efficient approach for solving the constructive interference (CI) based problem formulation. Our approach is based on a custom-designed (continuous) penalty model that is equivalent to the original discrete problem. Specifically, the penalty model relaxes the discrete QCE constraint and penalizes it in the objective with a negative $\ell_2$-norm term, which leads to a non-smooth non-convex optimization problem. To tackle it, we resort to our recently proposed alternating optimization (AO) algorithm. We show that the AO algorithm admits closed-form updates at each iteration when applied to our problem and thus can be efficiently implemented. Simulation results demonstrate the superiority of the proposed approach over the existing algorithms.

CI-Based One-Bit Precoding for Multiuser Downlink Massive MIMO Systems with PSK Modulation: A Negative $\ell_1$ Penalty Approach

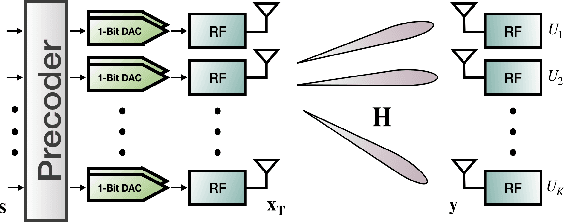
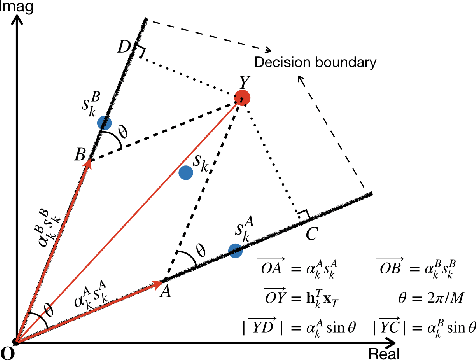
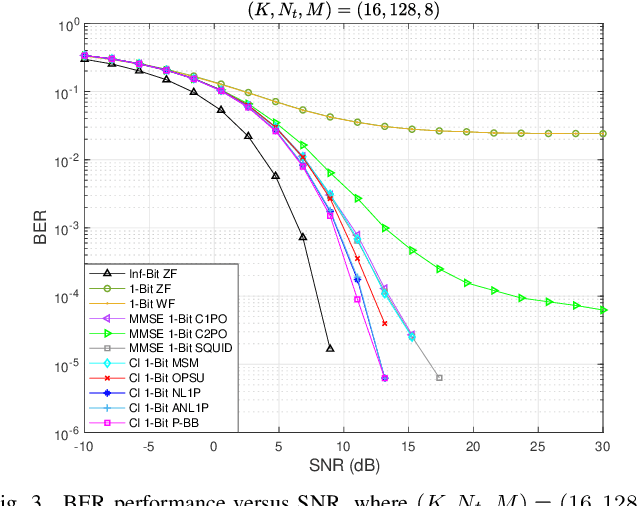
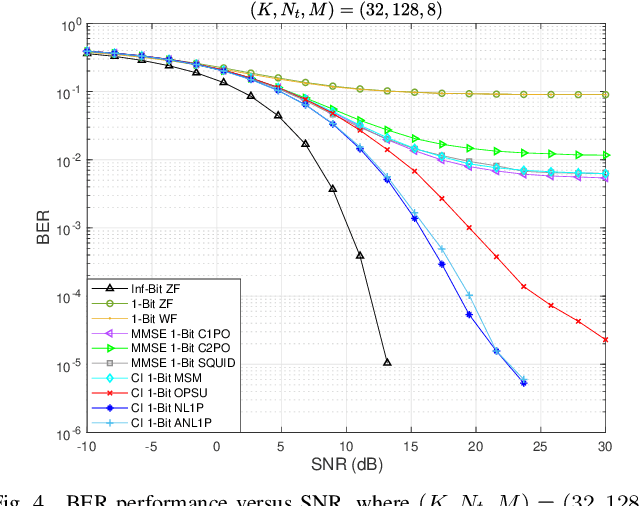
In this paper, we consider the one-bit precoding problem for the multiuser downlink massive multiple-input multiple-output (MIMO) system with phase shift keying (PSK) modulation and focus on the celebrated constructive interference (CI)-based problem formulation. We first establish the NP-hardness of the problem (even in the single-user case), which reveals the intrinsic difficulty of globally solving the problem. Then, we propose a novel negative $\ell_1$ penalty model for the considered problem, which penalizes the one-bit constraint into the objective with a negative $\ell_1$-norm term, and show the equivalence between (global and local) solutions of the original problem and the penalty problem when the penalty parameter is sufficiently large. We further transform the penalty model into an equivalent min-max problem and propose an efficient alternating optimization (AO) algorithm for solving it. The AO algorithm enjoys low per-iteration complexity and is guaranteed to converge to the stationary point of the min-max problem. To further reduce the computational cost, we also propose a low-complexity implementation of the AO algorithm, where the values of the variables will be fixed in later iterations once they satisfy the one-bit constraint. Numerical results show that, compared against the state-of-the-art CI-based algorithms, both of the proposed algorithms generally achieve better bit-error-rate (BER) performance with lower computational cost, especially when the problem is difficult (e.g., high-order modulations, large number of antennas, or high user-antenna ratio).

Optimal QoS-Aware Network Slicing for Service-Oriented Networks with Flexible Routing

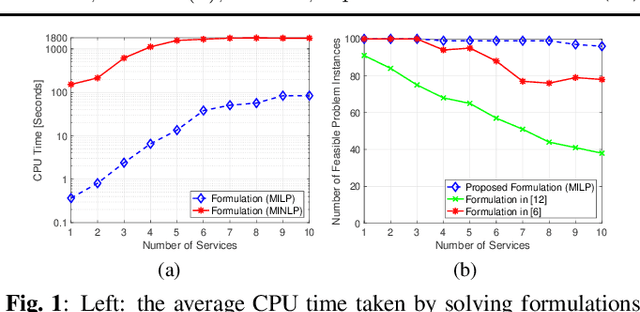
In this paper, we consider the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse quality of service (QoS) requirements. We first propose a mixed integer nonlinear program (MINLP) formulation for this problem that optimizes the network resource consumption while jointly considers QoS requirements, flow routing, and resource budget constraints. In particular, the proposed formulation is able to flexibly route the traffic flow of the services on multiple paths and provide end-to-end (E2E) delay and reliability guarantees for all services. Due to the intrinsic nonlinearity, the MINLP formulation is computationally difficult to solve. To overcome this difficulty, we then propose a mixed integer linear program (MILP) formulation and show that the two formulations and their continuous relaxations are equivalent. Different from the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial time solvable linear programming problem, which makes the MILP formulation much more computationally solvable. Numerical results demonstrate the effectiveness and efficiency of the proposed formulations over existing ones.

A Novel Negative $\ell_1$ Penalty Approach for Multiuser One-Bit Massive MIMO Downlink with PSK Signaling

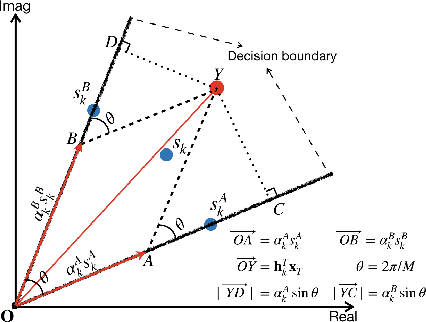
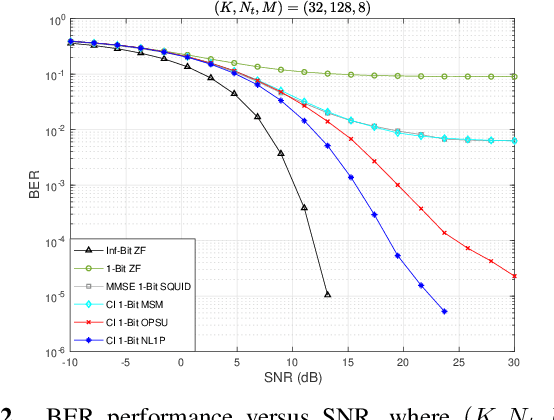
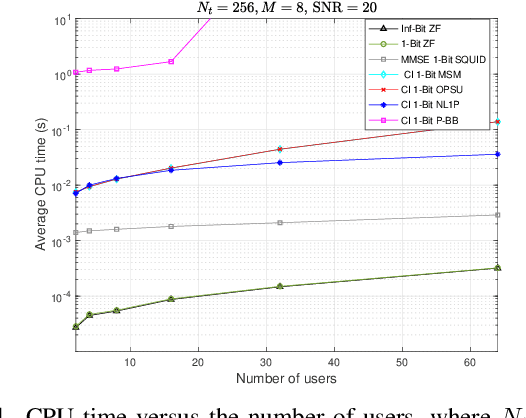
This paper considers the one-bit precoding problem for the multiuser downlink massive multiple-input multiple-output (MIMO) system with phase shift keying (PSK) modulation and focuses on the celebrated constructive interference (CI)-based problem formulation. The existence of the discrete one-bit constraint makes the problem generally hard to solve. In this paper, we propose an efficient negative $\ell_1$ penalty approach for finding a high-quality solution of the considered problem. Specifically, we first propose a novel negative $\ell_1$ penalty model, which penalizes the one-bit constraint into the objective with a negative $\ell_1$-norm term, and show the equivalence between (global and local) solutions of the original problem and the penalty problem when the penalty parameter is sufficiently large. We further transform the penalty model into an equivalent min-max problem and propose an efficient alternating optimization (AO) algorithm for solving it. The AO algorithm enjoys low per-iteration complexity and is guaranteed to converge to the stationary point of the min-max problem. Numerical results show that, compared against the state-of-the-art CI-based algorithms, the proposed algorithm generally achieves better bit-error-rate (BER) performance with lower computational cost.

Towards Efficient Large-Scale Network Slicing: An LP Rounding-and-Refinement Approach

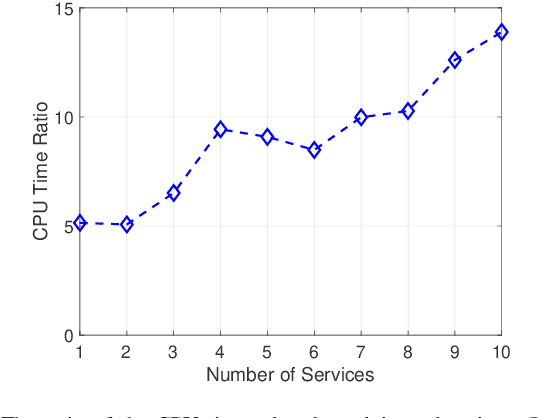
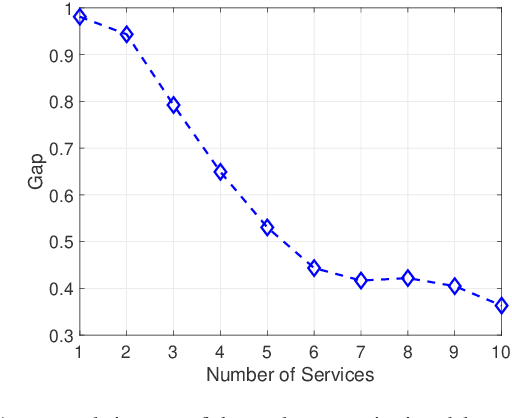
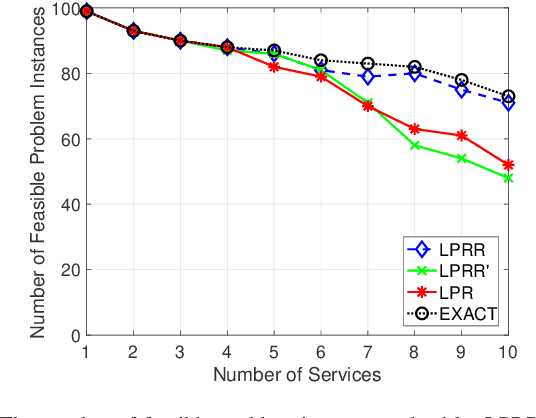
In this paper, we propose an efficient algorithm for the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse service requirements. The problem has been formulated as a mixed integer linear programming (MILP) formulation in the literature. By exploiting the special structure of the network slicing problem, we first propose a novel linear programming (LP) relaxation of the MILP formulation. We show that compared with a natural LP relaxation of the MILP formulation, the novel LP relaxation is much more compact in terms of smaller numbers of variables and constraints, and much stronger in terms of providing a better LP bound, which makes it particularly suitable to be embedded in an LP based algorithm. Then we design an efficient two-stage LP rounding-and-refinement algorithm based on this novel LP relaxation. In the first stage, the proposed algorithm uses an iterative LP rounding procedure to place the virtual network functions of all services into cloud nodes while taking traffic routing of all services into consideration; in the second stage, the proposed algorithm uses an iterative LP refinement procedure to obtain a solution for traffic routing of all services with their end-to-end delay constraints being satisfied. Compared with the existing algorithms which either have an exponential complexity or return a low-quality solution, our proposed algorithm achieves a better trade-off between the solution quality and the computational complexity. In particular, the worst-case complexity of our proposed algorithm is polynomial, which makes it suitable for solving large-scale problems. Numerical results demonstrate the effectiveness and efficiency of our proposed algorithm.

An efficient linear programming rounding-and-refinement algorithm for large-scale network slicing problem

In this paper, we consider the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse service requirements, and propose an efficient two-stage algorithm for solving this NP-hard problem. In the first stage, the proposed algorithm uses an iterative linear programming (LP) rounding procedure to place the virtual network functions of all services into cloud nodes while taking traffic routing of all services into consideration; in the second stage, the proposed algorithm uses an iterative LP refinement procedure to obtain a solution for traffic routing of all services with their end-to-end delay constraints being satisfied. Compared with the existing algorithms which either have an exponential complexity or return a low-quality solution, our proposed algorithm achieves a better trade-off between solution quality and computational complexity. In particular, the worst-case complexity of our proposed algorithm is polynomial, which makes it suitable for solving large-scale problems. Numerical results demonstrate the effectiveness and efficiency of our proposed algorithm.