Optimal QoS-Aware Network Slicing for Service-Oriented Networks with Flexible Routing
Paper and Code
Oct 12, 2021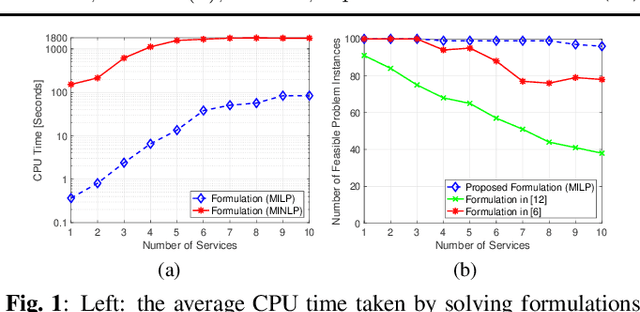
In this paper, we consider the network slicing problem which attempts to map multiple customized virtual network requests (also called services) to a common shared network infrastructure and allocate network resources to meet diverse quality of service (QoS) requirements. We first propose a mixed integer nonlinear program (MINLP) formulation for this problem that optimizes the network resource consumption while jointly considers QoS requirements, flow routing, and resource budget constraints. In particular, the proposed formulation is able to flexibly route the traffic flow of the services on multiple paths and provide end-to-end (E2E) delay and reliability guarantees for all services. Due to the intrinsic nonlinearity, the MINLP formulation is computationally difficult to solve. To overcome this difficulty, we then propose a mixed integer linear program (MILP) formulation and show that the two formulations and their continuous relaxations are equivalent. Different from the continuous relaxation of the MINLP formulation which is a nonconvex nonlinear programming problem, the continuous relaxation of the MILP formulation is a polynomial time solvable linear programming problem, which makes the MILP formulation much more computationally solvable. Numerical results demonstrate the effectiveness and efficiency of the proposed formulations over existing ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge