Gradient Norm Regularization Second-Order Algorithms for Solving Nonconvex-Strongly Concave Minimax Problems

In this paper, we study second-order algorithms for solving nonconvex-strongly concave minimax problems, which have attracted much attention in recent years in many fields, especially in machine learning. We propose a gradient norm regularized trust region (GRTR) algorithm to solve nonconvex-strongly concave minimax problems, where the objective function of the trust region subproblem in each iteration uses a regularized version of the Hessian matrix, and the regularization coefficient and the radius of the ball constraint are proportional to the square root of the gradient norm. The iteration complexity of the proposed GRTR algorithm to obtain an $\mathcal{O}(\epsilon,\sqrt{\epsilon})$-second-order stationary point is proved to be upper bounded by $\tilde{\mathcal{O}}(\rho^{0.5}\kappa^{1.5}\epsilon^{-3/2})$, where $\rho$ and $\kappa$ are the Lipschitz constant of the Jacobian matrix and the condition number of the objective function respectively, which matches the best known iteration complexity of second-order methods for solving nonconvex-strongly concave minimax problems. We further propose a Levenberg-Marquardt algorithm with a gradient norm regularization coefficient and use the negative curvature direction to correct the iteration direction (LMNegCur), which does not need to solve the trust region subproblem at each iteration. We also prove that the LMNegCur algorithm achieves an $\mathcal{O}(\epsilon,\sqrt{\epsilon})$-second-order stationary point within $\tilde{\mathcal{O}}(\rho^{0.5}\kappa^{1.5}\epsilon^{-3/2})$ number of iterations. Numerical results show the efficiency of both proposed algorithms.

Zeroth-Order Stochastic Mirror Descent Algorithms for Minimax Excess Risk Optimization

The minimax excess risk optimization (MERO) problem is a new variation of the traditional distributionally robust optimization (DRO) problem, which achieves uniformly low regret across all test distributions under suitable conditions. In this paper, we propose a zeroth-order stochastic mirror descent (ZO-SMD) algorithm available for both smooth and non-smooth MERO to estimate the minimal risk of each distrbution, and finally solve MERO as (non-)smooth stochastic convex-concave (linear) minimax optimization problems. The proposed algorithm is proved to converge at optimal convergence rates of $\mathcal{O}\left(1/\sqrt{t}\right)$ on the estimate of $R_i^*$ and $\mathcal{O}\left(1/\sqrt{t}\right)$ on the optimization error of both smooth and non-smooth MERO. Numerical results show the efficiency of the proposed algorithm.

Two Completely Parameter-Free Alternating Gradient Projection Algorithms for Nonconvex-(strongly) Concave Minimax Problems

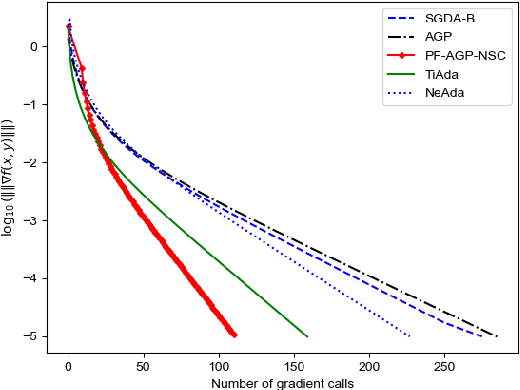
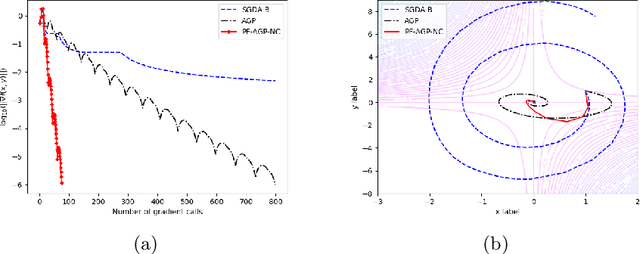
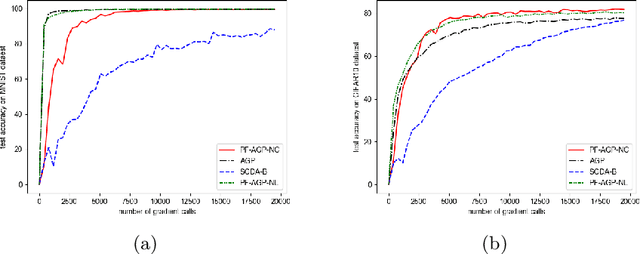
Due to their importance in various emerging applications, efficient algorithms for solving minimax problems have recently received increasing attention. However, many existing algorithms require prior knowledge of the problem parameters in order to achieve optimal iteration complexity. In this paper, we propose a completely parameter-free alternating gradient projection (PF-AGP) algorithm to solve the smooth nonconvex-(strongly) concave minimax problems using a backtracking strategy, which does not require prior knowledge of parameters such as the Lipschtiz constant $L$ or the strongly concave constant $\mu$. The PF-AGP algorithm utilizes a parameter-free gradient projection step to alternately update the outer and inner variables in each iteration. We show that the total number of gradient calls of the PF-AGP algorithm to obtain an $\varepsilon$-stationary point for nonconvex-strongly concave minimax problems is upper bounded by $\mathcal{O}\left( L\kappa^3\varepsilon^{-2} \right)$ where $\kappa$ is the condition number, while the total number of gradient calls to obtain an $\varepsilon$-stationary point for nonconvex-concave minimax problems is upper bounded by $\mathcal{O}\left( L^4\varepsilon^{-4} \right)$. As far as we know, this is the first completely parameter-free algorithm for solving nonconvex-strongly concave minimax problems, and it is also the completely parameter-free algorithm which achieves the best iteration complexity in single loop method for solving nonconvex-concave minimax problems. Numerical results validate the efficiency of the proposed PF-AGP algorithm.

A Fully Parameter-Free Second-Order Algorithm for Convex-Concave Minimax Problems with Optimal Iteration Complexity

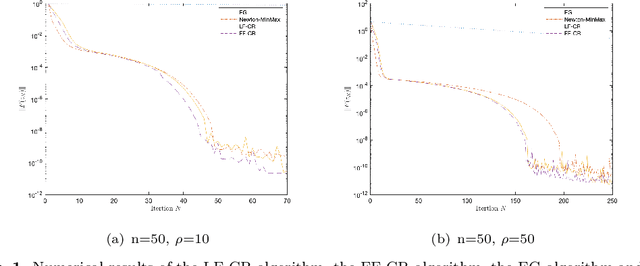
In this paper, we study second-order algorithms for the convex-concave minimax problem, which has attracted much attention in many fields such as machine learning in recent years. We propose a Lipschitz-free cubic regularization (LF-CR) algorithm for solving the convex-concave minimax optimization problem without knowing the Lipschitz constant. It can be shown that the iteration complexity of the LF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the restricted primal-dual gap is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^3}{\epsilon})^{\frac{2}{3}}$, where $z^0=(x^0,y^0)$ is a pair of initial points, $z^*=(x^*,y^*)$ is a pair of optimal solutions, and $\rho$ is the Lipschitz constant. We further propose a fully parameter-free cubic regularization (FF-CR) algorithm that does not require any parameters of the problem, including the Lipschitz constant and the upper bound of the distance from the initial point to the optimal solution. We also prove that the iteration complexity of the FF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the gradient norm is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^2}{\epsilon})^{\frac{2}{3}}$. Numerical experiments show the efficiency of both algorithms. To the best of our knowledge, the proposed FF-CR algorithm is the first completely parameter-free second-order algorithm for solving convex-concave minimax optimization problems, and its iteration complexity is consistent with the optimal iteration complexity lower bound of existing second-order algorithms with parameters for solving convex-concave minimax problems.

Two trust region type algorithms for solving nonconvex-strongly concave minimax problems

In this paper, we propose a Minimax Trust Region (MINIMAX-TR) algorithm and a Minimax Trust Region Algorithm with Contractions and Expansions(MINIMAX-TRACE) algorithm for solving nonconvex-strongly concave minimax problems. Both algorithms can find an $(\epsilon, \sqrt{\epsilon})$-second order stationary point(SSP) within $\mathcal{O}(\epsilon^{-1.5})$ iterations, which matches the best well known iteration complexity.

Zeroth-Order primal-dual Alternating Projection Gradient Algorithms for Nonconvex Minimax Problems with Coupled linear Constraints

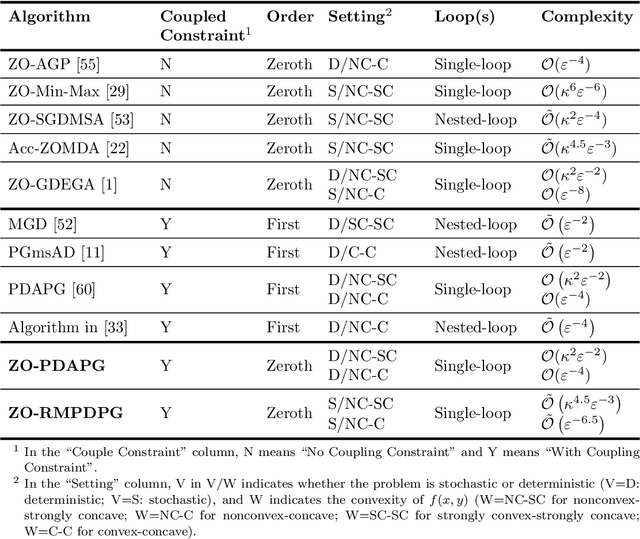
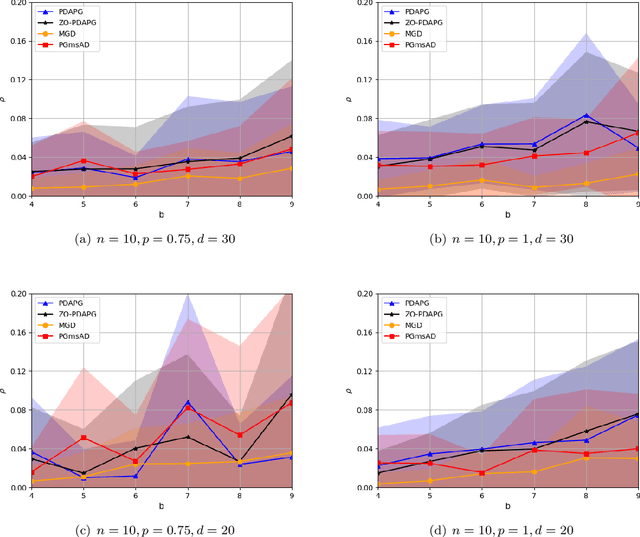
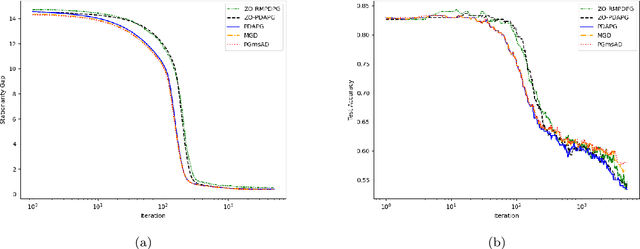
In this paper, we study zeroth-order algorithms for nonconvex minimax problems with coupled linear constraints under the deterministic and stochastic settings, which have attracted wide attention in machine learning, signal processing and many other fields in recent years, e.g., adversarial attacks in resource allocation problems and network flow problems etc. We propose two single-loop algorithms, namely the zero-order primal-dual alternating projected gradient (ZO-PDAPG) algorithm and the zero-order regularized momentum primal-dual projected gradient algorithm (ZO-RMPDPG), for solving deterministic and stochastic nonconvex-(strongly) concave minimax problems with coupled linear constraints. The iteration complexity of the two proposed algorithms to obtain an $\varepsilon$-stationary point are proved to be $\mathcal{O}(\varepsilon ^{-2})$ (resp. $\mathcal{O}(\varepsilon ^{-4})$) for solving nonconvex-strongly concave (resp. nonconvex-concave) minimax problems with coupled linear constraints under deterministic settings and $\tilde{\mathcal{O}}(\varepsilon ^{-3})$ (resp. $\tilde{\mathcal{O}}(\varepsilon ^{-6.5})$) under stochastic settings respectively. To the best of our knowledge, they are the first two zeroth-order algorithms with iterative complexity guarantees for solving nonconvex-(strongly) concave minimax problems with coupled linear constraints under the deterministic and stochastic settings.

An accelerated first-order regularized momentum descent ascent algorithm for stochastic nonconvex-concave minimax problems

Stochastic nonconvex minimax problems have attracted wide attention in machine learning, signal processing and many other fields in recent years. In this paper, we propose an accelerated first-order regularized momentum descent ascent algorithm (FORMDA) for solving stochastic nonconvex-concave minimax problems. The iteration complexity of the algorithm is proved to be $\tilde{\mathcal{O}}(\varepsilon ^{-6.5})$ to obtain an $\varepsilon$-stationary point, which achieves the best-known complexity bound for single-loop algorithms to solve the stochastic nonconvex-concave minimax problems under the stationarity of the objective function.

Primal Dual Alternating Proximal Gradient Algorithms for Nonsmooth Nonconvex Minimax Problems with Coupled Linear Constraints

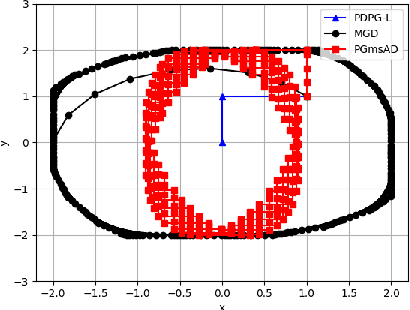
Nonconvex minimax problems have attracted wide attention in machine learning, signal processing and many other fields in recent years. In this paper, we propose a primal dual alternating proximal gradient (PDAPG) algorithm and a primal dual proximal gradient (PDPG-L) algorithm for solving nonsmooth nonconvex-strongly concave and nonconvex-linear minimax problems with coupled linear constraints, respectively. The corresponding iteration complexity of the two algorithms are proved to be $\mathcal{O}\left( \varepsilon ^{-2} \right)$ and $\mathcal{O}\left( \varepsilon ^{-3} \right)$ to reach an $\varepsilon$-stationary point, respectively. To our knowledge, they are the first two algorithms with iteration complexity guarantee for solving the two classes of minimax problems.

Zeroth-Order Alternating Gradient Descent Ascent Algorithms for a Class of Nonconvex-Nonconcave Minimax Problems

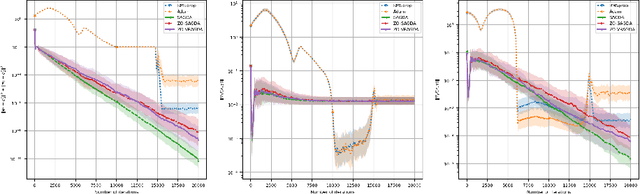
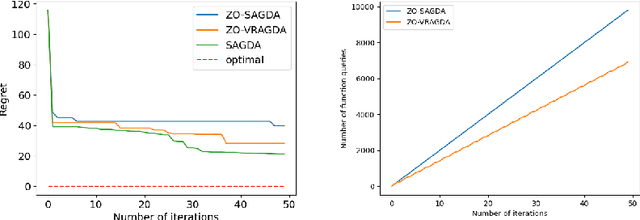
In this paper, we consider a class of nonconvex-nonconcave minimax problems, i.e., NC-PL minimax problems, whose objective functions satisfy the Polyak-$\L$ojasiewicz (PL) condition with respect to the inner variable. We propose a zeroth-order alternating gradient descent ascent (ZO-AGDA) algorithm and a zeroth-order variance reduced alternating gradient descent ascent (ZO-VRAGDA) algorithm for solving NC-PL minimax problem under the deterministic and the stochastic setting, respectively. The number of iterations to obtain an $\epsilon$-stationary point of ZO-AGDA and ZO-VRAGDA algorithm for solving NC-PL minimax problem is upper bounded by $\mathcal{O}(\varepsilon^{-2})$ and $\mathcal{O}(\varepsilon^{-3})$, respectively. To the best of our knowledge, they are the first two zeroth-order algorithms with the iteration complexity gurantee for solving NC-PL minimax problems.

Zeroth-Order Alternating Randomized Gradient Projection Algorithms for General Nonconvex-Concave Minimax Problems

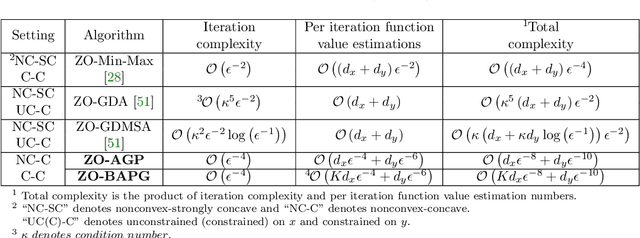
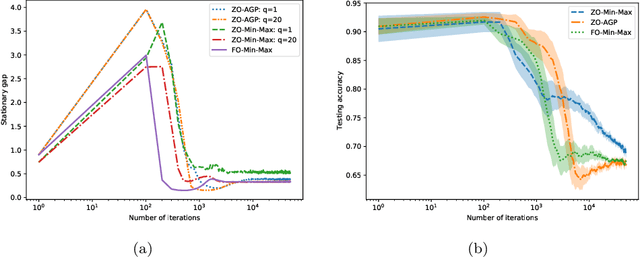
In this paper, we study zeroth-order algorithms for nonconvex-concave minimax problems, which have attracted widely attention in machine learning, signal processing and many other fields in recent years. We propose a zeroth-order alternating randomized gradient projection (ZO-AGP) algorithm for smooth nonconvex-concave minimax problems, and its iteration complexity to obtain an $\varepsilon$-stationary point is bounded by $\mathcal{O}(\varepsilon^{-4})$, and the number of function value estimation is bounded by $\mathcal{O}(d_{x}\varepsilon^{-4}+d_{y}\varepsilon^{-6})$ per iteration. Moreover, we propose a zeroth-order block alternating randomized proximal gradient algorithm (ZO-BAPG) for solving block-wise nonsmooth nonconvex-concave minimax optimization problems, and the iteration complexity to obtain an $\varepsilon$-stationary point is bounded by $\mathcal{O}(\varepsilon^{-4})$ and the number of function value estimation per iteration is bounded by $\mathcal{O}(K d_{x}\varepsilon^{-4}+d_{y}\varepsilon^{-6})$. To the best of our knowledge, this is the first time that zeroth-order algorithms with iteration complexity gurantee are developed for solving both general smooth and block-wise nonsmooth nonconvex-concave minimax problems. Numerical results on data poisoning attack problem validate the efficiency of the proposed algorithms.