Zeroth-Order primal-dual Alternating Projection Gradient Algorithms for Nonconvex Minimax Problems with Coupled linear Constraints
Paper and Code
Jan 26, 2024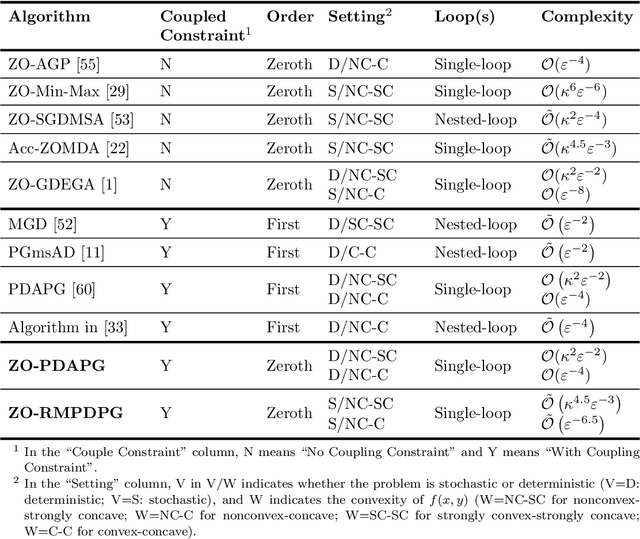
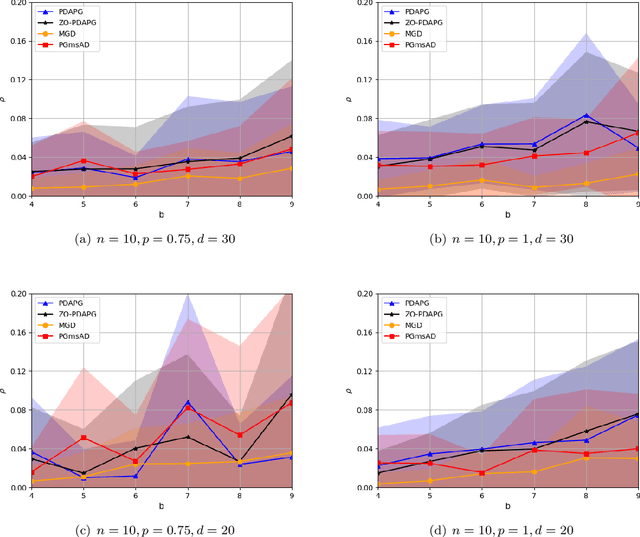
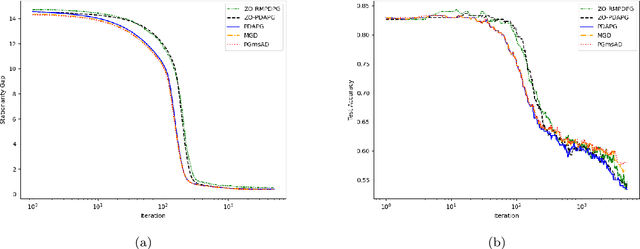
In this paper, we study zeroth-order algorithms for nonconvex minimax problems with coupled linear constraints under the deterministic and stochastic settings, which have attracted wide attention in machine learning, signal processing and many other fields in recent years, e.g., adversarial attacks in resource allocation problems and network flow problems etc. We propose two single-loop algorithms, namely the zero-order primal-dual alternating projected gradient (ZO-PDAPG) algorithm and the zero-order regularized momentum primal-dual projected gradient algorithm (ZO-RMPDPG), for solving deterministic and stochastic nonconvex-(strongly) concave minimax problems with coupled linear constraints. The iteration complexity of the two proposed algorithms to obtain an $\varepsilon$-stationary point are proved to be $\mathcal{O}(\varepsilon ^{-2})$ (resp. $\mathcal{O}(\varepsilon ^{-4})$) for solving nonconvex-strongly concave (resp. nonconvex-concave) minimax problems with coupled linear constraints under deterministic settings and $\tilde{\mathcal{O}}(\varepsilon ^{-3})$ (resp. $\tilde{\mathcal{O}}(\varepsilon ^{-6.5})$) under stochastic settings respectively. To the best of our knowledge, they are the first two zeroth-order algorithms with iterative complexity guarantees for solving nonconvex-(strongly) concave minimax problems with coupled linear constraints under the deterministic and stochastic settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge