Zeroth-Order primal-dual Alternating Projection Gradient Algorithms for Nonconvex Minimax Problems with Coupled linear Constraints

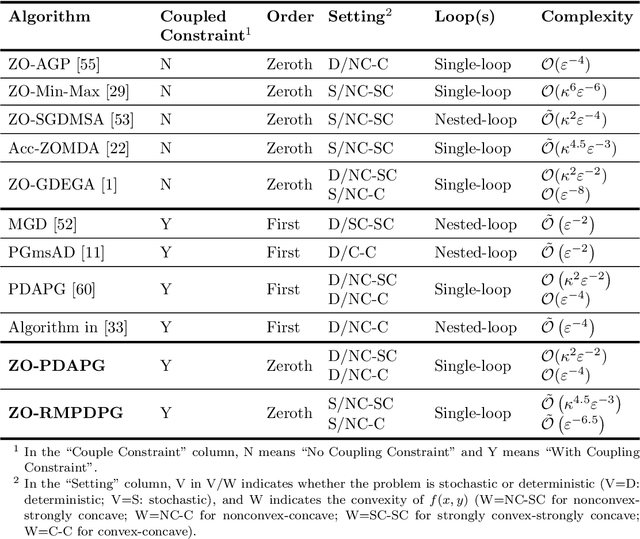
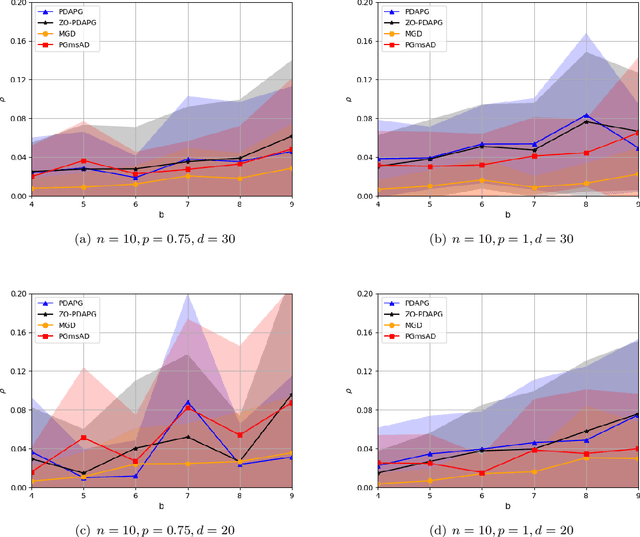
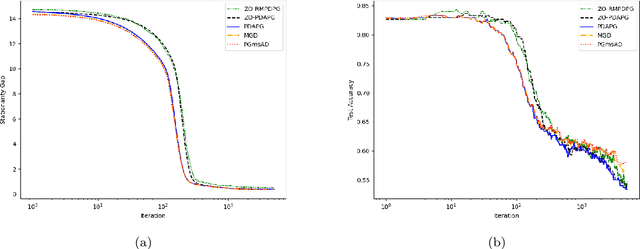
In this paper, we study zeroth-order algorithms for nonconvex minimax problems with coupled linear constraints under the deterministic and stochastic settings, which have attracted wide attention in machine learning, signal processing and many other fields in recent years, e.g., adversarial attacks in resource allocation problems and network flow problems etc. We propose two single-loop algorithms, namely the zero-order primal-dual alternating projected gradient (ZO-PDAPG) algorithm and the zero-order regularized momentum primal-dual projected gradient algorithm (ZO-RMPDPG), for solving deterministic and stochastic nonconvex-(strongly) concave minimax problems with coupled linear constraints. The iteration complexity of the two proposed algorithms to obtain an $\varepsilon$-stationary point are proved to be $\mathcal{O}(\varepsilon ^{-2})$ (resp. $\mathcal{O}(\varepsilon ^{-4})$) for solving nonconvex-strongly concave (resp. nonconvex-concave) minimax problems with coupled linear constraints under deterministic settings and $\tilde{\mathcal{O}}(\varepsilon ^{-3})$ (resp. $\tilde{\mathcal{O}}(\varepsilon ^{-6.5})$) under stochastic settings respectively. To the best of our knowledge, they are the first two zeroth-order algorithms with iterative complexity guarantees for solving nonconvex-(strongly) concave minimax problems with coupled linear constraints under the deterministic and stochastic settings.

Zeroth-Order Alternating Randomized Gradient Projection Algorithms for General Nonconvex-Concave Minimax Problems

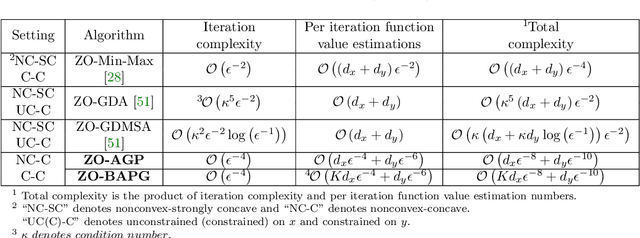
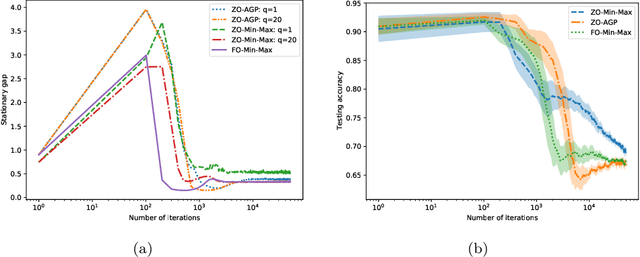
In this paper, we study zeroth-order algorithms for nonconvex-concave minimax problems, which have attracted widely attention in machine learning, signal processing and many other fields in recent years. We propose a zeroth-order alternating randomized gradient projection (ZO-AGP) algorithm for smooth nonconvex-concave minimax problems, and its iteration complexity to obtain an $\varepsilon$-stationary point is bounded by $\mathcal{O}(\varepsilon^{-4})$, and the number of function value estimation is bounded by $\mathcal{O}(d_{x}\varepsilon^{-4}+d_{y}\varepsilon^{-6})$ per iteration. Moreover, we propose a zeroth-order block alternating randomized proximal gradient algorithm (ZO-BAPG) for solving block-wise nonsmooth nonconvex-concave minimax optimization problems, and the iteration complexity to obtain an $\varepsilon$-stationary point is bounded by $\mathcal{O}(\varepsilon^{-4})$ and the number of function value estimation per iteration is bounded by $\mathcal{O}(K d_{x}\varepsilon^{-4}+d_{y}\varepsilon^{-6})$. To the best of our knowledge, this is the first time that zeroth-order algorithms with iteration complexity gurantee are developed for solving both general smooth and block-wise nonsmooth nonconvex-concave minimax problems. Numerical results on data poisoning attack problem validate the efficiency of the proposed algorithms.

Training GANs with Centripetal Acceleration

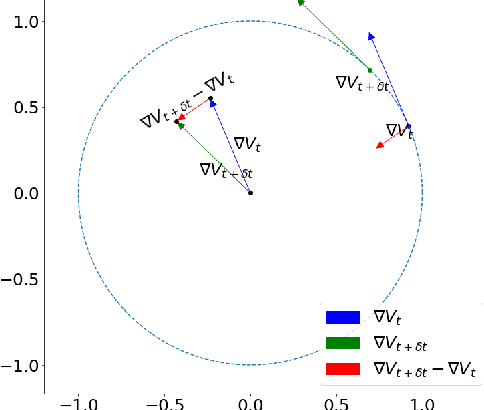
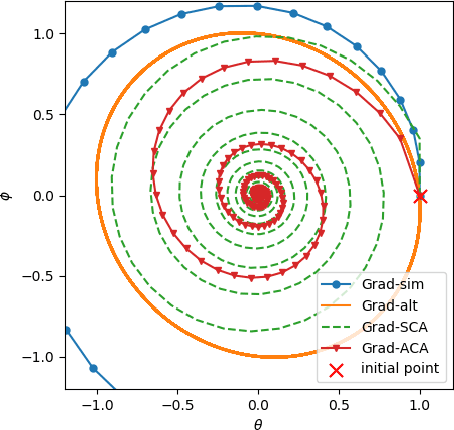
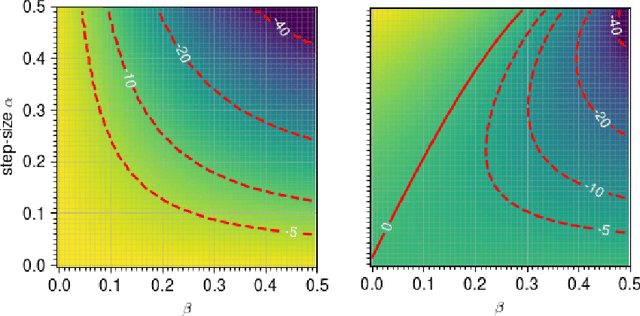
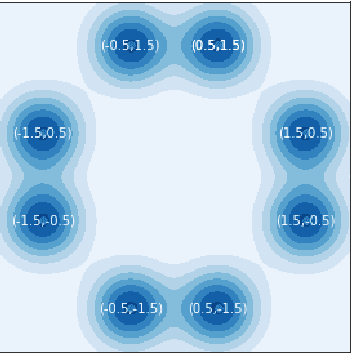
Training generative adversarial networks (GANs) often suffers from cyclic behaviors of iterates. Based on a simple intuition that the direction of centripetal acceleration of an object moving in uniform circular motion is toward the center of the circle, we present the Simultaneous Centripetal Acceleration (SCA) method and the Alternating Centripetal Acceleration (ACA) method to alleviate the cyclic behaviors. Under suitable conditions, gradient descent methods with either SCA or ACA are shown to be linearly convergent for bilinear games. Numerical experiments are conducted by applying ACA to existing gradient-based algorithms in a GAN setup scenario, which demonstrate the superiority of ACA.