A Fully Parameter-Free Second-Order Algorithm for Convex-Concave Minimax Problems with Optimal Iteration Complexity
Paper and Code
Jul 04, 2024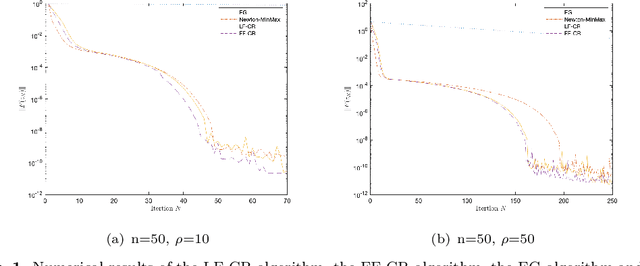
In this paper, we study second-order algorithms for the convex-concave minimax problem, which has attracted much attention in many fields such as machine learning in recent years. We propose a Lipschitz-free cubic regularization (LF-CR) algorithm for solving the convex-concave minimax optimization problem without knowing the Lipschitz constant. It can be shown that the iteration complexity of the LF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the restricted primal-dual gap is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^3}{\epsilon})^{\frac{2}{3}}$, where $z^0=(x^0,y^0)$ is a pair of initial points, $z^*=(x^*,y^*)$ is a pair of optimal solutions, and $\rho$ is the Lipschitz constant. We further propose a fully parameter-free cubic regularization (FF-CR) algorithm that does not require any parameters of the problem, including the Lipschitz constant and the upper bound of the distance from the initial point to the optimal solution. We also prove that the iteration complexity of the FF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the gradient norm is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^2}{\epsilon})^{\frac{2}{3}}$. Numerical experiments show the efficiency of both algorithms. To the best of our knowledge, the proposed FF-CR algorithm is the first completely parameter-free second-order algorithm for solving convex-concave minimax optimization problems, and its iteration complexity is consistent with the optimal iteration complexity lower bound of existing second-order algorithms with parameters for solving convex-concave minimax problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge