How Much Backtracking is Enough? Exploring the Interplay of SFT and RL in Enhancing LLM Reasoning

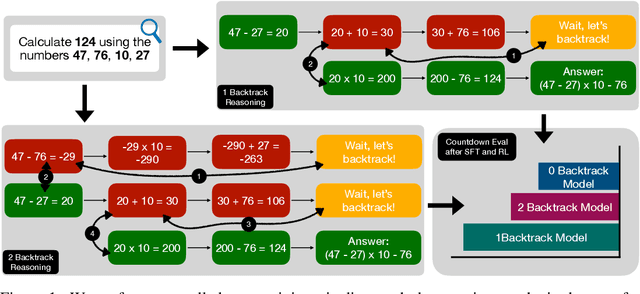
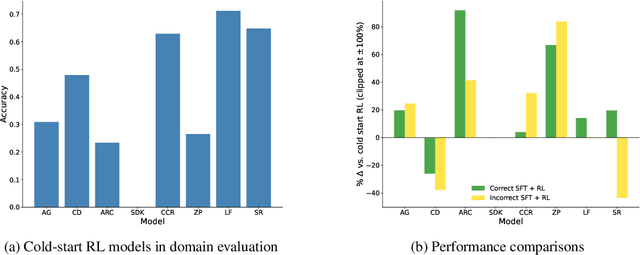
Recent breakthroughs in large language models (LLMs) have effectively improved their reasoning abilities, particularly on mathematical and logical problems that have verifiable answers, through techniques such as supervised finetuning (SFT) and reinforcement learning (RL). Prior research indicates that RL effectively internalizes search strategies, enabling long chain-of-thought (CoT) reasoning, with backtracking emerging naturally as a learned capability. However, the precise benefits of backtracking, specifically, how significantly it contributes to reasoning improvements and the optimal extent of its use, remain poorly understood. In this work, we systematically investigate the dynamics between SFT and RL on eight reasoning tasks: Countdown, Sudoku, Arc 1D, Geometry, Color Cube Rotation, List Functions, Zebra Puzzles, and Self Reference. Our findings highlight that short CoT sequences used in SFT as a warm-up do have moderate contribution to RL training, compared with cold-start RL; however such contribution diminishes when tasks become increasingly difficult. Motivated by this observation, we construct synthetic datasets varying systematically in the number of backtracking steps and conduct controlled experiments to isolate the influence of either the correctness (content) or the structure (i.e., backtrack frequency). We find that (1) longer CoT with backtracks generally induce better and more stable RL training, (2) more challenging problems with larger search space tend to need higher numbers of backtracks during the SFT stage. Additionally, we demonstrate through experiments on distilled data that RL training is largely unaffected by the correctness of long CoT sequences, suggesting that RL prioritizes structural patterns over content correctness. Collectively, our results offer practical insights into designing optimal training strategies to effectively scale reasoning in LLMs.

Grounding Bodily Awareness in Visual Representations for Efficient Policy Learning

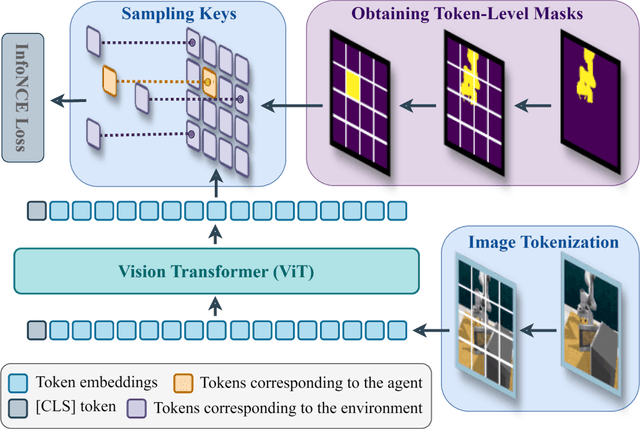
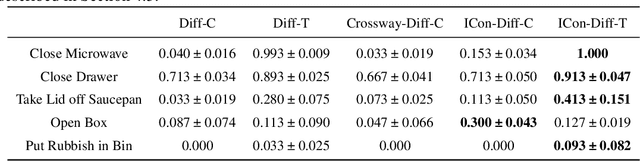
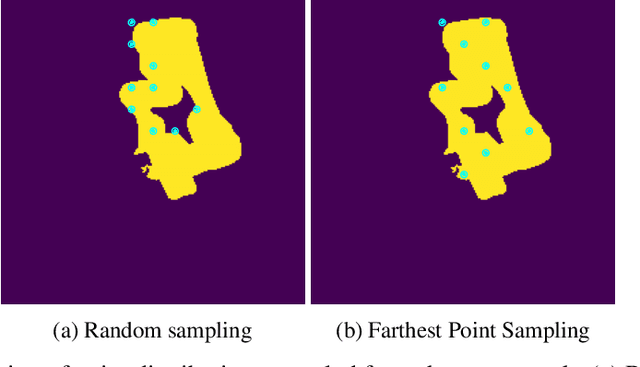
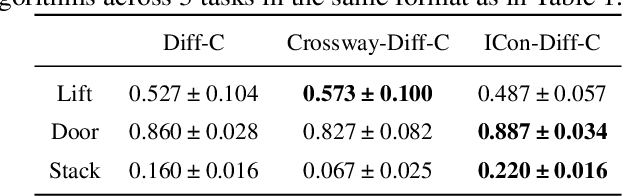
Learning effective visual representations for robotic manipulation remains a fundamental challenge due to the complex body dynamics involved in action execution. In this paper, we study how visual representations that carry body-relevant cues can enable efficient policy learning for downstream robotic manipulation tasks. We present $\textbf{I}$nter-token $\textbf{Con}$trast ($\textbf{ICon}$), a contrastive learning method applied to the token-level representations of Vision Transformers (ViTs). ICon enforces a separation in the feature space between agent-specific and environment-specific tokens, resulting in agent-centric visual representations that embed body-specific inductive biases. This framework can be seamlessly integrated into end-to-end policy learning by incorporating the contrastive loss as an auxiliary objective. Our experiments show that ICon not only improves policy performance across various manipulation tasks but also facilitates policy transfer across different robots. The project website: https://github.com/HenryWJL/icon

Atomic Consistency Preference Optimization for Long-Form Question Answering

Large Language Models (LLMs) frequently produce factoid hallucinations - plausible yet incorrect answers. A common mitigation strategy is model alignment, which improves factual accuracy by training on curated factual and non-factual pairs. However, this approach often relies on a stronger model (e.g., GPT-4) or an external knowledge base to assess factual correctness, which may not always be accessible. To address this, we propose Atomic Consistency Preference Optimization (ACPO), a self-supervised preference-tuning method that enhances factual accuracy without external supervision. ACPO leverages atomic consistency signals, i.e., the agreement of individual facts across multiple stochastic responses, to identify high- and low-quality data pairs for model alignment. By eliminating the need for costly GPT calls, ACPO provides a scalable and efficient approach to improving factoid question-answering. Despite being self-supervised, empirical results demonstrate that ACPO outperforms FactAlign, a strong supervised alignment baseline, by 1.95 points on the LongFact and BioGen datasets, highlighting its effectiveness in enhancing factual reliability without relying on external models or knowledge bases.

Improving Model Alignment Through Collective Intelligence of Open-Source LLMS

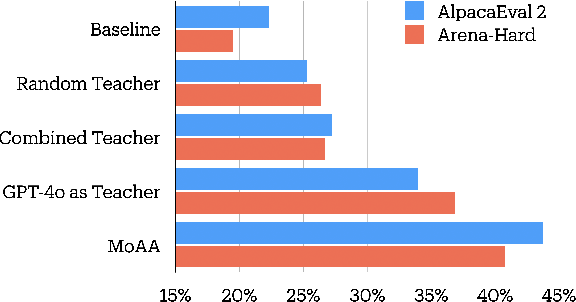
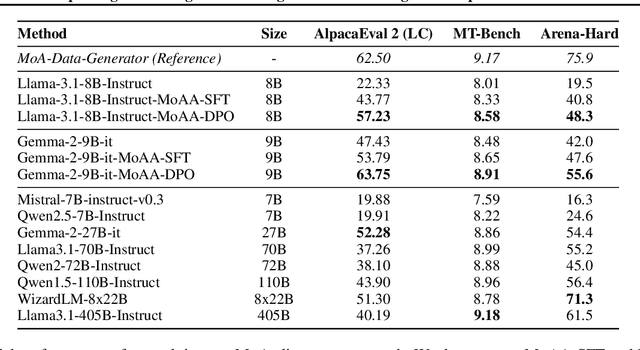
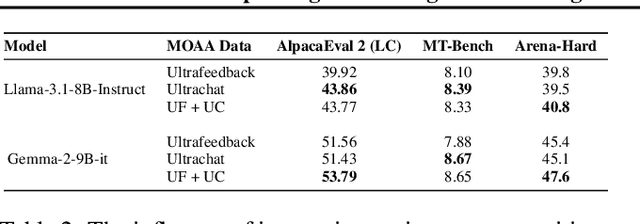
Building helpful and harmless large language models (LLMs) requires effective model alignment approach based on human instructions and feedback, which necessitates high-quality human-labeled data. Constructing such datasets is often expensive and hard to scale, and may face potential limitations on diversity and generalization. To address these challenges, we introduce Mixture of Agents Alignment (MoAA), that leverages the collective strengths of various language models to provide high-quality data for model alignment. By employing MoAA, we enhance both supervised fine-tuning and preference optimization, leading to improved performance compared to using a single model alone to generate alignment data (e.g. using GPT-4o alone). Evaluation results show that our approach can improve win rate of LLaMA-3.1-8B-Instruct from 19.5 to 48.3 on Arena-Hard and from 22.33 to 57.23 on AlpacaEval2, highlighting a promising direction for model alignment through this new scalable and diverse synthetic data recipe. Furthermore, we demonstrate that MoAA enables a self-improvement pipeline, where models finetuned on MoA-generated data surpass their own initial capabilities, providing evidence that our approach can push the frontier of open-source LLMs without reliance on stronger external supervision. Data and code will be released.

Think Deep, Think Fast: Investigating Efficiency of Verifier-free Inference-time-scaling Methods

There is intense interest in investigating how inference time compute (ITC) (e.g. repeated sampling, refinements, etc) can improve large language model (LLM) capabilities. At the same time, recent breakthroughs in reasoning models, such as Deepseek-R1, unlock the opportunity for reinforcement learning to improve LLM reasoning skills. An in-depth understanding of how ITC interacts with reasoning across different models could provide important guidance on how to further advance the LLM frontier. This work conducts a comprehensive analysis of inference-time scaling methods for both reasoning and non-reasoning models on challenging reasoning tasks. Specifically, we focus our research on verifier-free inference time-scaling methods due to its generalizability without needing a reward model. We construct the Pareto frontier of quality and efficiency. We find that non-reasoning models, even with an extremely high inference budget, still fall substantially behind reasoning models. For reasoning models, majority voting proves to be a robust inference strategy, generally competitive or outperforming other more sophisticated ITC methods like best-of-N and sequential revisions, while the additional inference compute offers minimal improvements. We further perform in-depth analyses of the association of key response features (length and linguistic markers) with response quality, with which we can improve the existing ITC methods. We find that correct responses from reasoning models are typically shorter and have fewer hedging and thinking markers (but more discourse markers) than the incorrect responses.

Knowing When to Stop: Dynamic Context Cutoff for Large Language Models

Large language models (LLMs) process entire input contexts indiscriminately, which is inefficient in cases where the information required to answer a query is localized within the context. We present dynamic context cutoff, a human-inspired method enabling LLMs to self-terminate processing upon acquiring sufficient task-relevant information. Through analysis of model internals, we discover that specific attention heads inherently encode "sufficiency signals" - detectable through lightweight classifiers - that predict when critical information has been processed. This reveals a new efficiency paradigm: models' internal understanding naturally dictates processing needs rather than external compression heuristics. Comprehensive experiments across six QA datasets (up to 40K tokens) with three model families (LLaMA/Qwen/Mistral, 1B0-70B) demonstrate 1.33x average token reduction while improving accuracy by 1.3%. Furthermore, our method demonstrates better performance with the same rate of token reduction compared to other context efficiency methods. Additionally, we observe an emergent scaling phenomenon: while smaller models require require probing for sufficiency detection, larger models exhibit intrinsic self-assessment capabilities through prompting.

A Fully Parameter-Free Second-Order Algorithm for Convex-Concave Minimax Problems with Optimal Iteration Complexity

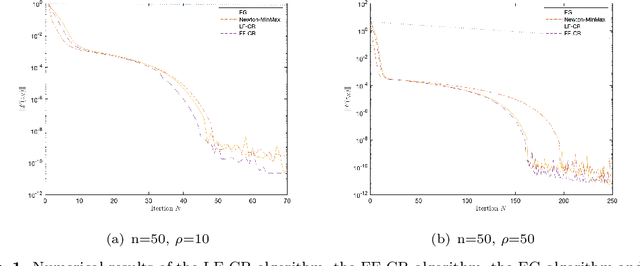
In this paper, we study second-order algorithms for the convex-concave minimax problem, which has attracted much attention in many fields such as machine learning in recent years. We propose a Lipschitz-free cubic regularization (LF-CR) algorithm for solving the convex-concave minimax optimization problem without knowing the Lipschitz constant. It can be shown that the iteration complexity of the LF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the restricted primal-dual gap is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^3}{\epsilon})^{\frac{2}{3}}$, where $z^0=(x^0,y^0)$ is a pair of initial points, $z^*=(x^*,y^*)$ is a pair of optimal solutions, and $\rho$ is the Lipschitz constant. We further propose a fully parameter-free cubic regularization (FF-CR) algorithm that does not require any parameters of the problem, including the Lipschitz constant and the upper bound of the distance from the initial point to the optimal solution. We also prove that the iteration complexity of the FF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the gradient norm is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^2}{\epsilon})^{\frac{2}{3}}$. Numerical experiments show the efficiency of both algorithms. To the best of our knowledge, the proposed FF-CR algorithm is the first completely parameter-free second-order algorithm for solving convex-concave minimax optimization problems, and its iteration complexity is consistent with the optimal iteration complexity lower bound of existing second-order algorithms with parameters for solving convex-concave minimax problems.

ReCaLL: Membership Inference via Relative Conditional Log-Likelihoods

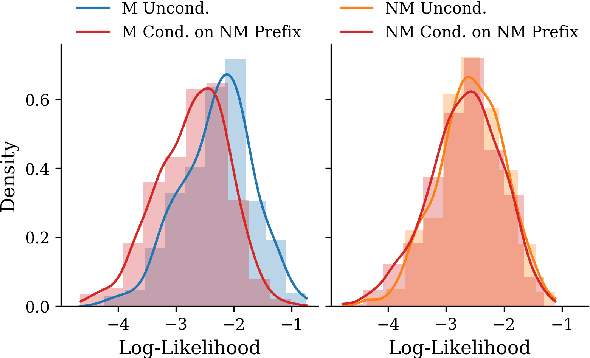
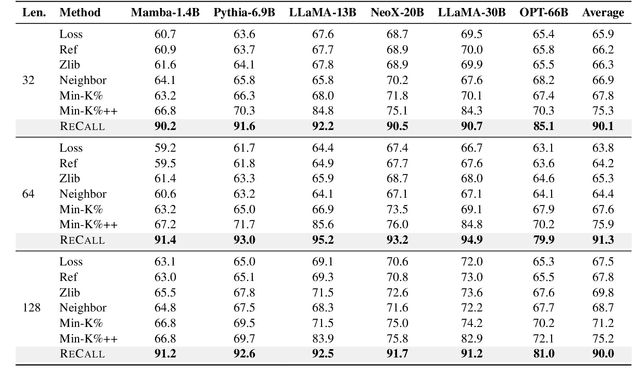
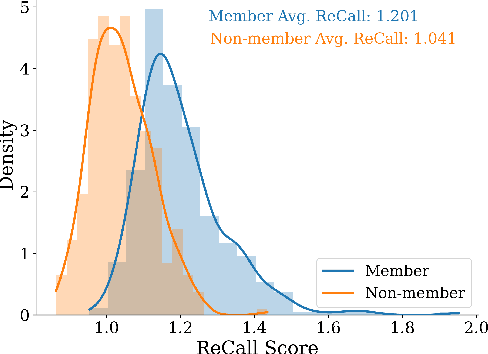
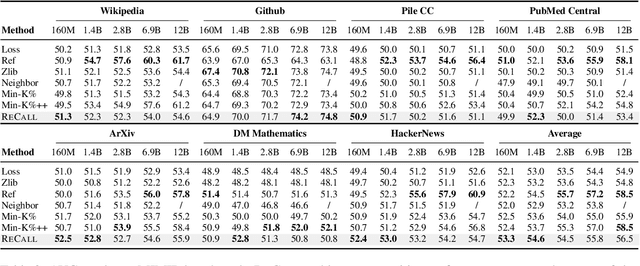
The rapid scaling of large language models (LLMs) has raised concerns about the transparency and fair use of the pretraining data used for training them. Detecting such content is challenging due to the scale of the data and limited exposure of each instance during training. We propose ReCaLL (Relative Conditional Log-Likelihood), a novel membership inference attack (MIA) to detect LLMs' pretraining data by leveraging their conditional language modeling capabilities. ReCaLL examines the relative change in conditional log-likelihoods when prefixing target data points with non-member context. Our empirical findings show that conditioning member data on non-member prefixes induces a larger decrease in log-likelihood compared to non-member data. We conduct comprehensive experiments and show that ReCaLL achieves state-of-the-art performance on the WikiMIA dataset, even with random and synthetic prefixes, and can be further improved using an ensemble approach. Moreover, we conduct an in-depth analysis of LLMs' behavior with different membership contexts, providing insights into how LLMs leverage membership information for effective inference at both the sequence and token level.

Reasoning in Token Economies: Budget-Aware Evaluation of LLM Reasoning Strategies

A diverse array of reasoning strategies has been proposed to elicit the capabilities of large language models. However, in this paper, we point out that traditional evaluations which focus solely on performance metrics miss a key factor: the increased effectiveness due to additional compute. By overlooking this aspect, a skewed view of strategy efficiency is often presented. This paper introduces a framework that incorporates the compute budget into the evaluation, providing a more informative comparison that takes into account both performance metrics and computational cost. In this budget-aware perspective, we find that complex reasoning strategies often don't surpass simpler baselines purely due to algorithmic ingenuity, but rather due to the larger computational resources allocated. When we provide a simple baseline like chain-of-thought self-consistency with comparable compute resources, it frequently outperforms reasoning strategies proposed in the literature. In this scale-aware perspective, we find that unlike self-consistency, certain strategies such as multi-agent debate or Reflexion can become worse if more compute budget is utilized.

Raccoon: Prompt Extraction Benchmark of LLM-Integrated Applications

With the proliferation of LLM-integrated applications such as GPT-s, millions are deployed, offering valuable services through proprietary instruction prompts. These systems, however, are prone to prompt extraction attacks through meticulously designed queries. To help mitigate this problem, we introduce the Raccoon benchmark which comprehensively evaluates a model's susceptibility to prompt extraction attacks. Our novel evaluation method assesses models under both defenseless and defended scenarios, employing a dual approach to evaluate the effectiveness of existing defenses and the resilience of the models. The benchmark encompasses 14 categories of prompt extraction attacks, with additional compounded attacks that closely mimic the strategies of potential attackers, alongside a diverse collection of defense templates. This array is, to our knowledge, the most extensive compilation of prompt theft attacks and defense mechanisms to date. Our findings highlight universal susceptibility to prompt theft in the absence of defenses, with OpenAI models demonstrating notable resilience when protected. This paper aims to establish a more systematic benchmark for assessing LLM robustness against prompt extraction attacks, offering insights into their causes and potential countermeasures. Resources of Raccoon are publicly available at https://github.com/M0gician/RaccoonBench.