Ruomin Huang
An Effective Dynamic Gradient Calibration Method for Continual Learning
Jul 30, 2024Abstract:Continual learning (CL) is a fundamental topic in machine learning, where the goal is to train a model with continuously incoming data and tasks. Due to the memory limit, we cannot store all the historical data, and therefore confront the ``catastrophic forgetting'' problem, i.e., the performance on the previous tasks can substantially decrease because of the missing information in the latter period. Though a number of elegant methods have been proposed, the catastrophic forgetting phenomenon still cannot be well avoided in practice. In this paper, we study the problem from the gradient perspective, where our aim is to develop an effective algorithm to calibrate the gradient in each updating step of the model; namely, our goal is to guide the model to be updated in the right direction under the situation that a large amount of historical data are unavailable. Our idea is partly inspired by the seminal stochastic variance reduction methods (e.g., SVRG and SAGA) for reducing the variance of gradient estimation in stochastic gradient descent algorithms. Another benefit is that our approach can be used as a general tool, which is able to be incorporated with several existing popular CL methods to achieve better performance. We also conduct a set of experiments on several benchmark datasets to evaluate the performance in practice.
ReCaLL: Membership Inference via Relative Conditional Log-Likelihoods
Jun 23, 2024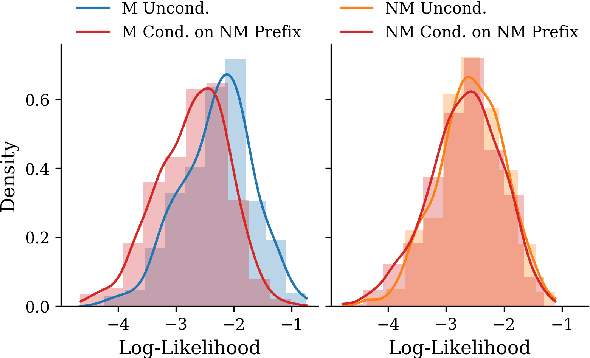
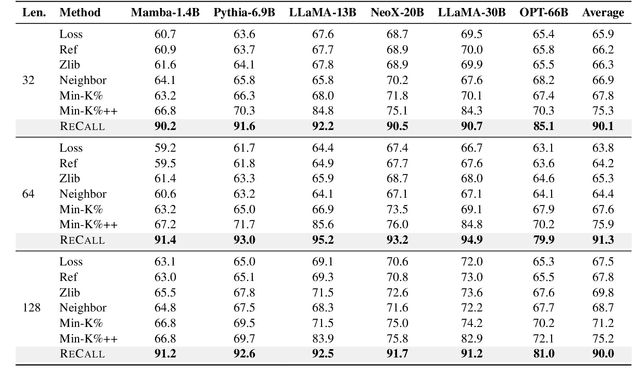
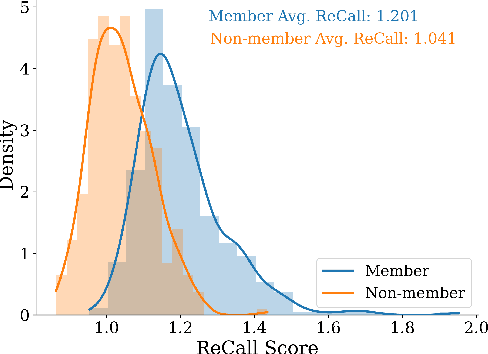
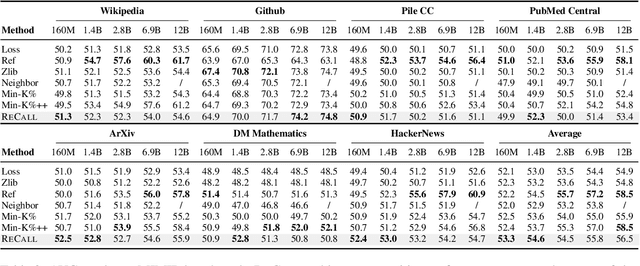
Abstract:The rapid scaling of large language models (LLMs) has raised concerns about the transparency and fair use of the pretraining data used for training them. Detecting such content is challenging due to the scale of the data and limited exposure of each instance during training. We propose ReCaLL (Relative Conditional Log-Likelihood), a novel membership inference attack (MIA) to detect LLMs' pretraining data by leveraging their conditional language modeling capabilities. ReCaLL examines the relative change in conditional log-likelihoods when prefixing target data points with non-member context. Our empirical findings show that conditioning member data on non-member prefixes induces a larger decrease in log-likelihood compared to non-member data. We conduct comprehensive experiments and show that ReCaLL achieves state-of-the-art performance on the WikiMIA dataset, even with random and synthetic prefixes, and can be further improved using an ensemble approach. Moreover, we conduct an in-depth analysis of LLMs' behavior with different membership contexts, providing insights into how LLMs leverage membership information for effective inference at both the sequence and token level.
Randomized Greedy Algorithms and Composable Coreset for k-Center Clustering with Outliers
Jan 07, 2023Abstract:In this paper, we study the problem of {\em $k$-center clustering with outliers}. The problem has many important applications in real world, but the presence of outliers can significantly increase the computational complexity. Though a number of methods have been developed in the past decades, it is still quite challenging to design quality guaranteed algorithm with low complexity for this problem. Our idea is inspired by the greedy method, Gonzalez's algorithm, that was developed for solving the ordinary $k$-center clustering problem. Based on some novel observations, we show that a simple randomized version of this greedy strategy actually can handle outliers efficiently. We further show that this randomized greedy approach also yields small coreset for the problem in doubling metrics (even if the doubling dimension is not given), which can greatly reduce the computational complexity. Moreover, together with the partial clustering framework proposed in arXiv:1703.01539 , we prove that our coreset method can be applied to distributed data with a low communication complexity. The experimental results suggest that our algorithms can achieve near optimal solutions and yield lower complexities comparing with the existing methods.
Coresets for Relational Data and The Applications
Oct 09, 2022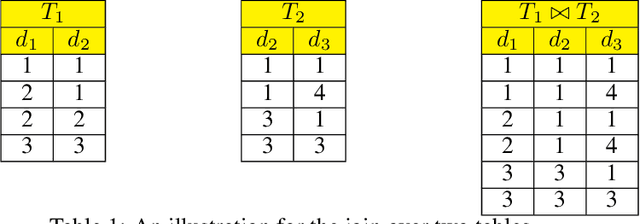
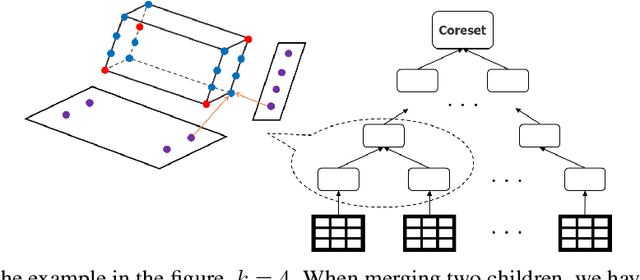
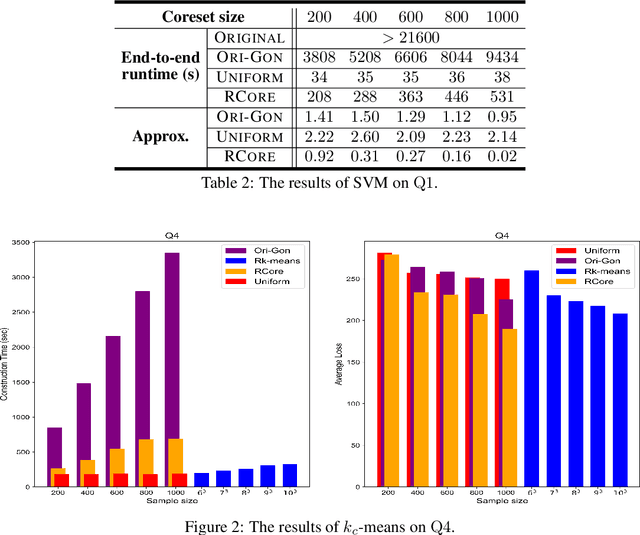
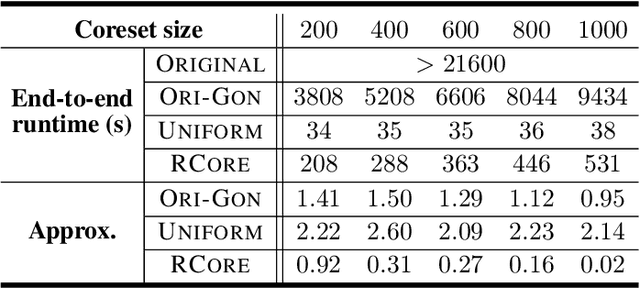
Abstract:A coreset is a small set that can approximately preserve the structure of the original input data set. Therefore we can run our algorithm on a coreset so as to reduce the total computational complexity. Conventional coreset techniques assume that the input data set is available to process explicitly. However, this assumption may not hold in real-world scenarios. In this paper, we consider the problem of coresets construction over relational data. Namely, the data is decoupled into several relational tables, and it could be very expensive to directly materialize the data matrix by joining the tables. We propose a novel approach called ``aggregation tree with pseudo-cube'' that can build a coreset from bottom to up. Moreover, our approach can neatly circumvent several troublesome issues of relational learning problems [Khamis et al., PODS 2019]. Under some mild assumptions, we show that our coreset approach can be applied for the machine learning tasks, such as clustering, logistic regression and SVM.
Coresets for Wasserstein Distributionally Robust Optimization Problems
Oct 09, 2022
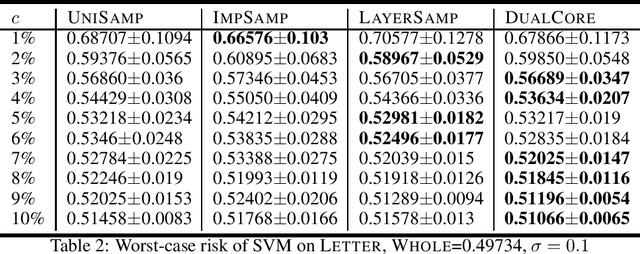
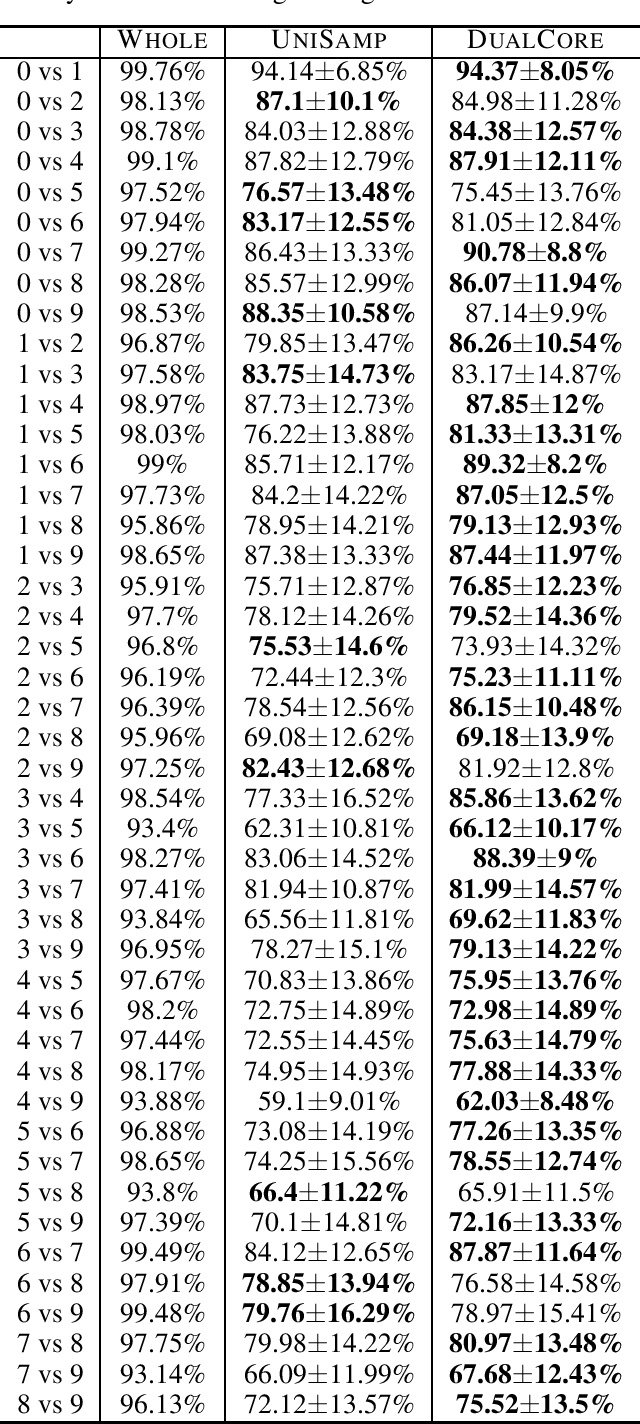
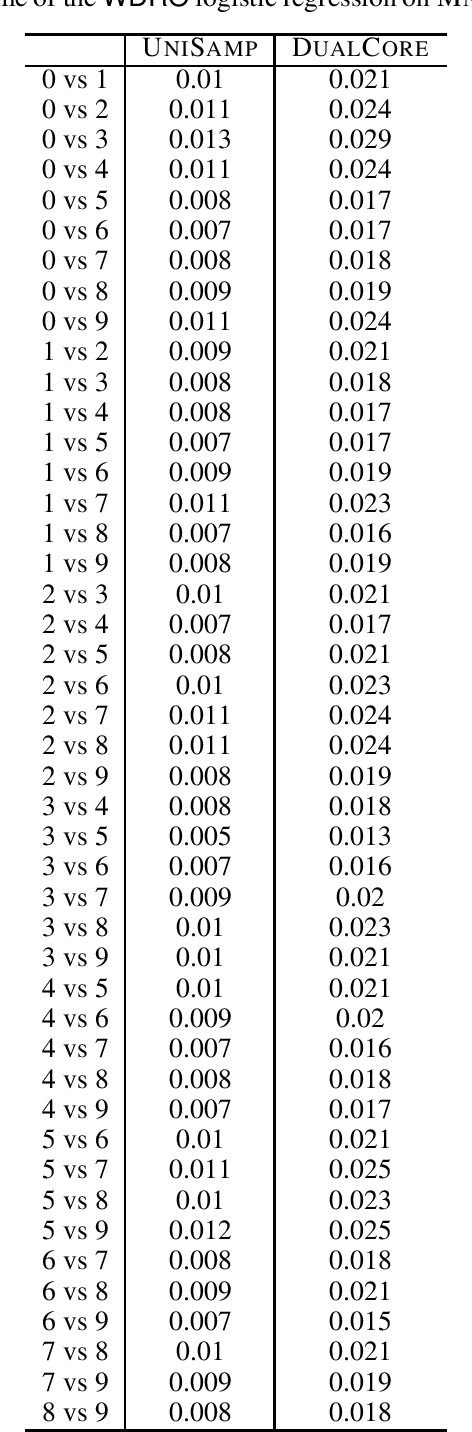
Abstract:Wasserstein distributionally robust optimization (\textsf{WDRO}) is a popular model to enhance the robustness of machine learning with ambiguous data. However, the complexity of \textsf{WDRO} can be prohibitive in practice since solving its ``minimax'' formulation requires a great amount of computation. Recently, several fast \textsf{WDRO} training algorithms for some specific machine learning tasks (e.g., logistic regression) have been developed. However, the research on designing efficient algorithms for general large-scale \textsf{WDRO}s is still quite limited, to the best of our knowledge. \textit{Coreset} is an important tool for compressing large dataset, and thus it has been widely applied to reduce the computational complexities for many optimization problems. In this paper, we introduce a unified framework to construct the $\epsilon$-coreset for the general \textsf{WDRO} problems. Though it is challenging to obtain a conventional coreset for \textsf{WDRO} due to the uncertainty issue of ambiguous data, we show that we can compute a ``dual coreset'' by using the strong duality property of \textsf{WDRO}. Also, the error introduced by the dual coreset can be theoretically guaranteed for the original \textsf{WDRO} objective. To construct the dual coreset, we propose a novel grid sampling approach that is particularly suitable for the dual formulation of \textsf{WDRO}. Finally, we implement our coreset approach and illustrate its effectiveness for several \textsf{WDRO} problems in the experiments.
A Novel Sequential Coreset Method for Gradient Descent Algorithms
Dec 05, 2021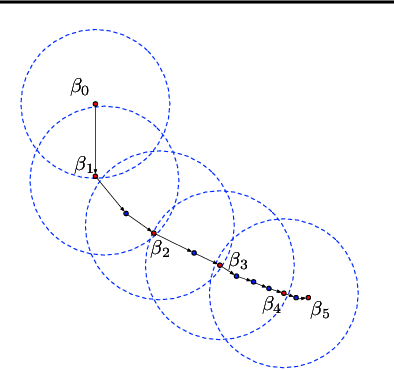
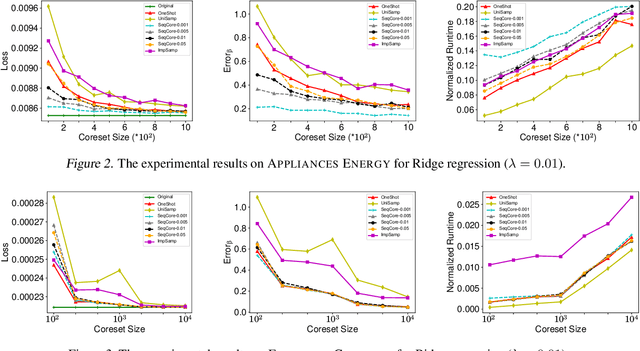

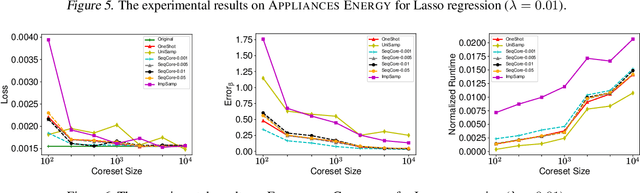
Abstract:A wide range of optimization problems arising in machine learning can be solved by gradient descent algorithms, and a central question in this area is how to efficiently compress a large-scale dataset so as to reduce the computational complexity. {\em Coreset} is a popular data compression technique that has been extensively studied before. However, most of existing coreset methods are problem-dependent and cannot be used as a general tool for a broader range of applications. A key obstacle is that they often rely on the pseudo-dimension and total sensitivity bound that can be very high or hard to obtain. In this paper, based on the ''locality'' property of gradient descent algorithms, we propose a new framework, termed ''sequential coreset'', which effectively avoids these obstacles. Moreover, our method is particularly suitable for sparse optimization whence the coreset size can be further reduced to be only poly-logarithmically dependent on the dimension. In practice, the experimental results suggest that our method can save a large amount of running time compared with the baseline algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge