Qingyuan Yang
FRWKV:Frequency-Domain Linear Attention for Long-Term Time Series Forecasting
Dec 09, 2025Abstract:Traditional Transformers face a major bottleneck in long-sequence time series forecasting due to their quadratic complexity $(\mathcal{O}(T^2))$ and their limited ability to effectively exploit frequency-domain information. Inspired by RWKV's $\mathcal{O}(T)$ linear attention and frequency-domain modeling, we propose FRWKV, a frequency-domain linear-attention framework that overcomes these limitations. Our model integrates linear attention mechanisms with frequency-domain analysis, achieving $\mathcal{O}(T)$ computational complexity in the attention path while exploiting spectral information to enhance temporal feature representations for scalable long-sequence modeling. Across eight real-world datasets, FRWKV achieves a first-place average rank. Our ablation studies confirm the critical roles of both the linear attention and frequency-encoder components. This work demonstrates the powerful synergy between linear attention and frequency analysis, establishing a new paradigm for scalable time series modeling. Code is available at this repository: https://github.com/yangqingyuan-byte/FRWKV.
MSSDF: Modality-Shared Self-supervised Distillation for High-Resolution Multi-modal Remote Sensing Image Learning
Jun 11, 2025
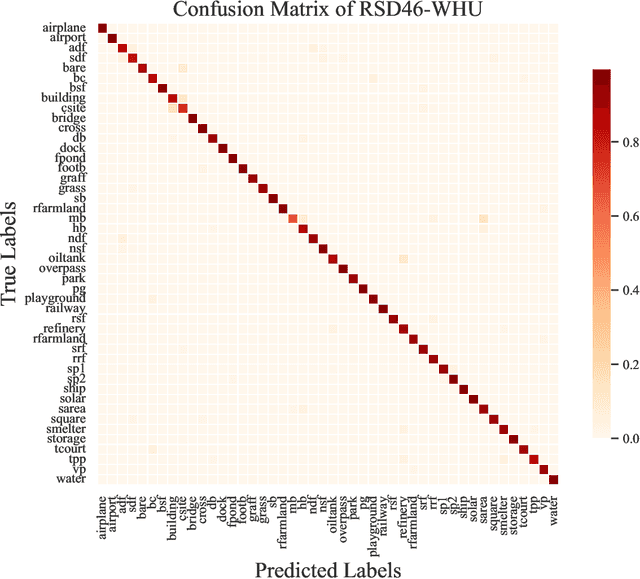
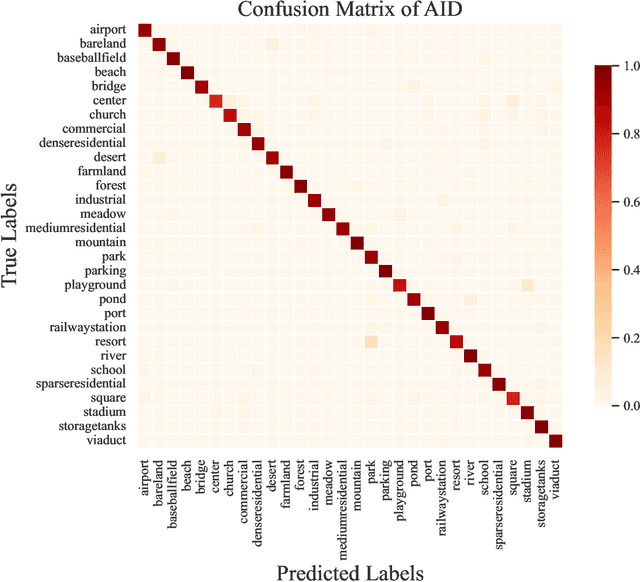
Abstract:Remote sensing image interpretation plays a critical role in environmental monitoring, urban planning, and disaster assessment. However, acquiring high-quality labeled data is often costly and time-consuming. To address this challenge, we proposes a multi-modal self-supervised learning framework that leverages high-resolution RGB images, multi-spectral data, and digital surface models (DSM) for pre-training. By designing an information-aware adaptive masking strategy, cross-modal masking mechanism, and multi-task self-supervised objectives, the framework effectively captures both the correlations across different modalities and the unique feature structures within each modality. We evaluated the proposed method on multiple downstream tasks, covering typical remote sensing applications such as scene classification, semantic segmentation, change detection, object detection, and depth estimation. Experiments are conducted on 15 remote sensing datasets, encompassing 26 tasks. The results demonstrate that the proposed method outperforms existing pretraining approaches in most tasks. Specifically, on the Potsdam and Vaihingen semantic segmentation tasks, our method achieved mIoU scores of 78.30\% and 76.50\%, with only 50\% train-set. For the US3D depth estimation task, the RMSE error is reduced to 0.182, and for the binary change detection task in SECOND dataset, our method achieved mIoU scores of 47.51\%, surpassing the second CS-MAE by 3 percentage points. Our pretrain code, checkpoints, and HR-Pairs dataset can be found in https://github.com/CVEO/MSSDF.
Relax and Merge: A Simple Yet Effective Framework for Solving Fair $k$-Means and $k$-sparse Wasserstein Barycenter Problems
Nov 02, 2024Abstract:The fairness of clustering algorithms has gained widespread attention across various areas, including machine learning, In this paper, we study fair $k$-means clustering in Euclidean space. Given a dataset comprising several groups, the fairness constraint requires that each cluster should contain a proportion of points from each group within specified lower and upper bounds. Due to these fairness constraints, determining the optimal locations of $k$ centers is a quite challenging task. We propose a novel ``Relax and Merge'' framework that returns a $(1+4\rho + O(\epsilon))$-approximate solution, where $\rho$ is the approximate ratio of an off-the-shelf vanilla $k$-means algorithm and $O(\epsilon)$ can be an arbitrarily small positive number. If equipped with a PTAS of $k$-means, our solution can achieve an approximation ratio of $(5+O(\epsilon))$ with only a slight violation of the fairness constraints, which improves the current state-of-the-art approximation guarantee. Furthermore, using our framework, we can also obtain a $(1+4\rho +O(\epsilon))$-approximate solution for the $k$-sparse Wasserstein Barycenter problem, which is a fundamental optimization problem in the field of optimal transport, and a $(2+6\rho)$-approximate solution for the strictly fair $k$-means clustering with no violation, both of which are better than the current state-of-the-art methods. In addition, the empirical results demonstrate that our proposed algorithm can significantly outperform baseline approaches in terms of clustering cost.
Approximate Algorithms For $k$-Sparse Wasserstein Barycenter With Outliers
Apr 20, 2024Abstract:Wasserstein Barycenter (WB) is one of the most fundamental optimization problems in optimal transportation. Given a set of distributions, the goal of WB is to find a new distribution that minimizes the average Wasserstein distance to them. The problem becomes even harder if we restrict the solution to be ``$k$-sparse''. In this paper, we study the $k$-sparse WB problem in the presence of outliers, which is a more practical setting since real-world data often contains noise. Existing WB algorithms cannot be directly extended to handle the case with outliers, and thus it is urgently needed to develop some novel ideas. First, we investigate the relation between $k$-sparse WB with outliers and the clustering (with outliers) problems. In particular, we propose a clustering based LP method that yields constant approximation factor for the $k$-sparse WB with outliers problem. Further, we utilize the coreset technique to achieve the $(1+\epsilon)$-approximation factor for any $\epsilon>0$, if the dimensionality is not high. Finally, we conduct the experiments for our proposed algorithms and illustrate their efficiencies in practice.
S3Net: Innovating Stereo Matching and Semantic Segmentation with a Single-Branch Semantic Stereo Network in Satellite Epipolar Imagery
Jan 03, 2024



Abstract:Stereo matching and semantic segmentation are significant tasks in binocular satellite 3D reconstruction. However, previous studies primarily view these as independent parallel tasks, lacking an integrated multitask learning framework. This work introduces a solution, the Single-branch Semantic Stereo Network (S3Net), which innovatively combines semantic segmentation and stereo matching using Self-Fuse and Mutual-Fuse modules. Unlike preceding methods that utilize semantic or disparity information independently, our method dentifies and leverages the intrinsic link between these two tasks, leading to a more accurate understanding of semantic information and disparity estimation. Comparative testing on the US3D dataset proves the effectiveness of our S3Net. Our model improves the mIoU in semantic segmentation from 61.38 to 67.39, and reduces the D1-Error and average endpoint error (EPE) in disparity estimation from 10.051 to 9.579 and 1.439 to 1.403 respectively, surpassing existing competitive methods. Our codes are available at:https://github.com/CVEO/S3Net.
On Robust Wasserstein Barycenter: The Model and Algorithm
Dec 25, 2023Abstract:The Wasserstein barycenter problem is to compute the average of $m$ given probability measures, which has been widely studied in many different areas; however, real-world data sets are often noisy and huge, which impedes its applications in practice. Hence, in this paper, we focus on improving the computational efficiency of two types of robust Wasserstein barycenter problem (RWB): fixed-support RWB (fixed-RWB) and free-support RWB (free-RWB); actually, the former is a subroutine of the latter. Firstly, we improve efficiency through model reducing; we reduce RWB as an augmented Wasserstein barycenter problem, which works for both fixed-RWB and free-RWB. Especially, fixed-RWB can be computed within $\widetilde{O}(\frac{mn^2}{\epsilon_+})$ time by using an off-the-shelf solver, where $\epsilon_+$ is the pre-specified additive error and $n$ is the size of locations of input measures. Then, for free-RWB, we leverage a quality guaranteed data compression technique, coreset, to accelerate computation by reducing the data set size $m$. It shows that running algorithms on the coreset is enough instead of on the original data set. Next, by combining the model reducing and coreset techniques above, we propose an algorithm for free-RWB by updating the weights and locations alternatively. Finally, our experiments demonstrate the efficiency of our techniques.
Coresets for Relational Data and The Applications
Oct 09, 2022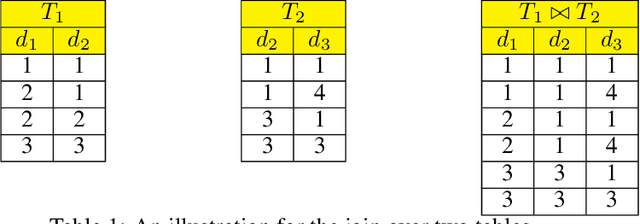
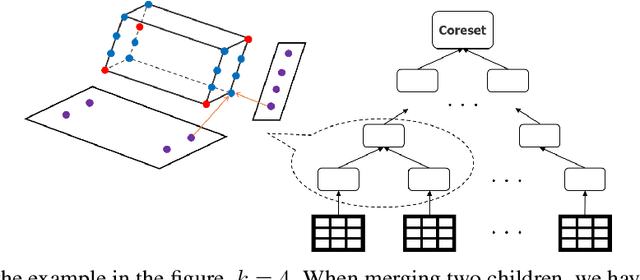
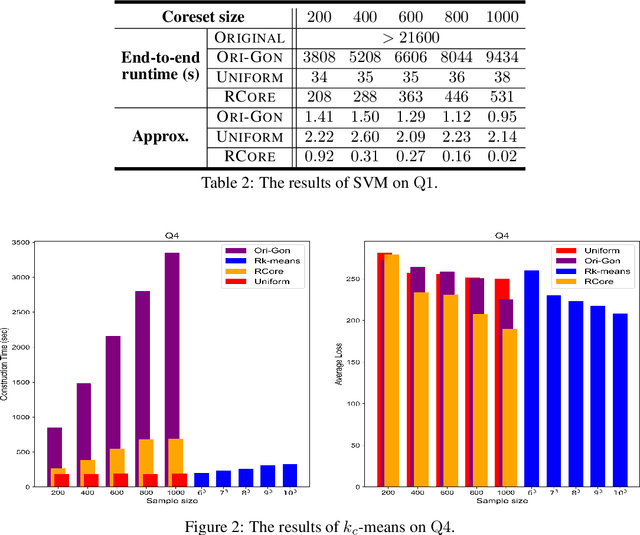
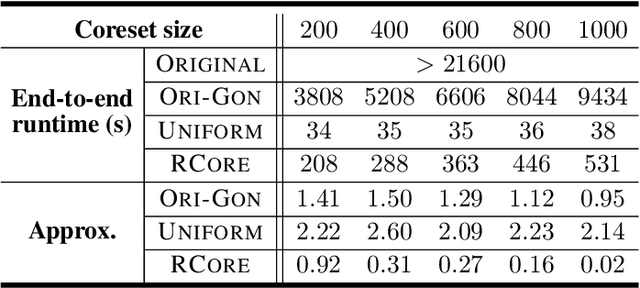
Abstract:A coreset is a small set that can approximately preserve the structure of the original input data set. Therefore we can run our algorithm on a coreset so as to reduce the total computational complexity. Conventional coreset techniques assume that the input data set is available to process explicitly. However, this assumption may not hold in real-world scenarios. In this paper, we consider the problem of coresets construction over relational data. Namely, the data is decoupled into several relational tables, and it could be very expensive to directly materialize the data matrix by joining the tables. We propose a novel approach called ``aggregation tree with pseudo-cube'' that can build a coreset from bottom to up. Moreover, our approach can neatly circumvent several troublesome issues of relational learning problems [Khamis et al., PODS 2019]. Under some mild assumptions, we show that our coreset approach can be applied for the machine learning tasks, such as clustering, logistic regression and SVM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge