Relax and Merge: A Simple Yet Effective Framework for Solving Fair $k$-Means and $k$-sparse Wasserstein Barycenter Problems

The fairness of clustering algorithms has gained widespread attention across various areas, including machine learning, In this paper, we study fair $k$-means clustering in Euclidean space. Given a dataset comprising several groups, the fairness constraint requires that each cluster should contain a proportion of points from each group within specified lower and upper bounds. Due to these fairness constraints, determining the optimal locations of $k$ centers is a quite challenging task. We propose a novel ``Relax and Merge'' framework that returns a $(1+4\rho + O(\epsilon))$-approximate solution, where $\rho$ is the approximate ratio of an off-the-shelf vanilla $k$-means algorithm and $O(\epsilon)$ can be an arbitrarily small positive number. If equipped with a PTAS of $k$-means, our solution can achieve an approximation ratio of $(5+O(\epsilon))$ with only a slight violation of the fairness constraints, which improves the current state-of-the-art approximation guarantee. Furthermore, using our framework, we can also obtain a $(1+4\rho +O(\epsilon))$-approximate solution for the $k$-sparse Wasserstein Barycenter problem, which is a fundamental optimization problem in the field of optimal transport, and a $(2+6\rho)$-approximate solution for the strictly fair $k$-means clustering with no violation, both of which are better than the current state-of-the-art methods. In addition, the empirical results demonstrate that our proposed algorithm can significantly outperform baseline approaches in terms of clustering cost.

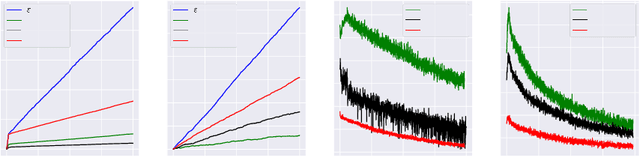
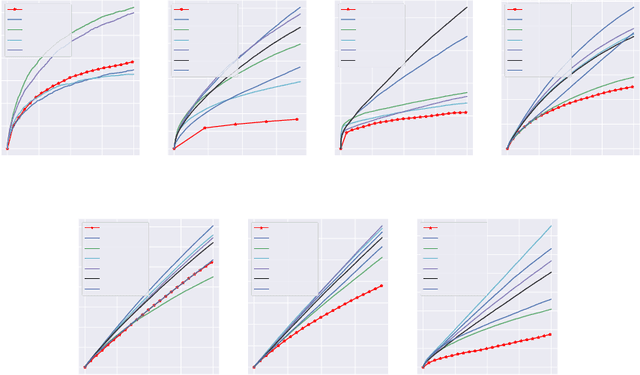
Regularized OFU: an Efficient UCB Estimator forNon-linear Contextual Bandit

Balancing exploration and exploitation (EE) is a fundamental problem in contex-tual bandit. One powerful principle for EE trade-off isOptimism in Face of Uncer-tainty(OFU), in which the agent takes the action according to an upper confidencebound (UCB) of reward. OFU has achieved (near-)optimal regret bound for lin-ear/kernel contextual bandits. However, it is in general unknown how to deriveefficient and effective EE trade-off methods for non-linearcomplex tasks, suchas contextual bandit with deep neural network as the reward function. In thispaper, we propose a novel OFU algorithm namedregularized OFU(ROFU). InROFU, we measure the uncertainty of the reward by a differentiable function andcompute the upper confidence bound by solving a regularized optimization prob-lem. We prove that, for multi-armed bandit, kernel contextual bandit and neuraltangent kernel bandit, ROFU achieves (near-)optimal regret bounds with certainuncertainty measure, which theoretically justifies its effectiveness on EE trade-off.Importantly, ROFU admits a very efficient implementation with gradient-basedoptimizer, which easily extends to general deep neural network models beyondneural tangent kernel, in sharp contrast with previous OFU methods. The em-pirical evaluation demonstrates that ROFU works extremelywell for contextualbandits under various settings.

Understanding Human Behaviors in Crowds by Imitating the Decision-Making Process

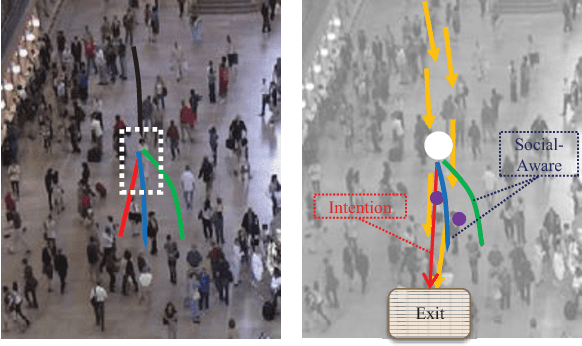
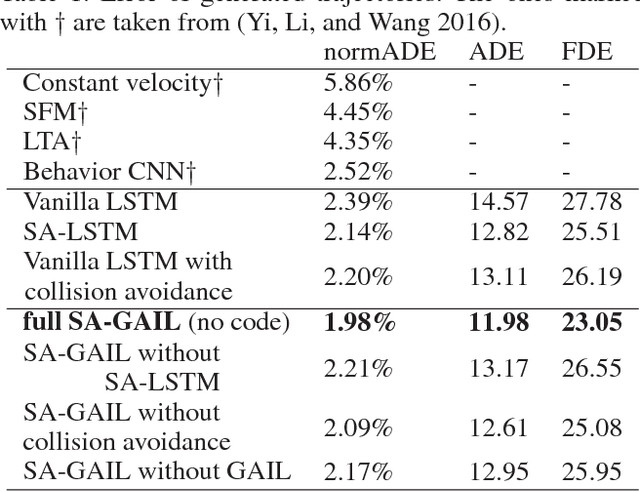
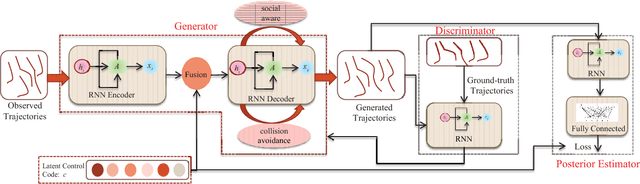
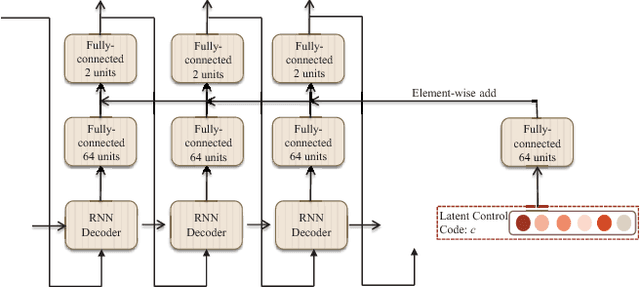
Crowd behavior understanding is crucial yet challenging across a wide range of applications, since crowd behavior is inherently determined by a sequential decision-making process based on various factors, such as the pedestrians' own destinations, interaction with nearby pedestrians and anticipation of upcoming events. In this paper, we propose a novel framework of Social-Aware Generative Adversarial Imitation Learning (SA-GAIL) to mimic the underlying decision-making process of pedestrians in crowds. Specifically, we infer the latent factors of human decision-making process in an unsupervised manner by extending the Generative Adversarial Imitation Learning framework to anticipate future paths of pedestrians. Different factors of human decision making are disentangled with mutual information maximization, with the process modeled by collision avoidance regularization and Social-Aware LSTMs. Experimental results demonstrate the potential of our framework in disentangling the latent decision-making factors of pedestrians and stronger abilities in predicting future trajectories.