Stabilizing Policy Gradients for Stochastic Differential Equations via Consistency with Perturbation Process

Considering generating samples with high rewards, we focus on optimizing deep neural networks parameterized stochastic differential equations (SDEs), the advanced generative models with high expressiveness, with policy gradient, the leading algorithm in reinforcement learning. Nevertheless, when applying policy gradients to SDEs, since the policy gradient is estimated on a finite set of trajectories, it can be ill-defined, and the policy behavior in data-scarce regions may be uncontrolled. This challenge compromises the stability of policy gradients and negatively impacts sample complexity. To address these issues, we propose constraining the SDE to be consistent with its associated perturbation process. Since the perturbation process covers the entire space and is easy to sample, we can mitigate the aforementioned problems. Our framework offers a general approach allowing for a versatile selection of policy gradient methods to effectively and efficiently train SDEs. We evaluate our algorithm on the task of structure-based drug design and optimize the binding affinity of generated ligand molecules. Our method achieves the best Vina score -9.07 on the CrossDocked2020 dataset.

Simultaneously Learning Stochastic and Adversarial Bandits with General Graph Feedback

The problem of online learning with graph feedback has been extensively studied in the literature due to its generality and potential to model various learning tasks. Existing works mainly study the adversarial and stochastic feedback separately. If the prior knowledge of the feedback mechanism is unavailable or wrong, such specially designed algorithms could suffer great loss. To avoid this problem, \citet{erez2021towards} try to optimize for both environments. However, they assume the feedback graphs are undirected and each vertex has a self-loop, which compromises the generality of the framework and may not be satisfied in applications. With a general feedback graph, the observation of an arm may not be available when this arm is pulled, which makes the exploration more expensive and the algorithms more challenging to perform optimally in both environments. In this work, we overcome this difficulty by a new trade-off mechanism with a carefully-designed proportion for exploration and exploitation. We prove the proposed algorithm simultaneously achieves $\mathrm{poly} \log T$ regret in the stochastic setting and minimax-optimal regret of $\tilde{O}(T^{2/3})$ in the adversarial setting where $T$ is the horizon and $\tilde{O}$ hides parameters independent of $T$ as well as logarithmic terms. To our knowledge, this is the first best-of-both-worlds result for general feedback graphs.

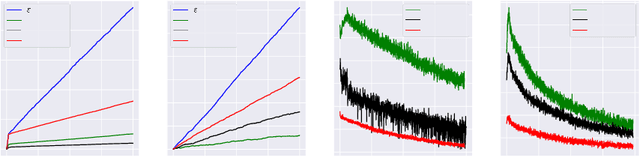
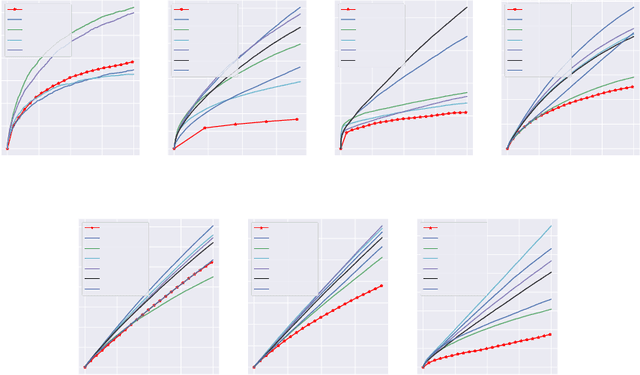
Regularized OFU: an Efficient UCB Estimator forNon-linear Contextual Bandit

Balancing exploration and exploitation (EE) is a fundamental problem in contex-tual bandit. One powerful principle for EE trade-off isOptimism in Face of Uncer-tainty(OFU), in which the agent takes the action according to an upper confidencebound (UCB) of reward. OFU has achieved (near-)optimal regret bound for lin-ear/kernel contextual bandits. However, it is in general unknown how to deriveefficient and effective EE trade-off methods for non-linearcomplex tasks, suchas contextual bandit with deep neural network as the reward function. In thispaper, we propose a novel OFU algorithm namedregularized OFU(ROFU). InROFU, we measure the uncertainty of the reward by a differentiable function andcompute the upper confidence bound by solving a regularized optimization prob-lem. We prove that, for multi-armed bandit, kernel contextual bandit and neuraltangent kernel bandit, ROFU achieves (near-)optimal regret bounds with certainuncertainty measure, which theoretically justifies its effectiveness on EE trade-off.Importantly, ROFU admits a very efficient implementation with gradient-basedoptimizer, which easily extends to general deep neural network models beyondneural tangent kernel, in sharp contrast with previous OFU methods. The em-pirical evaluation demonstrates that ROFU works extremelywell for contextualbandits under various settings.

Lazy-CFR: a fast regret minimization algorithm for extensive games with imperfect information

In this paper, we focus on solving two-player zero-sum extensive games with imperfect information. Counterfactual regret minimization (CFR) is the most popular algorithm on solving such games and achieves state-of-the-art performance in practice. However, the performance of CFR is not fully understood, since empirical results on the regret are much better than the upper bound proved in \cite{zinkevich2008regret}. Another issue of CFR is that CFR has to traverse the whole game tree in each round, which is not tolerable in large scale games. In this paper, we present a novel technique, lazy update, which can avoid traversing the whole game tree in CFR. Further, we present a novel analysis on the CFR with lazy update. Our analysis can also be applied to the vanilla CFR, which results in a much tighter regret bound than that proved in \cite{zinkevich2008regret}. Inspired by lazy update, we further present a novel CFR variant, named Lazy-CFR. Compared to traversing $O(|\mathcal{I}|)$ information sets in vanilla CFR, Lazy-CFR needs only to traverse $O(\sqrt{|\mathcal{I}|})$ information sets per round while the regret bound almost keep the same, where $\mathcal{I}$ is the class of all information sets. As a result, Lazy-CFR shows better convergence result compared with vanilla CFR. Experimental results consistently show that Lazy-CFR outperforms the vanilla CFR significantly.

Label Aggregation via Finding Consensus Between Models

Label aggregation is an efficient and low cost way to make large datasets for supervised learning. It takes the noisy labels provided by non-experts and infers the unknown true labels. In this paper, we propose a novel label aggregation algorithm which includes a label aggregation neural network. The learning task in this paper is unsupervised. In order to train the neural network, we try to design a suitable guiding model to define the loss function. The optimization goal of our algorithm is to find the consensus between the predictions of the neural network and the guiding model. This algorithm is easy to optimize using mini-batch stochastic optimization methods. Since the choices of the neural network and the guiding model are very flexible, our label aggregation algorithm is easy to extend. According to the algorithm framework, we design two novel models to aggregate noisy labels. Experimental results show that our models achieve better results than state-of-the-art label aggregation methods.

Racing Thompson: an Efficient Algorithm for Thompson Sampling with Non-conjugate Priors

Thompson sampling has impressive empirical performance for many multi-armed bandit problems. But current algorithms for Thompson sampling only work for the case of conjugate priors since these algorithms require to infer the posterior, which is often computationally intractable when the prior is not conjugate. In this paper, we propose a novel algorithm for Thompson sampling which only requires to draw samples from a tractable distribution, so our algorithm is efficient even when the prior is non-conjugate. To do this, we reformulate Thompson sampling as an optimization problem via the Gumbel-Max trick. After that we construct a set of random variables and our goal is to identify the one with highest mean. Finally, we solve it with techniques in best arm identification.