Fang Kong
Hybrid Combinatorial Multi-armed Bandits with Probabilistically Triggered Arms
Dec 26, 2025Abstract:The problem of combinatorial multi-armed bandits with probabilistically triggered arms (CMAB-T) has been extensively studied. Prior work primarily focuses on either the online setting where an agent learns about the unknown environment through iterative interactions, or the offline setting where a policy is learned solely from logged data. However, each of these paradigms has inherent limitations: online algorithms suffer from high interaction costs and slow adaptation, while offline methods are constrained by dataset quality and lack of exploration capabilities. To address these complementary weaknesses, we propose hybrid CMAB-T, a new framework that integrates offline data with online interaction in a principled manner. Our proposed hybrid CUCB algorithm leverages offline data to guide exploration and accelerate convergence, while strategically incorporating online interactions to mitigate the insufficient coverage or distributional bias of the offline dataset. We provide theoretical guarantees on the algorithm's regret, demonstrating that hybrid CUCB significantly outperforms purely online approaches when high-quality offline data is available, and effectively corrects the bias inherent in offline-only methods when the data is limited or misaligned. Empirical results further demonstrate the consistent advantage of our algorithm.
Toward Real-World Chinese Psychological Support Dialogues: CPsDD Dataset and a Co-Evolving Multi-Agent System
Jul 10, 2025
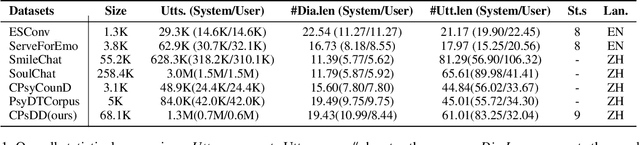
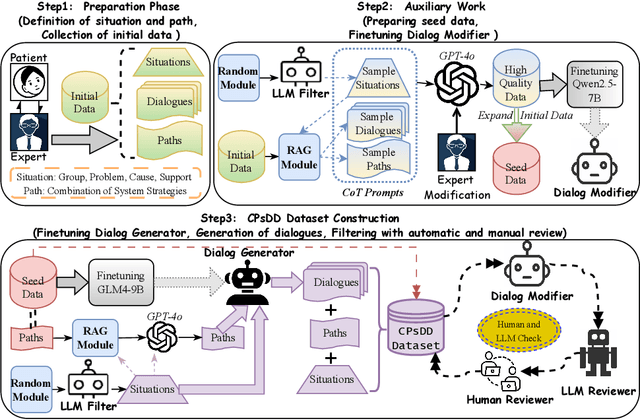
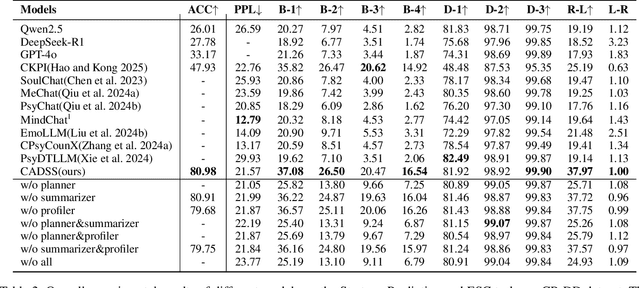
Abstract:The growing need for psychological support due to increasing pressures has exposed the scarcity of relevant datasets, particularly in non-English languages. To address this, we propose a framework that leverages limited real-world data and expert knowledge to fine-tune two large language models: Dialog Generator and Dialog Modifier. The Generator creates large-scale psychological counseling dialogues based on predefined paths, which guide system response strategies and user interactions, forming the basis for effective support. The Modifier refines these dialogues to align with real-world data quality. Through both automated and manual review, we construct the Chinese Psychological support Dialogue Dataset (CPsDD), containing 68K dialogues across 13 groups, 16 psychological problems, 13 causes, and 12 support focuses. Additionally, we introduce the Comprehensive Agent Dialogue Support System (CADSS), where a Profiler analyzes user characteristics, a Summarizer condenses dialogue history, a Planner selects strategies, and a Supporter generates empathetic responses. The experimental results of the Strategy Prediction and Emotional Support Conversation (ESC) tasks demonstrate that CADSS achieves state-of-the-art performance on both CPsDD and ESConv datasets.
Multi-Hop Question Generation via Dual-Perspective Keyword Guidance
May 21, 2025Abstract:Multi-hop question generation (MQG) aims to generate questions that require synthesizing multiple information snippets from documents to derive target answers. The primary challenge lies in effectively pinpointing crucial information snippets related to question-answer (QA) pairs, typically relying on keywords. However, existing works fail to fully utilize the guiding potential of keywords and neglect to differentiate the distinct roles of question-specific and document-specific keywords. To address this, we define dual-perspective keywords (i.e., question and document keywords) and propose a Dual-Perspective Keyword-Guided (DPKG) framework, which seamlessly integrates keywords into the multi-hop question generation process. We argue that question keywords capture the questioner's intent, whereas document keywords reflect the content related to the QA pair. Functionally, question and document keywords work together to pinpoint essential information snippets in the document, with question keywords required to appear in the generated question. The DPKG framework consists of an expanded transformer encoder and two answer-aware transformer decoders for keyword and question generation, respectively. Extensive experiments demonstrate the effectiveness of our work, showcasing its promising performance and underscoring its significant value in the MQG task.
Impact of Stickers on Multimodal Chat Sentiment Analysis and Intent Recognition: A New Task, Dataset and Baseline
May 14, 2024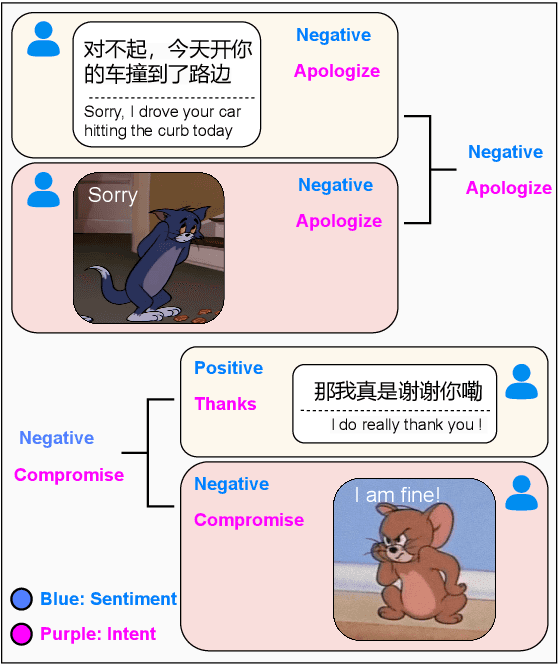
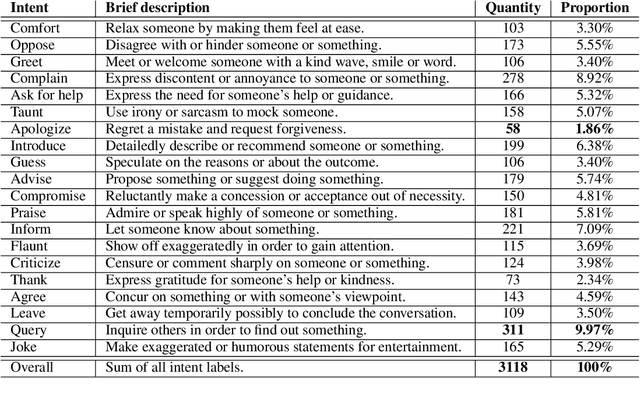
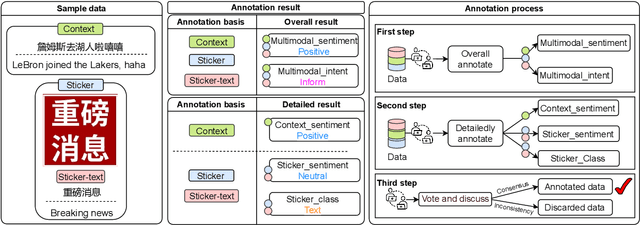
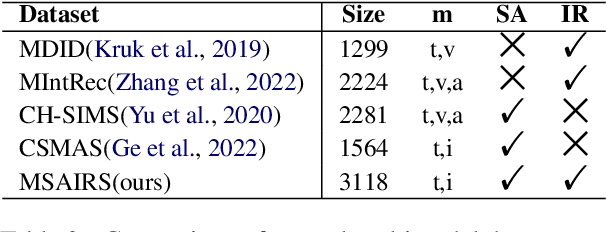
Abstract:Stickers are increasingly used in social media to express sentiment and intent. When finding typing troublesome, people often use a sticker instead. Despite the significant impact of stickers on sentiment analysis and intent recognition, little research has been conducted. To address this gap, we propose a new task: Multimodal chat Sentiment Analysis and Intent Recognition involving Stickers (MSAIRS). Additionally, we introduce a novel multimodal dataset containing Chinese chat records and stickers excerpted from several mainstream social media platforms. Our dataset includes paired data with the same text but different stickers, and various stickers consisting of the same images with different texts, allowing us to better understand the impact of stickers on chat sentiment and intent. We also propose an effective multimodal joint model, MMSAIR, for our task, which is validated on our datasets and indicates that visual information of stickers counts. Our dataset and code will be publicly available.
Which LLM to Play? Convergence-Aware Online Model Selection with Time-Increasing Bandits
Mar 11, 2024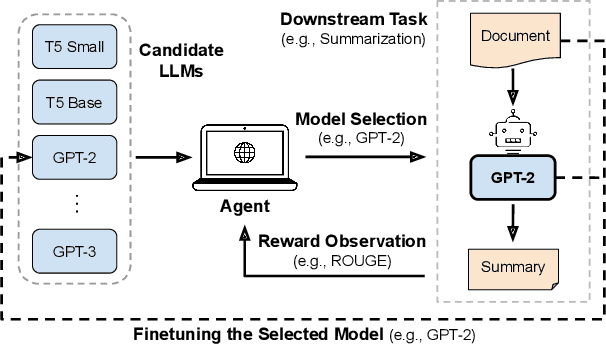

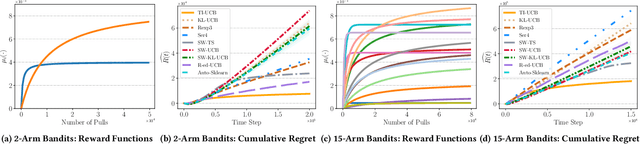
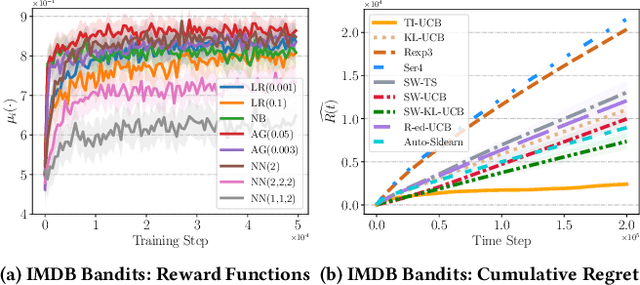
Abstract:Web-based applications such as chatbots, search engines and news recommendations continue to grow in scale and complexity with the recent surge in the adoption of LLMs. Online model selection has thus garnered increasing attention due to the need to choose the best model among a diverse set while balancing task reward and exploration cost. Organizations faces decisions like whether to employ a costly API-based LLM or a locally finetuned small LLM, weighing cost against performance. Traditional selection methods often evaluate every candidate model before choosing one, which are becoming impractical given the rising costs of training and finetuning LLMs. Moreover, it is undesirable to allocate excessive resources towards exploring poor-performing models. While some recent works leverage online bandit algorithm to manage such exploration-exploitation trade-off in model selection, they tend to overlook the increasing-then-converging trend in model performances as the model is iteratively finetuned, leading to less accurate predictions and suboptimal model selections. In this paper, we propose a time-increasing bandit algorithm TI-UCB, which effectively predicts the increase of model performances due to finetuning and efficiently balances exploration and exploitation in model selection. To further capture the converging points of models, we develop a change detection mechanism by comparing consecutive increase predictions. We theoretically prove that our algorithm achieves a logarithmic regret upper bound in a typical increasing bandit setting, which implies a fast convergence rate. The advantage of our method is also empirically validated through extensive experiments on classification model selection and online selection of LLMs. Our results highlight the importance of utilizing increasing-then-converging pattern for more efficient and economic model selection in the deployment of LLMs.
Improved Bandits in Many-to-one Matching Markets with Incentive Compatibility
Jan 03, 2024
Abstract:Two-sided matching markets have been widely studied in the literature due to their rich applications. Since participants are usually uncertain about their preferences, online algorithms have recently been adopted to learn them through iterative interactions. \citet{wang2022bandit} initiate the study of this problem in a many-to-one setting with \textit{responsiveness}. However, their results are far from optimal and lack guarantees of incentive compatibility. An extension of \citet{kong2023player} to this more general setting achieves a near-optimal bound for player-optimal regret. Nevertheless, due to the substantial requirement for collaboration, a single player's deviation could lead to a huge increase in its own cumulative rewards and an $O(T)$ regret for others. In this paper, we aim to enhance the regret bound in many-to-one markets while ensuring incentive compatibility. We first propose the adaptively explore-then-deferred-acceptance (AETDA) algorithm for responsiveness setting and derive an $O(N\min\left\{N,K\right\}C\log T/\Delta^2)$ upper bound for player-optimal stable regret while demonstrating its guarantee of incentive compatibility, where $N$ represents the number of players, $K$ is the number of arms, $T$ denotes the time horizon, $C$ is arms' total capacities and $\Delta$ signifies the minimum preference gap among players. This result is a significant improvement over \citet{wang2022bandit}. And to the best of our knowledge, it constitutes the first player-optimal guarantee in matching markets that offers such robust assurances. We also consider broader \textit{substitutable} preferences, one of the most general conditions to ensure the existence of a stable matching and cover responsiveness. We devise an online DA (ODA) algorithm and establish an $O(NK\log T/\Delta^2)$ player-pessimal stable regret bound for this setting.
Player-optimal Stable Regret for Bandit Learning in Matching Markets
Jul 20, 2023Abstract:The problem of matching markets has been studied for a long time in the literature due to its wide range of applications. Finding a stable matching is a common equilibrium objective in this problem. Since market participants are usually uncertain of their preferences, a rich line of recent works study the online setting where one-side participants (players) learn their unknown preferences from iterative interactions with the other side (arms). Most previous works in this line are only able to derive theoretical guarantees for player-pessimal stable regret, which is defined compared with the players' least-preferred stable matching. However, under the pessimal stable matching, players only obtain the least reward among all stable matchings. To maximize players' profits, player-optimal stable matching would be the most desirable. Though \citet{basu21beyond} successfully bring an upper bound for player-optimal stable regret, their result can be exponentially large if players' preference gap is small. Whether a polynomial guarantee for this regret exists is a significant but still open problem. In this work, we provide a new algorithm named explore-then-Gale-Shapley (ETGS) and show that the optimal stable regret of each player can be upper bounded by $O(K\log T/\Delta^2)$ where $K$ is the number of arms, $T$ is the horizon and $\Delta$ is the players' minimum preference gap among the first $N+1$-ranked arms. This result significantly improves previous works which either have a weaker player-pessimal stable matching objective or apply only to markets with special assumptions. When the preferences of participants satisfy some special conditions, our regret upper bound also matches the previously derived lower bound.
Online Influence Maximization under Decreasing Cascade Model
May 19, 2023


Abstract:We study online influence maximization (OIM) under a new model of decreasing cascade (DC). This model is a generalization of the independent cascade (IC) model by considering the common phenomenon of market saturation. In DC, the chance of an influence attempt being successful reduces with previous failures. The effect is neglected by previous OIM works under IC and linear threshold models. We propose the DC-UCB algorithm to solve this problem, which achieves a regret bound of the same order as the state-of-the-art works on the IC model. Extensive experiments on both synthetic and real datasets show the effectiveness of our algorithm.
Best-of-three-worlds Analysis for Linear Bandits with Follow-the-regularized-leader Algorithm
Mar 13, 2023Abstract:The linear bandit problem has been studied for many years in both stochastic and adversarial settings. Designing an algorithm that can optimize the environment without knowing the loss type attracts lots of interest. \citet{LeeLWZ021} propose an algorithm that actively detects the loss type and then switches between different algorithms specially designed for different settings. However, such an approach requires meticulous designs to perform well in all settings. Follow-the-regularized-leader (FTRL) is another popular algorithm type that can adapt to different environments. This algorithm is of simple design and the regret bounds are shown to be optimal in traditional multi-armed bandit problems compared with the detect-switch type algorithms. Designing an FTRL-type algorithm for linear bandits is an important question that has been open for a long time. In this paper, we prove that the FTRL-type algorithm with a negative entropy regularizer can achieve the best-of-three-world results for the linear bandit problem with the tacit cooperation between the choice of the learning rate and the specially designed self-bounding inequality.
Improved Regret Bounds for Linear Adversarial MDPs via Linear Optimization
Feb 14, 2023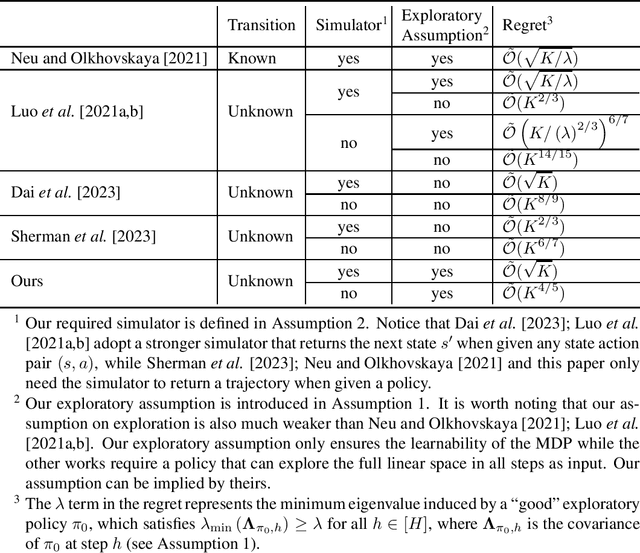
Abstract:Learning Markov decision processes (MDP) in an adversarial environment has been a challenging problem. The problem becomes even more challenging with function approximation, since the underlying structure of the loss function and transition kernel are especially hard to estimate in a varying environment. In fact, the state-of-the-art results for linear adversarial MDP achieve a regret of $\tilde{O}(K^{6/7})$ ($K$ denotes the number of episodes), which admits a large room for improvement. In this paper, we investigate the problem with a new view, which reduces linear MDP into linear optimization by subtly setting the feature maps of the bandit arms of linear optimization. This new technique, under an exploratory assumption, yields an improved bound of $\tilde{O}(K^{4/5})$ for linear adversarial MDP without access to a transition simulator. The new view could be of independent interest for solving other MDP problems that possess a linear structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge