Which LLM to Play? Convergence-Aware Online Model Selection with Time-Increasing Bandits
Paper and Code
Mar 11, 2024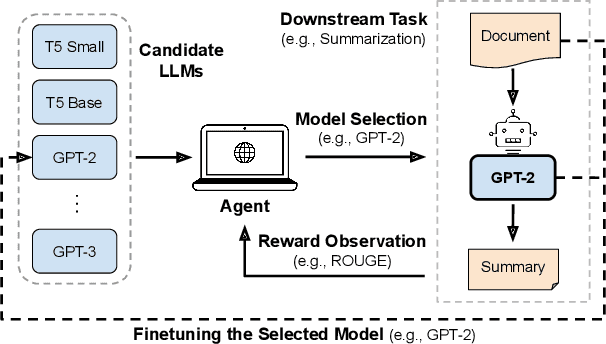
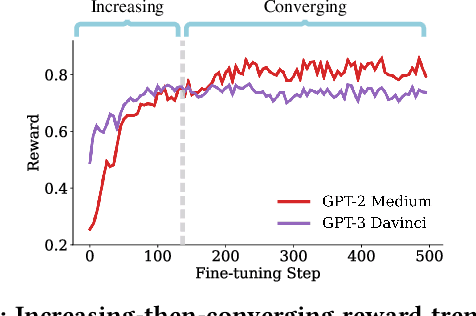
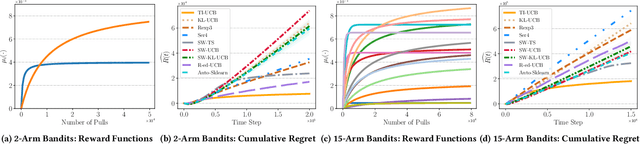
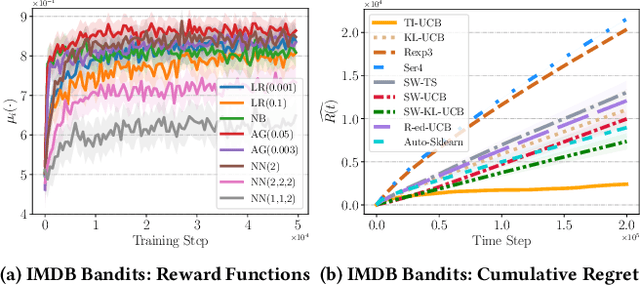
Web-based applications such as chatbots, search engines and news recommendations continue to grow in scale and complexity with the recent surge in the adoption of LLMs. Online model selection has thus garnered increasing attention due to the need to choose the best model among a diverse set while balancing task reward and exploration cost. Organizations faces decisions like whether to employ a costly API-based LLM or a locally finetuned small LLM, weighing cost against performance. Traditional selection methods often evaluate every candidate model before choosing one, which are becoming impractical given the rising costs of training and finetuning LLMs. Moreover, it is undesirable to allocate excessive resources towards exploring poor-performing models. While some recent works leverage online bandit algorithm to manage such exploration-exploitation trade-off in model selection, they tend to overlook the increasing-then-converging trend in model performances as the model is iteratively finetuned, leading to less accurate predictions and suboptimal model selections. In this paper, we propose a time-increasing bandit algorithm TI-UCB, which effectively predicts the increase of model performances due to finetuning and efficiently balances exploration and exploitation in model selection. To further capture the converging points of models, we develop a change detection mechanism by comparing consecutive increase predictions. We theoretically prove that our algorithm achieves a logarithmic regret upper bound in a typical increasing bandit setting, which implies a fast convergence rate. The advantage of our method is also empirically validated through extensive experiments on classification model selection and online selection of LLMs. Our results highlight the importance of utilizing increasing-then-converging pattern for more efficient and economic model selection in the deployment of LLMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge