Potential Score Matching: Debiasing Molecular Structure Sampling with Potential Energy Guidance

The ensemble average of physical properties of molecules is closely related to the distribution of molecular conformations, and sampling such distributions is a fundamental challenge in physics and chemistry. Traditional methods like molecular dynamics (MD) simulations and Markov chain Monte Carlo (MCMC) sampling are commonly used but can be time-consuming and costly. Recently, diffusion models have emerged as efficient alternatives by learning the distribution of training data. Obtaining an unbiased target distribution is still an expensive task, primarily because it requires satisfying ergodicity. To tackle these challenges, we propose Potential Score Matching (PSM), an approach that utilizes the potential energy gradient to guide generative models. PSM does not require exact energy functions and can debias sample distributions even when trained on limited and biased data. Our method outperforms existing state-of-the-art (SOTA) models on the Lennard-Jones (LJ) potential, a commonly used toy model. Furthermore, we extend the evaluation of PSM to high-dimensional problems using the MD17 and MD22 datasets. The results demonstrate that molecular distributions generated by PSM more closely approximate the Boltzmann distribution compared to traditional diffusion models.

Uni$\textbf{F}^2$ace: Fine-grained Face Understanding and Generation with Unified Multimodal Models

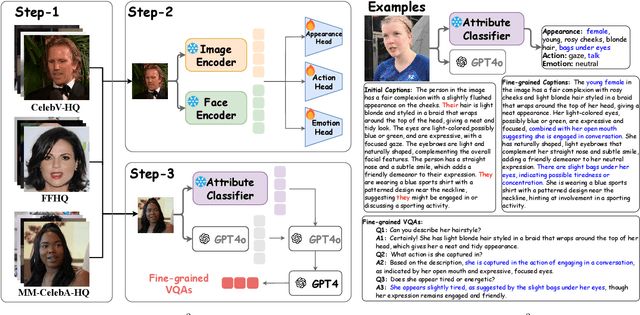
Unified multimodal models (UMMs) have emerged as a powerful paradigm in foundational computer vision research, demonstrating significant potential in both image understanding and generation. However, existing research in the face domain primarily focuses on $\textbf{coarse}$ facial attribute understanding, with limited capacity to handle $\textbf{fine-grained}$ facial attributes and without addressing generation capabilities. To overcome these limitations, we propose Uni$\textbf{F}^2$ace, the first UMM tailored specifically for fine-grained face understanding and generation. In general, we train Uni$\textbf{F}^2$ace on a self-constructed, specialized dataset utilizing two mutually beneficial diffusion techniques and a two-level mixture-of-experts architecture. Specifically, we first build a large-scale facial dataset, Uni$\textbf{F}^2$ace-130K, which contains 130K image-text pairs with one million question-answering pairs that span a wide range of facial attributes. Second, we establish a theoretical connection between discrete diffusion score matching and masked generative models, optimizing both evidence lower bounds simultaneously, which significantly improves the model's ability to synthesize facial details. Finally, we introduce both token-level and sequence-level mixture-of-experts, enabling efficient fine-grained representation learning for both understanding and generation tasks. Extensive experiments on Uni$\textbf{F}^2$ace-130K demonstrate that Uni$\textbf{F}^2$ace outperforms existing UMMs and generative models, achieving superior performance across both understanding and generation tasks.

UniGenX: Unified Generation of Sequence and Structure with Autoregressive Diffusion

Unified generation of sequence and structure for scientific data (e.g., materials, molecules, proteins) is a critical task. Existing approaches primarily rely on either autoregressive sequence models or diffusion models, each offering distinct advantages and facing notable limitations. Autoregressive models, such as GPT, Llama, and Phi-4, have demonstrated remarkable success in natural language generation and have been extended to multimodal tasks (e.g., image, video, and audio) using advanced encoders like VQ-VAE to represent complex modalities as discrete sequences. However, their direct application to scientific domains is challenging due to the high precision requirements and the diverse nature of scientific data. On the other hand, diffusion models excel at generating high-dimensional scientific data, such as protein, molecule, and material structures, with remarkable accuracy. Yet, their inability to effectively model sequences limits their potential as general-purpose multimodal foundation models. To address these challenges, we propose UniGenX, a unified framework that combines autoregressive next-token prediction with conditional diffusion models. This integration leverages the strengths of autoregressive models to ease the training of conditional diffusion models, while diffusion-based generative heads enhance the precision of autoregressive predictions. We validate the effectiveness of UniGenX on material and small molecule generation tasks, achieving a significant leap in state-of-the-art performance for material crystal structure prediction and establishing new state-of-the-art results for small molecule structure prediction, de novo design, and conditional generation. Notably, UniGenX demonstrates significant improvements, especially in handling long sequences for complex structures, showcasing its efficacy as a versatile tool for scientific data generation.

Weak Collocation Regression for Inferring Stochastic Dynamics with Lévy Noise

With the rapid increase of observational, experimental and simulated data for stochastic systems, tremendous efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the broad applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extracting stochastic dynamics with L\'{e}vy noise are relatively few. In this work, we propose a Weak Collocation Regression (WCR) to explicitly reveal unknown stochastic dynamical systems, i.e., the Stochastic Differential Equation (SDE) with both $\alpha$-stable L\'{e}vy noise and Gaussian noise, from discrete aggregate data. This method utilizes the evolution equation of the probability distribution function, i.e., the Fokker-Planck (FP) equation. With the weak form of the FP equation, the WCR constructs a linear system of unknown parameters where all integrals are evaluated by Monte Carlo method with the observations. Then, the unknown parameters are obtained by a sparse linear regression. For a SDE with L\'{e}vy noise, the corresponding FP equation is a partial integro-differential equation (PIDE), which contains nonlocal terms, and is difficult to deal with. The weak form can avoid complicated multiple integrals. Our approach can simultaneously distinguish mixed noise types, even in multi-dimensional problems. Numerical experiments demonstrate that our method is accurate and computationally efficient.

Which LLM to Play? Convergence-Aware Online Model Selection with Time-Increasing Bandits

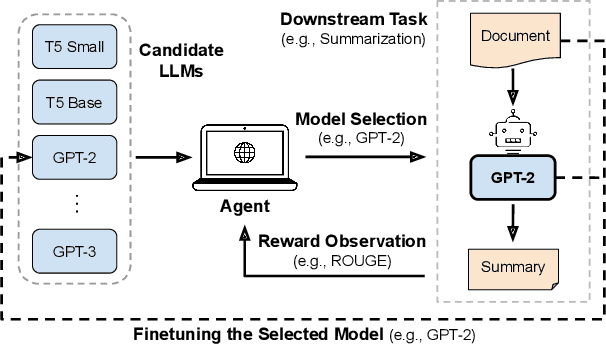
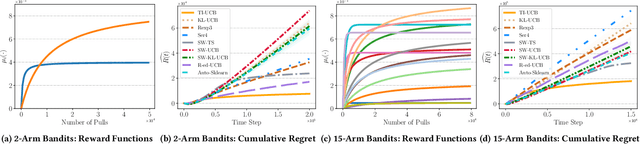
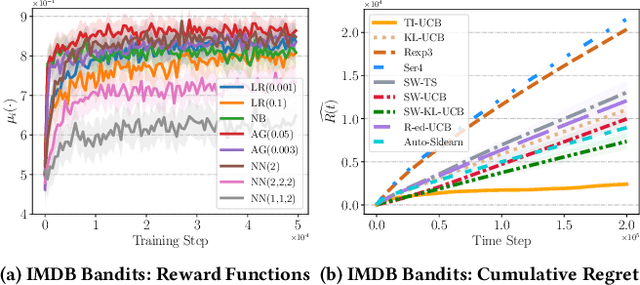
Web-based applications such as chatbots, search engines and news recommendations continue to grow in scale and complexity with the recent surge in the adoption of LLMs. Online model selection has thus garnered increasing attention due to the need to choose the best model among a diverse set while balancing task reward and exploration cost. Organizations faces decisions like whether to employ a costly API-based LLM or a locally finetuned small LLM, weighing cost against performance. Traditional selection methods often evaluate every candidate model before choosing one, which are becoming impractical given the rising costs of training and finetuning LLMs. Moreover, it is undesirable to allocate excessive resources towards exploring poor-performing models. While some recent works leverage online bandit algorithm to manage such exploration-exploitation trade-off in model selection, they tend to overlook the increasing-then-converging trend in model performances as the model is iteratively finetuned, leading to less accurate predictions and suboptimal model selections. In this paper, we propose a time-increasing bandit algorithm TI-UCB, which effectively predicts the increase of model performances due to finetuning and efficiently balances exploration and exploitation in model selection. To further capture the converging points of models, we develop a change detection mechanism by comparing consecutive increase predictions. We theoretically prove that our algorithm achieves a logarithmic regret upper bound in a typical increasing bandit setting, which implies a fast convergence rate. The advantage of our method is also empirically validated through extensive experiments on classification model selection and online selection of LLMs. Our results highlight the importance of utilizing increasing-then-converging pattern for more efficient and economic model selection in the deployment of LLMs.