Weak Collocation Regression for Inferring Stochastic Dynamics with Lévy Noise

With the rapid increase of observational, experimental and simulated data for stochastic systems, tremendous efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the broad applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extracting stochastic dynamics with L\'{e}vy noise are relatively few. In this work, we propose a Weak Collocation Regression (WCR) to explicitly reveal unknown stochastic dynamical systems, i.e., the Stochastic Differential Equation (SDE) with both $\alpha$-stable L\'{e}vy noise and Gaussian noise, from discrete aggregate data. This method utilizes the evolution equation of the probability distribution function, i.e., the Fokker-Planck (FP) equation. With the weak form of the FP equation, the WCR constructs a linear system of unknown parameters where all integrals are evaluated by Monte Carlo method with the observations. Then, the unknown parameters are obtained by a sparse linear regression. For a SDE with L\'{e}vy noise, the corresponding FP equation is a partial integro-differential equation (PIDE), which contains nonlocal terms, and is difficult to deal with. The weak form can avoid complicated multiple integrals. Our approach can simultaneously distinguish mixed noise types, even in multi-dimensional problems. Numerical experiments demonstrate that our method is accurate and computationally efficient.

A note on the adjoint method for neural ordinary differential equation network

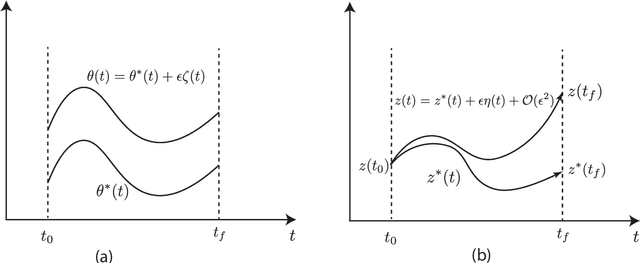
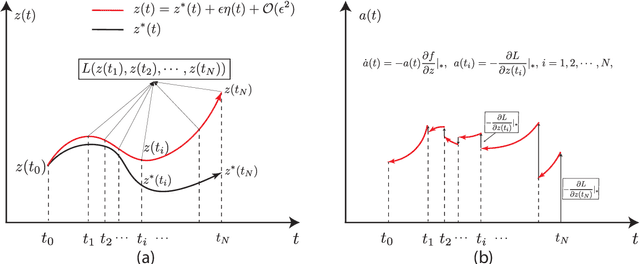
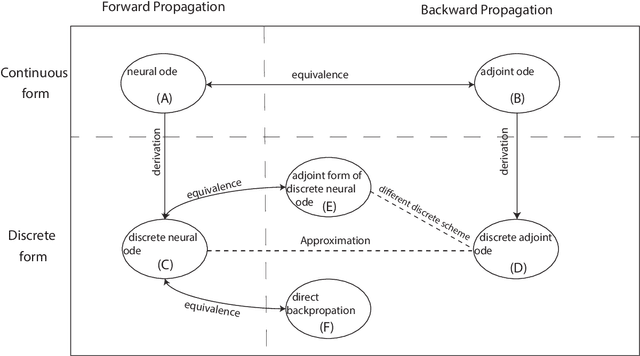
Perturbation and operator adjoint method are used to give the right adjoint form rigourously. From the derivation, we can have following results: 1) The loss gradient is not an ODE, it is an integral and we shows the reason; 2) The traditional adjoint form is not equivalent with the back propagation results. 3) The adjoint operator analysis shows that if and only if the discrete adjoint has the same scheme with the discrete neural ODE, the adjoint form would give the same results as BP does.

Reconstruction of dynamical systems from data without time labels

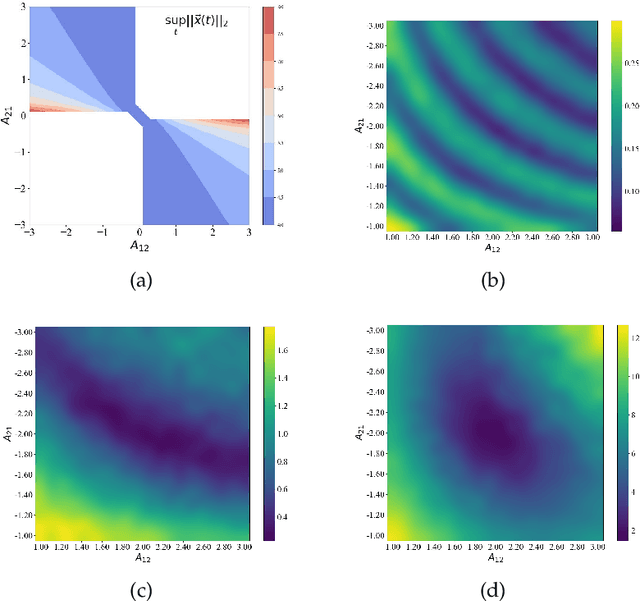
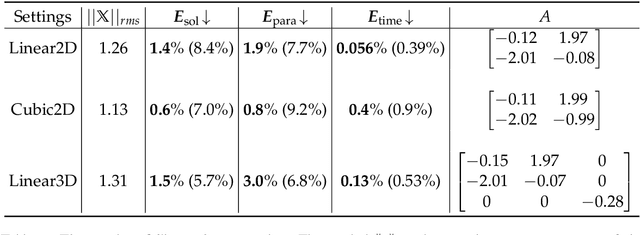
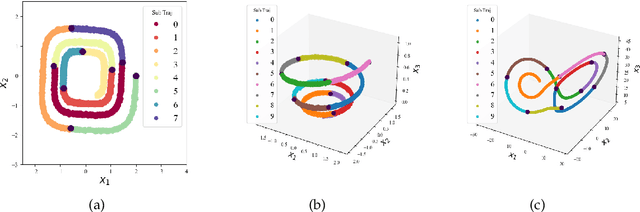
In this paper, we study the method to reconstruct dynamical systems from data without time labels. Data without time labels appear in many applications, such as molecular dynamics, single-cell RNA sequencing etc. Reconstruction of dynamical system from time sequence data has been studied extensively. However, these methods do not apply if time labels are unknown. Without time labels, sequence data becomes distribution data. Based on this observation, we propose to treat the data as samples from a probability distribution and try to reconstruct the underlying dynamical system by minimizing the distribution loss, sliced Wasserstein distance more specifically. Extensive experiment results demonstrate the effectiveness of the proposed method.

DCM: Deep complementary energy method based on the principle of minimum complementary energy

The principle of minimum potential and complementary energy are the most important variational principles in solid mechanics. The deep energy method (DEM), which has received much attention, is based on the principle of minimum potential energy, but it lacks the important form of minimum complementary energy. To fill the gap, we propose a deep complementary energy method (DCM) based on the principle of minimum complementary energy. The output function of DCM is the stress function that naturally satisfies the equilibrium equation. We extend the proposed DCM algorithm to DCM-Plus (DCM-P), adding the terms that naturally satisfy the biharmonic equation in the Airy stress function. We combine operator learning with physical equations and propose a deep complementary energy operator method (DCM-O), including branch net, trunk net, basis net, and particular net. DCM-O first combines existing high-fidelity numerical results to train DCM-O through data. Then the complementary energy is used to train the branch net and trunk net in DCM-O. To analyze DCM performance, we present the numerical result of the most common stress functions, the Prandtl and Airy stress function. The proposed method DCM is used to model the representative mechanical problems with different types of boundary conditions. We compare DCM with the existing PINNs and DEM algorithms. The result shows the advantage of the proposed DCM is suitable for dealing with problems of dominated displacement boundary conditions, which is proved by mathematical derivations, as well as with numerical experiments. DCM-P and DCM-O can improve the accuracy and efficiency of DCM. DCM is an essential supplementary energy form to the deep energy method. Operator learning based on the energy method can balance data and physical equations well, giving computational mechanics broad research prospects.

Weak Collocation Regression method: fast reveal hidden stochastic dynamics from high-dimensional aggregate data

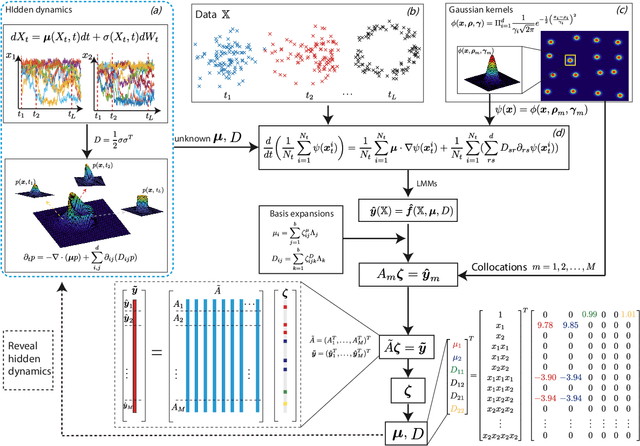
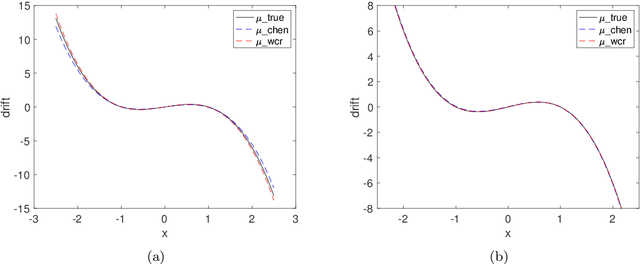
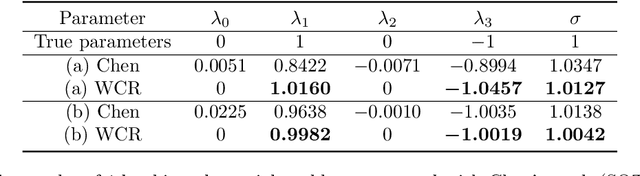
Revealing hidden dynamics from the stochastic data is a challenging problem as randomness takes part in the evolution of the data. The problem becomes exceedingly complex when the trajectories of the stochastic data are absent in many scenarios. Here we present an approach to effectively modeling the dynamics of the stochastic data without trajectories based on the weak form of the Fokker-Planck (FP) equation, which governs the evolution of the density function in the Brownian process. Taking the collocations of Gaussian functions as the test functions in the weak form of the FP equation, we transfer the derivatives to the Gaussian functions and thus approximate the weak form by the expectational sum of the data. With a dictionary representation of the unknown terms, a linear system is built and then solved by the regression, revealing the unknown dynamics of the data. Hence, we name the method with the Weak Collocation Regression (WCR) method for its three key components: weak form, collocation of Gaussian kernels, and regression. The numerical experiments show that our method is flexible and fast, which reveals the dynamics within seconds in multi-dimensional problems and can be easily extended to high-dimensional data such as 20 dimensions. WCR can also correctly identify the hidden dynamics of the complex tasks with variable-dependent diffusion and coupled drift, and the performance is robust, achieving high accuracy in the case with noise added.

BI-GreenNet: Learning Green's functions by boundary integral network

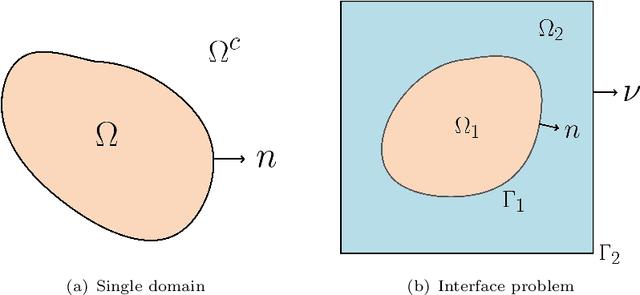
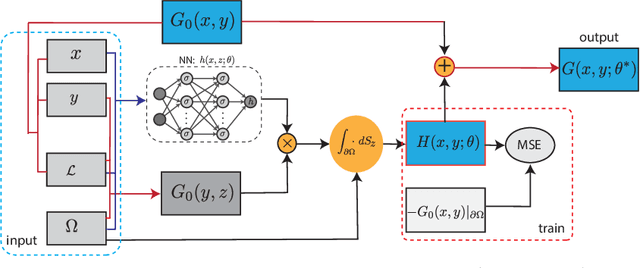
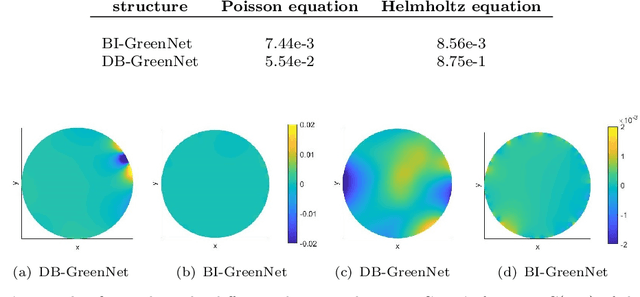
Green's function plays a significant role in both theoretical analysis and numerical computing of partial differential equations (PDEs). However, in most cases, Green's function is difficult to compute. The troubles arise in the following three folds. Firstly, compared with the original PDE, the dimension of Green's function is doubled, making it impossible to be handled by traditional mesh-based methods. Secondly, Green's function usually contains singularities which increase the difficulty to get a good approximation. Lastly, the computational domain may be very complex or even unbounded. To override these problems, we leverage the fundamental solution, boundary integral method and neural networks to develop a new method for computing Green's function with high accuracy in this paper. We focus on Green's function of Poisson and Helmholtz equations in bounded domains, unbounded domains. We also consider Poisson equation and Helmholtz domains with interfaces. Extensive numerical experiments illustrate the efficiency and the accuracy of our method for solving Green's function. In addition, we also use the Green's function calculated by our method to solve a class of PDE, and also obtain high-precision solutions, which shows the good generalization ability of our method on solving PDEs.

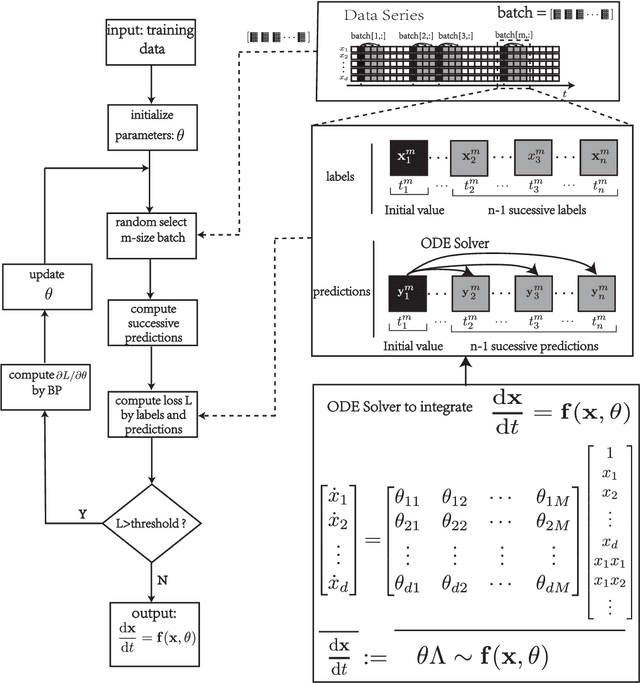
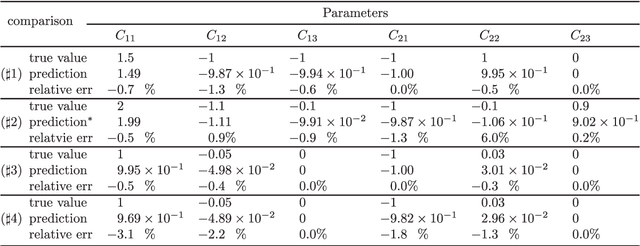
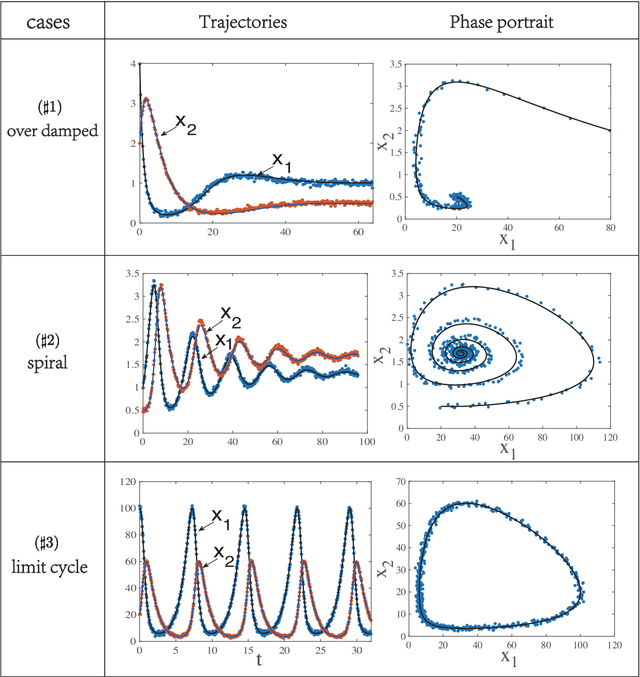
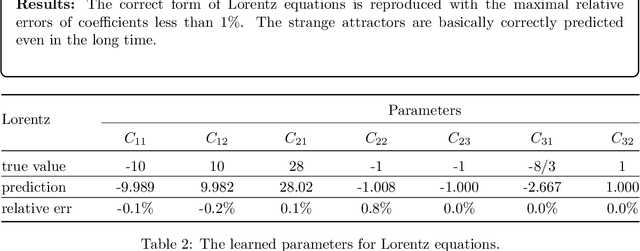
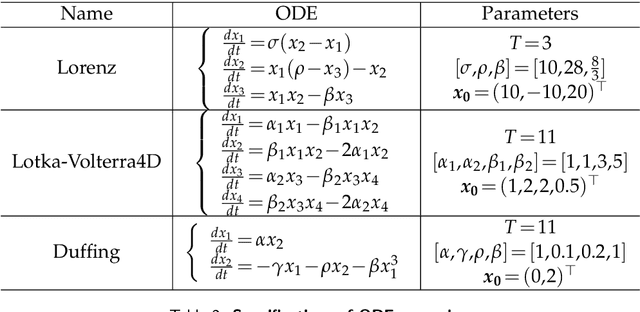
Revealing hidden dynamics from time-series data by ODENet

To understand the hidden physical concepts from observed data is the most basic but challenging problem in many fields. In this study, we propose a new type of interpretable neural network called the ordinary differential equation network (ODENet) to reveal the hidden dynamics buried in the massive time-series data. Specifically, we construct explicit models presented by ordinary differential equations (ODEs) to describe the observed data without any prior knowledge. In contrast to other previous neural networks which are black boxes for users, the ODENet in this work is an imitation of the difference scheme for ODEs, with each step computed by an ODE solver, and thus is completely understandable. Backpropagation algorithms are used to update the coefficients of a group of orthogonal basis functions, which specify the concrete form of ODEs, under the guidance of loss function with sparsity requirement. From classical Lotka-Volterra equations to chaotic Lorenz equations, the ODENet demonstrates its remarkable capability to deal with time-series data. In the end, we apply the ODENet to real actin aggregation data observed by experimentalists, and it shows an impressive performance as well.