Weak Collocation Regression for Inferring Stochastic Dynamics with Lévy Noise

With the rapid increase of observational, experimental and simulated data for stochastic systems, tremendous efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the broad applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extracting stochastic dynamics with L\'{e}vy noise are relatively few. In this work, we propose a Weak Collocation Regression (WCR) to explicitly reveal unknown stochastic dynamical systems, i.e., the Stochastic Differential Equation (SDE) with both $\alpha$-stable L\'{e}vy noise and Gaussian noise, from discrete aggregate data. This method utilizes the evolution equation of the probability distribution function, i.e., the Fokker-Planck (FP) equation. With the weak form of the FP equation, the WCR constructs a linear system of unknown parameters where all integrals are evaluated by Monte Carlo method with the observations. Then, the unknown parameters are obtained by a sparse linear regression. For a SDE with L\'{e}vy noise, the corresponding FP equation is a partial integro-differential equation (PIDE), which contains nonlocal terms, and is difficult to deal with. The weak form can avoid complicated multiple integrals. Our approach can simultaneously distinguish mixed noise types, even in multi-dimensional problems. Numerical experiments demonstrate that our method is accurate and computationally efficient.

Neural Born Series Operator for Biomedical Ultrasound Computed Tomography

Ultrasound Computed Tomography (USCT) provides a radiation-free option for high-resolution clinical imaging. Despite its potential, the computationally intensive Full Waveform Inversion (FWI) required for tissue property reconstruction limits its clinical utility. This paper introduces the Neural Born Series Operator (NBSO), a novel technique designed to speed up wave simulations, thereby facilitating a more efficient USCT image reconstruction process through an NBSO-based FWI pipeline. Thoroughly validated on comprehensive brain and breast datasets, simulated under experimental USCT conditions, the NBSO proves to be accurate and efficient in both forward simulation and image reconstruction. This advancement demonstrates the potential of neural operators in facilitating near real-time USCT reconstruction, making the clinical application of USCT increasingly viable and promising.

Reconstruction of dynamical systems from data without time labels

In this paper, we study the method to reconstruct dynamical systems from data without time labels. Data without time labels appear in many applications, such as molecular dynamics, single-cell RNA sequencing etc. Reconstruction of dynamical system from time sequence data has been studied extensively. However, these methods do not apply if time labels are unknown. Without time labels, sequence data becomes distribution data. Based on this observation, we propose to treat the data as samples from a probability distribution and try to reconstruct the underlying dynamical system by minimizing the distribution loss, sliced Wasserstein distance more specifically. Extensive experiment results demonstrate the effectiveness of the proposed method.

Weak Collocation Regression method: fast reveal hidden stochastic dynamics from high-dimensional aggregate data

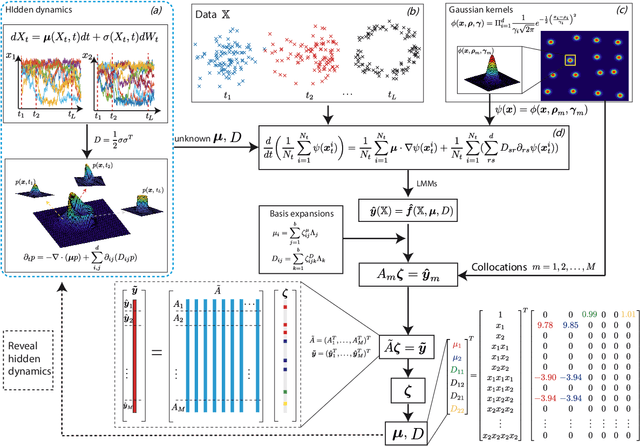
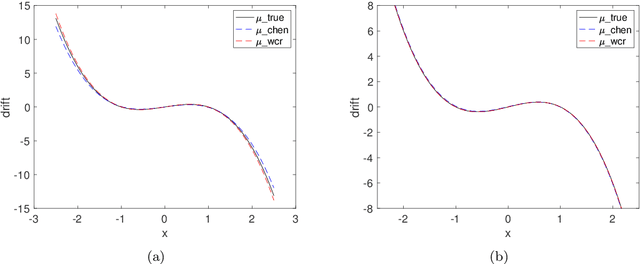
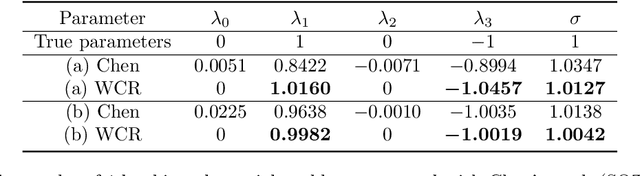
Revealing hidden dynamics from the stochastic data is a challenging problem as randomness takes part in the evolution of the data. The problem becomes exceedingly complex when the trajectories of the stochastic data are absent in many scenarios. Here we present an approach to effectively modeling the dynamics of the stochastic data without trajectories based on the weak form of the Fokker-Planck (FP) equation, which governs the evolution of the density function in the Brownian process. Taking the collocations of Gaussian functions as the test functions in the weak form of the FP equation, we transfer the derivatives to the Gaussian functions and thus approximate the weak form by the expectational sum of the data. With a dictionary representation of the unknown terms, a linear system is built and then solved by the regression, revealing the unknown dynamics of the data. Hence, we name the method with the Weak Collocation Regression (WCR) method for its three key components: weak form, collocation of Gaussian kernels, and regression. The numerical experiments show that our method is flexible and fast, which reveals the dynamics within seconds in multi-dimensional problems and can be easily extended to high-dimensional data such as 20 dimensions. WCR can also correctly identify the hidden dynamics of the complex tasks with variable-dependent diffusion and coupled drift, and the performance is robust, achieving high accuracy in the case with noise added.

A Deep Learning Approach to Predicting Ventilator Parameters for Mechanically Ventilated Septic Patients

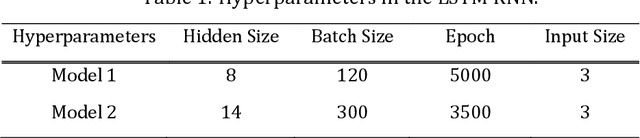
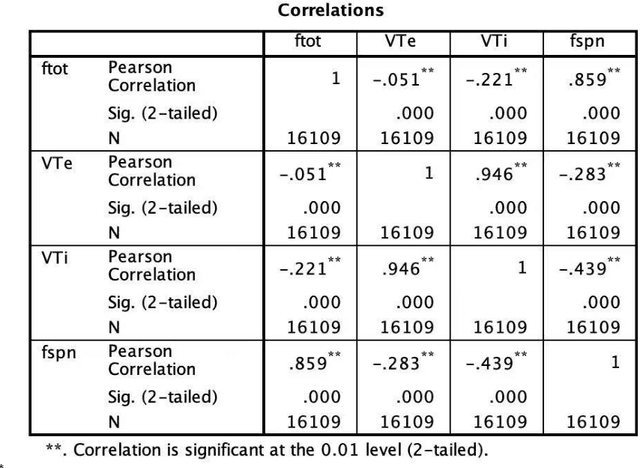
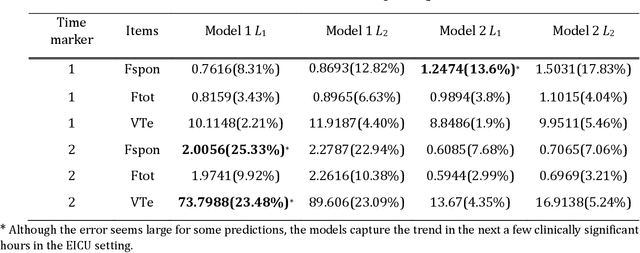
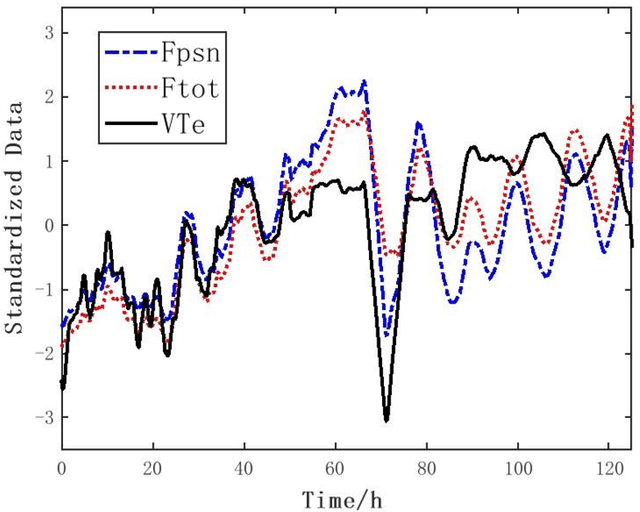
We develop a deep learning approach to predicting a set of ventilator parameters for a mechanically ventilated septic patient using a long and short term memory (LSTM) recurrent neural network (RNN) model. We focus on short-term predictions of a set of ventilator parameters for the septic patient in emergency intensive care unit (EICU). The short-term predictability of the model provides attending physicians with early warnings to make timely adjustment to the treatment of the patient in the EICU. The patient specific deep learning model can be trained on any given critically ill patient, making it an intelligent aide for physicians to use in emergent medical situations.