A Regularized Newton Method for Nonconvex Optimization with Global and Local Complexity Guarantees

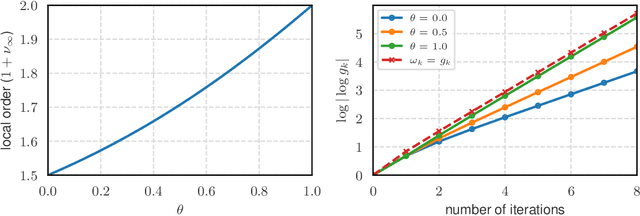
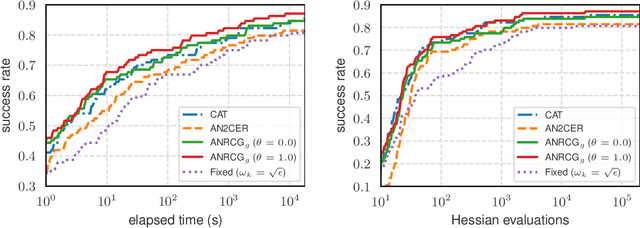
We consider the problem of finding an $\epsilon$-stationary point of a nonconvex function with a Lipschitz continuous Hessian and propose a quadratic regularized Newton method incorporating a new class of regularizers constructed from the current and previous gradients. The method leverages a recently developed linear conjugate gradient approach with a negative curvature monitor to solve the regularized Newton equation. Notably, our algorithm is adaptive, requiring no prior knowledge of the Lipschitz constant of the Hessian, and achieves a global complexity of $O(\epsilon^{-\frac{3}{2}}) + \tilde O(1)$ in terms of the second-order oracle calls, and $\tilde O(\epsilon^{-\frac{7}{4}})$ for Hessian-vector products, respectively. Moreover, when the iterates converge to a point where the Hessian is positive definite, the method exhibits quadratic local convergence. Preliminary numerical results illustrate the competitiveness of our algorithm.

Fast and Scalable Semi-Supervised Learning for Multi-View Subspace Clustering

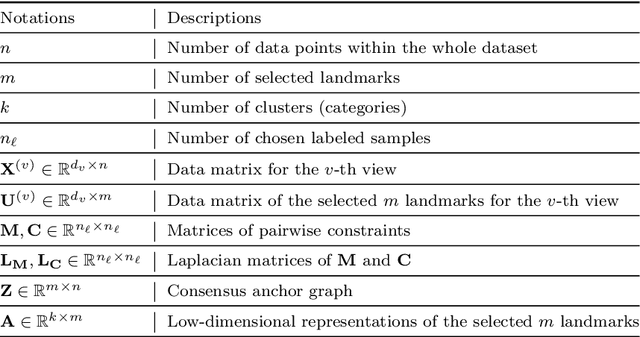
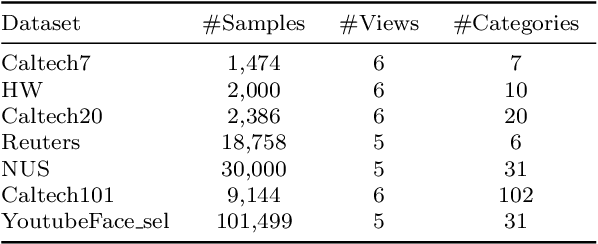
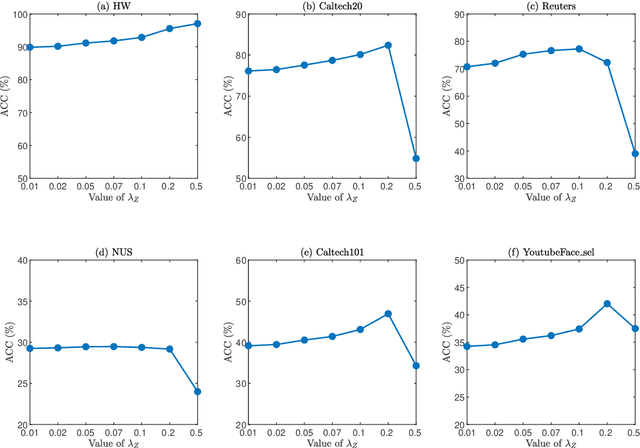
In this paper, we introduce a Fast and Scalable Semi-supervised Multi-view Subspace Clustering (FSSMSC) method, a novel solution to the high computational complexity commonly found in existing approaches. FSSMSC features linear computational and space complexity relative to the size of the data. The method generates a consensus anchor graph across all views, representing each data point as a sparse linear combination of chosen landmarks. Unlike traditional methods that manage the anchor graph construction and the label propagation process separately, this paper proposes a unified optimization model that facilitates simultaneous learning of both. An effective alternating update algorithm with convergence guarantees is proposed to solve the unified optimization model. Additionally, the method employs the obtained anchor graph and landmarks' low-dimensional representations to deduce low-dimensional representations for raw data. Following this, a straightforward clustering approach is conducted on these low-dimensional representations to achieve the final clustering results. The effectiveness and efficiency of FSSMSC are validated through extensive experiments on multiple benchmark datasets of varying scales.

Interface Laplace Learning: Learnable Interface Term Helps Semi-Supervised Learning

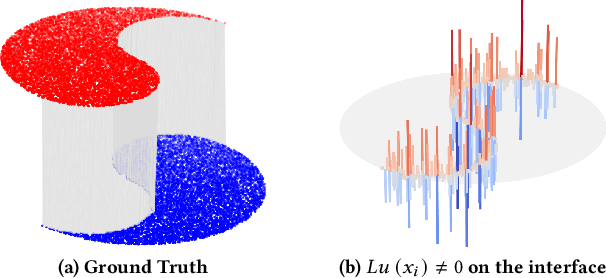
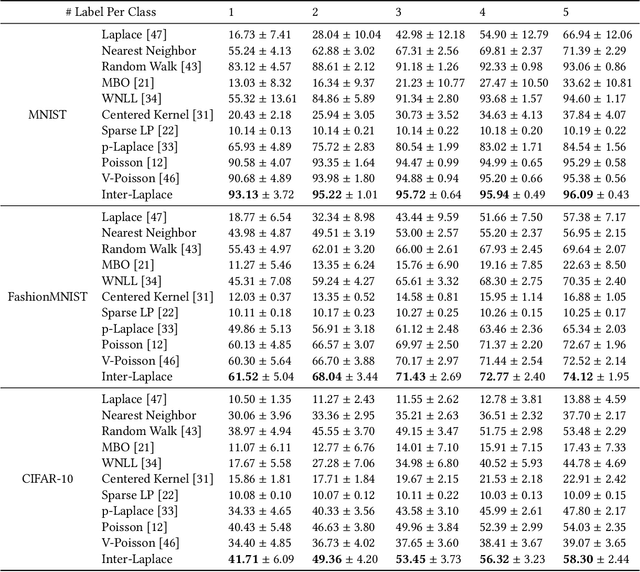
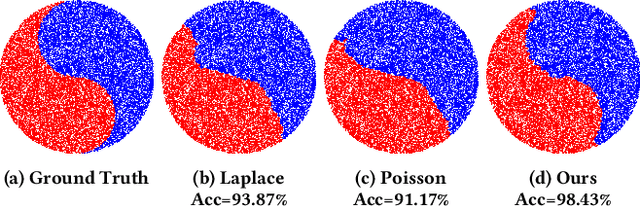
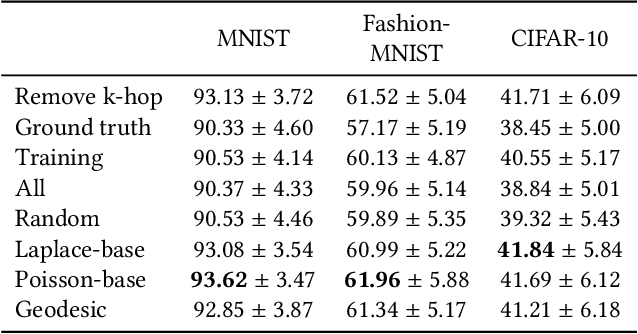
We introduce a novel framework, called Interface Laplace learning, for graph-based semi-supervised learning. Motivated by the observation that an interface should exist between different classes where the function value is non-smooth, we introduce a Laplace learning model that incorporates an interface term. This model challenges the long-standing assumption that functions are smooth at all unlabeled points. In the proposed approach, we add an interface term to the Laplace learning model at the interface positions. We provide a practical algorithm to approximate the interface positions using k-hop neighborhood indices, and to learn the interface term from labeled data without artificial design. Our method is efficient and effective, and we present extensive experiments demonstrating that Interface Laplace learning achieves better performance than other recent semi-supervised learning approaches at extremely low label rates on the MNIST, FashionMNIST, and CIFAR-10 datasets.

SeNM-VAE: Semi-Supervised Noise Modeling with Hierarchical Variational Autoencoder

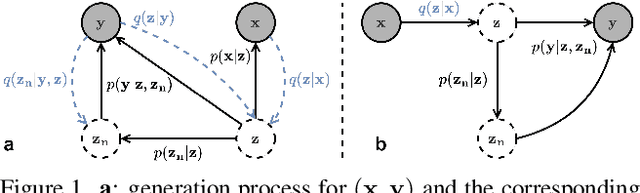
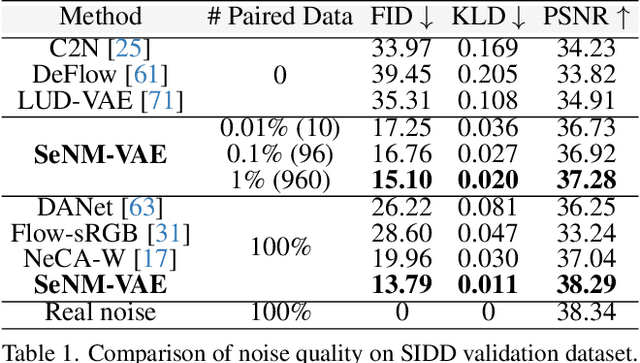
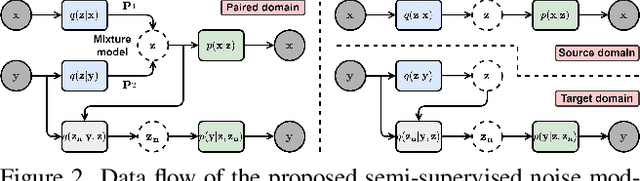
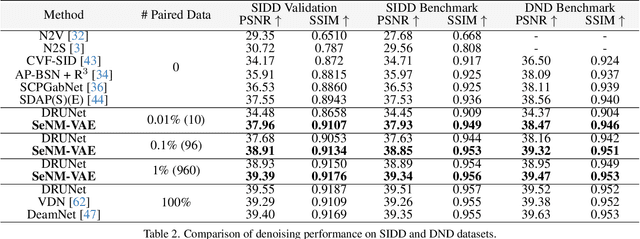
The data bottleneck has emerged as a fundamental challenge in learning based image restoration methods. Researchers have attempted to generate synthesized training data using paired or unpaired samples to address this challenge. This study proposes SeNM-VAE, a semi-supervised noise modeling method that leverages both paired and unpaired datasets to generate realistic degraded data. Our approach is based on modeling the conditional distribution of degraded and clean images with a specially designed graphical model. Under the variational inference framework, we develop an objective function for handling both paired and unpaired data. We employ our method to generate paired training samples for real-world image denoising and super-resolution tasks. Our approach excels in the quality of synthetic degraded images compared to other unpaired and paired noise modeling methods. Furthermore, our approach demonstrates remarkable performance in downstream image restoration tasks, even with limited paired data. With more paired data, our method achieves the best performance on the SIDD dataset.

Convection-Diffusion Equation: A Theoretically Certified Framework for Neural Networks

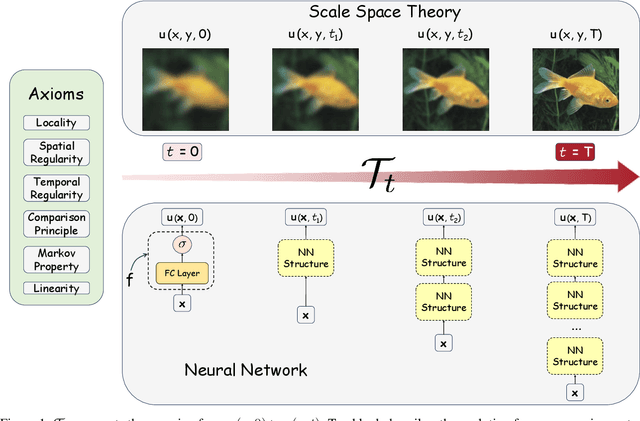
In this paper, we study the partial differential equation models of neural networks. Neural network can be viewed as a map from a simple base model to a complicate function. Based on solid analysis, we show that this map can be formulated by a convection-diffusion equation. This theoretically certified framework gives mathematical foundation and more understanding of neural networks. Moreover, based on the convection-diffusion equation model, we design a novel network structure, which incorporates diffusion mechanism into network architecture. Extensive experiments on both benchmark datasets and real-world applications validate the performance of the proposed model.

Reconstruction of dynamical systems from data without time labels

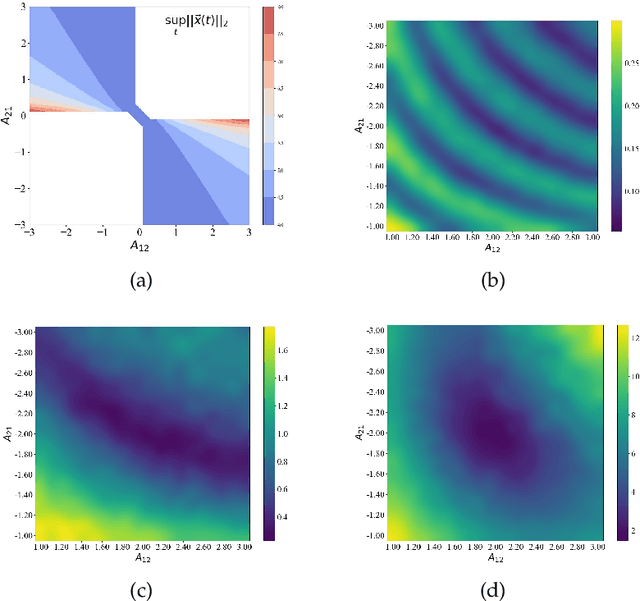
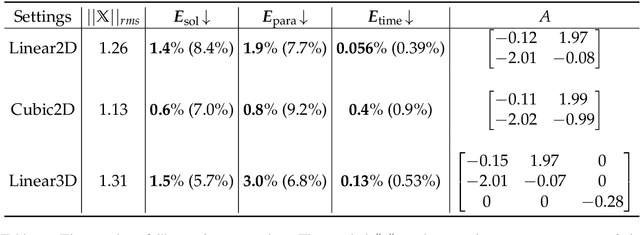
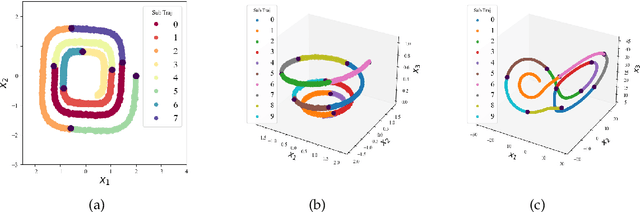
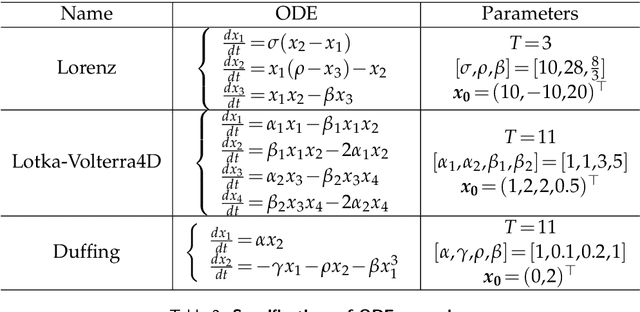
In this paper, we study the method to reconstruct dynamical systems from data without time labels. Data without time labels appear in many applications, such as molecular dynamics, single-cell RNA sequencing etc. Reconstruction of dynamical system from time sequence data has been studied extensively. However, these methods do not apply if time labels are unknown. Without time labels, sequence data becomes distribution data. Based on this observation, we propose to treat the data as samples from a probability distribution and try to reconstruct the underlying dynamical system by minimizing the distribution loss, sliced Wasserstein distance more specifically. Extensive experiment results demonstrate the effectiveness of the proposed method.

Addressing preferred orientation in single-particle cryo-EM through AI-generated auxiliary particles

The single-particle cryo-EM field faces the persistent challenge of preferred orientation, lacking general computational solutions. We introduce cryoPROS, an AI-based approach designed to address the above issue. By generating the auxiliary particles with a conditional deep generative model, cryoPROS addresses the intrinsic bias in orientation estimation for the observed particles. We effectively employed cryoPROS in the cryo-EM single particle analysis of the hemagglutinin trimer, showing the ability to restore the near-atomic resolution structure on non-tilt data. Moreover, the enhanced version named cryoPROS-MP significantly improves the resolution of the membrane protein NaX using the no-tilted data that contains the effects of micelles. Compared to the classical approaches, cryoPROS does not need special experimental or image acquisition techniques, providing a purely computational yet effective solution for the preferred orientation problem. Finally, we conduct extensive experiments that establish the low risk of model bias and the high robustness of cryoPROS.

An axiomatized PDE model of deep neural networks

Inspired by the relation between deep neural network (DNN) and partial differential equations (PDEs), we study the general form of the PDE models of deep neural networks. To achieve this goal, we formulate DNN as an evolution operator from a simple base model. Based on several reasonable assumptions, we prove that the evolution operator is actually determined by convection-diffusion equation. This convection-diffusion equation model gives mathematical explanation for several effective networks. Moreover, we show that the convection-diffusion model improves the robustness and reduces the Rademacher complexity. Based on the convection-diffusion equation, we design a new training method for ResNets. Experiments validate the performance of the proposed method.

Semi-Supervised Clustering via Dynamic Graph Structure Learning

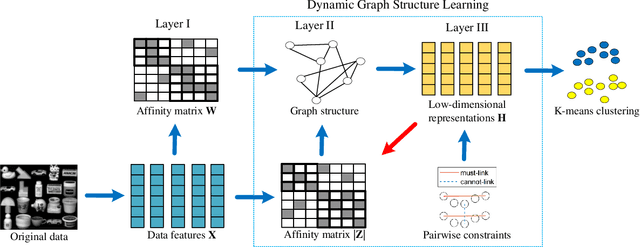
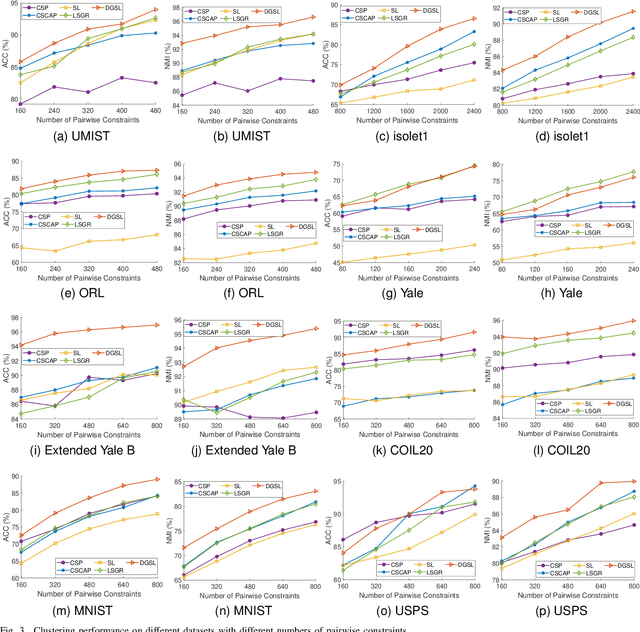
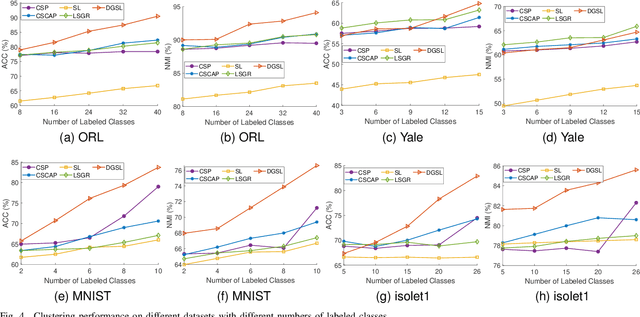
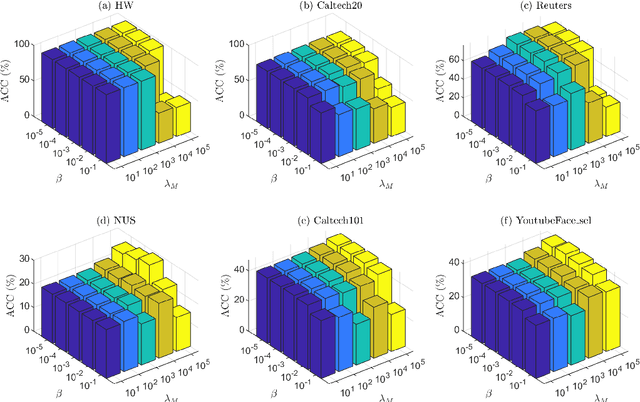
Most existing semi-supervised graph-based clustering methods exploit the supervisory information by either refining the affinity matrix or directly constraining the low-dimensional representations of data points. The affinity matrix represents the graph structure and is vital to the performance of semi-supervised graph-based clustering. However, existing methods adopt a static affinity matrix to learn the low-dimensional representations of data points and do not optimize the affinity matrix during the learning process. In this paper, we propose a novel dynamic graph structure learning method for semi-supervised clustering. In this method, we simultaneously optimize the affinity matrix and the low-dimensional representations of data points by leveraging the given pairwise constraints. Moreover, we propose an alternating minimization approach with proven convergence to solve the proposed nonconvex model. During the iteration process, our method cyclically updates the low-dimensional representations of data points and refines the affinity matrix, leading to a dynamic affinity matrix (graph structure). Specifically, for the update of the affinity matrix, we enforce the data points with remarkably different low-dimensional representations to have an affinity value of 0. Furthermore, we construct the initial affinity matrix by integrating the local distance and global self-representation among data points. Experimental results on eight benchmark datasets under different settings show the advantages of the proposed approach.

Convergence Rates of Training Deep Neural Networks via Alternating Minimization Methods

Training deep neural networks (DNNs) is an important and challenging optimization problem in machine learning due to its non-convexity and non-separable structure. The alternating minimization (AM) approaches split the composition structure of DNNs and have drawn great interest in the deep learning and optimization communities. In this paper, we propose a unified framework for analyzing the convergence rate of AM-type network training methods. Our analysis are based on the $j$-step sufficient decrease conditions and the Kurdyka-Lojasiewicz (KL) property, which relaxes the requirement of designing descent algorithms. We show the detailed local convergence rate if the KL exponent $\theta$ varies in $[0,1)$. Moreover, the local R-linear convergence is discussed under a stronger $j$-step sufficient decrease condition.