Interface Laplace Learning: Learnable Interface Term Helps Semi-Supervised Learning

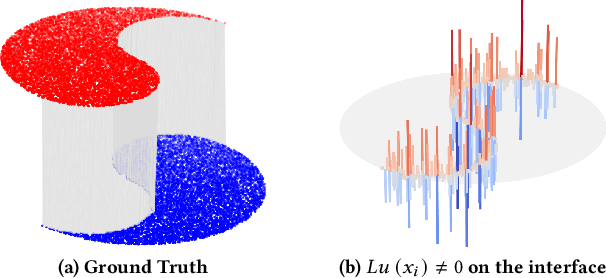
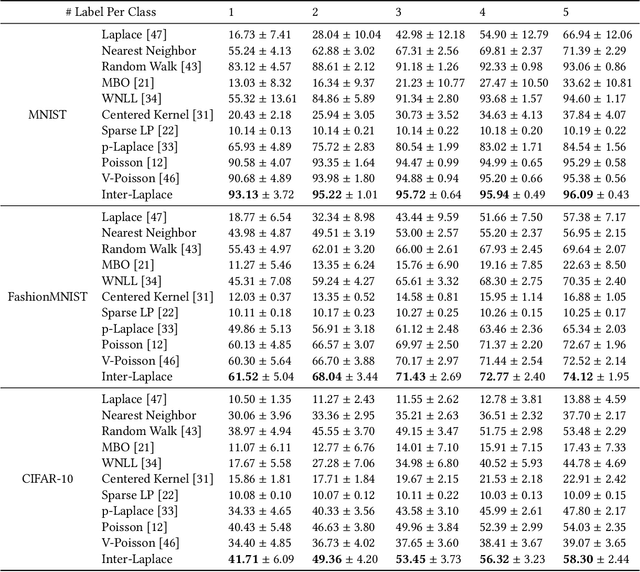
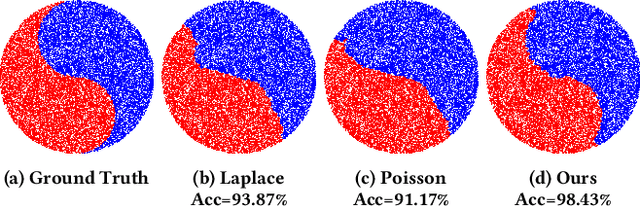
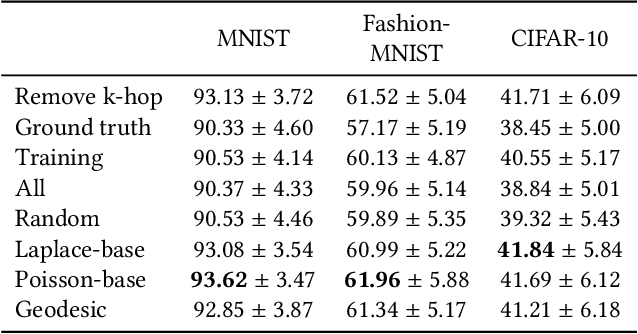
We introduce a novel framework, called Interface Laplace learning, for graph-based semi-supervised learning. Motivated by the observation that an interface should exist between different classes where the function value is non-smooth, we introduce a Laplace learning model that incorporates an interface term. This model challenges the long-standing assumption that functions are smooth at all unlabeled points. In the proposed approach, we add an interface term to the Laplace learning model at the interface positions. We provide a practical algorithm to approximate the interface positions using k-hop neighborhood indices, and to learn the interface term from labeled data without artificial design. Our method is efficient and effective, and we present extensive experiments demonstrating that Interface Laplace learning achieves better performance than other recent semi-supervised learning approaches at extremely low label rates on the MNIST, FashionMNIST, and CIFAR-10 datasets.

Convection-Diffusion Equation: A Theoretically Certified Framework for Neural Networks

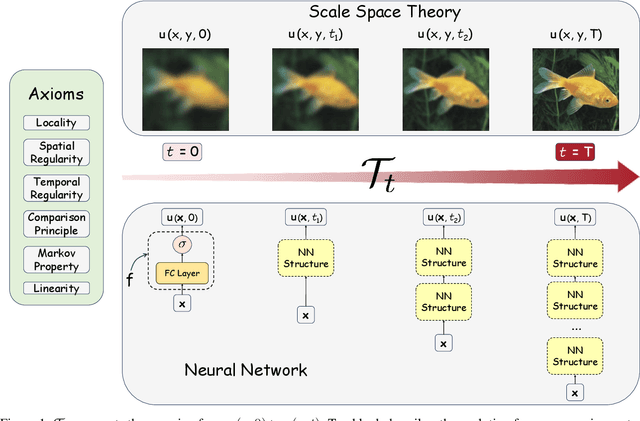
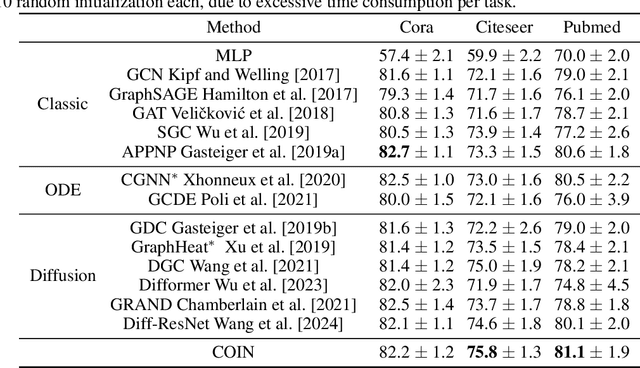
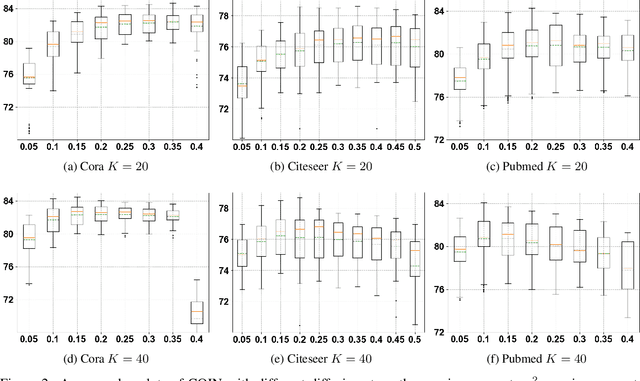
In this paper, we study the partial differential equation models of neural networks. Neural network can be viewed as a map from a simple base model to a complicate function. Based on solid analysis, we show that this map can be formulated by a convection-diffusion equation. This theoretically certified framework gives mathematical foundation and more understanding of neural networks. Moreover, based on the convection-diffusion equation model, we design a novel network structure, which incorporates diffusion mechanism into network architecture. Extensive experiments on both benchmark datasets and real-world applications validate the performance of the proposed model.

An axiomatized PDE model of deep neural networks

Inspired by the relation between deep neural network (DNN) and partial differential equations (PDEs), we study the general form of the PDE models of deep neural networks. To achieve this goal, we formulate DNN as an evolution operator from a simple base model. Based on several reasonable assumptions, we prove that the evolution operator is actually determined by convection-diffusion equation. This convection-diffusion equation model gives mathematical explanation for several effective networks. Moreover, we show that the convection-diffusion model improves the robustness and reduces the Rademacher complexity. Based on the convection-diffusion equation, we design a new training method for ResNets. Experiments validate the performance of the proposed method.

Diff-ResNets for Few-shot Learning -- an ODE Perspective

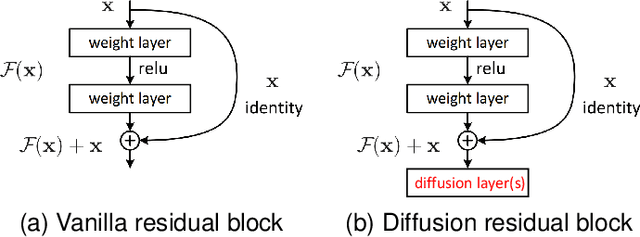
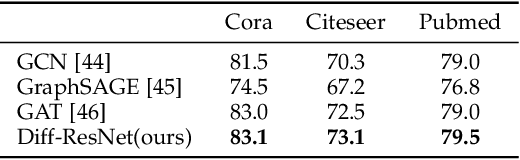
Interpreting deep neural networks from the ordinary differential equations (ODEs) perspective has inspired many efficient and robust network architectures. However, existing ODE based approaches ignore the relationship among data points, which is a critical component in many problems including few-shot learning and semi-supervised learning. In this paper, inspired by the diffusive ODEs, we propose a novel diffusion residual network (Diff-ResNet) to strengthen the interactions among data points. Under the structured data assumption, it is proved that the diffusion mechanism can decrease the distance-diameter ratio that improves the separability of inter-class points and reduces the distance among local intra-class points. This property can be easily adopted by the residual networks for constructing the separable hyperplanes. The synthetic binary classification experiments demonstrate the effectiveness of the proposed diffusion mechanism. Moreover, extensive experiments of few-shot image classification and semi-supervised graph node classification in various datasets validate the advantages of the proposed Diff-ResNet over existing few-shot learning methods.