Think Twice Before You Act: Improving Inverse Problem Solving With MCMC

Recent studies demonstrate that diffusion models can serve as a strong prior for solving inverse problems. A prominent example is Diffusion Posterior Sampling (DPS), which approximates the posterior distribution of data given the measure using Tweedie's formula. Despite the merits of being versatile in solving various inverse problems without re-training, the performance of DPS is hindered by the fact that this posterior approximation can be inaccurate especially for high noise levels. Therefore, we propose \textbf{D}iffusion \textbf{P}osterior \textbf{MC}MC (\textbf{DPMC}), a novel inference algorithm based on Annealed MCMC to solve inverse problems with pretrained diffusion models. We define a series of intermediate distributions inspired by the approximated conditional distributions used by DPS. Through annealed MCMC sampling, we encourage the samples to follow each intermediate distribution more closely before moving to the next distribution at a lower noise level, and therefore reduce the accumulated error along the path. We test our algorithm in various inverse problems, including super resolution, Gaussian deblurring, motion deblurring, inpainting, and phase retrieval. Our algorithm outperforms DPS with less number of evaluations across nearly all tasks, and is competitive among existing approaches.

From optimal score matching to optimal sampling

The recent, impressive advances in algorithmic generation of high-fidelity image, audio, and video are largely due to great successes in score-based diffusion models. A key implementing step is score matching, that is, the estimation of the score function of the forward diffusion process from training data. As shown in earlier literature, the total variation distance between the law of a sample generated from the trained diffusion model and the ground truth distribution can be controlled by the score matching risk. Despite the widespread use of score-based diffusion models, basic theoretical questions concerning exact optimal statistical rates for score estimation and its application to density estimation remain open. We establish the sharp minimax rate of score estimation for smooth, compactly supported densities. Formally, given \(n\) i.i.d. samples from an unknown \(\alpha\)-H\"{o}lder density \(f\) supported on \([-1, 1]\), we prove the minimax rate of estimating the score function of the diffused distribution \(f * \mathcal{N}(0, t)\) with respect to the score matching loss is \(\frac{1}{nt^2} \wedge \frac{1}{nt^{3/2}} \wedge (t^{\alpha-1} + n^{-2(\alpha-1)/(2\alpha+1)})\) for all \(\alpha > 0\) and \(t \ge 0\). As a consequence, it is shown the law \(\hat{f}\) of a sample generated from the diffusion model achieves the sharp minimax rate \(\bE(\dTV(\hat{f}, f)^2) \lesssim n^{-2\alpha/(2\alpha+1)}\) for all \(\alpha > 0\) without any extraneous logarithmic terms which are prevalent in the literature, and without the need for early stopping which has been required for all existing procedures to the best of our knowledge.

Diffusion Transformer Captures Spatial-Temporal Dependencies: A Theory for Gaussian Process Data

Diffusion Transformer, the backbone of Sora for video generation, successfully scales the capacity of diffusion models, pioneering new avenues for high-fidelity sequential data generation. Unlike static data such as images, sequential data consists of consecutive data frames indexed by time, exhibiting rich spatial and temporal dependencies. These dependencies represent the underlying dynamic model and are critical to validate the generated data. In this paper, we make the first theoretical step towards bridging diffusion transformers for capturing spatial-temporal dependencies. Specifically, we establish score approximation and distribution estimation guarantees of diffusion transformers for learning Gaussian process data with covariance functions of various decay patterns. We highlight how the spatial-temporal dependencies are captured and affect learning efficiency. Our study proposes a novel transformer approximation theory, where the transformer acts to unroll an algorithm. We support our theoretical results by numerical experiments, providing strong evidence that spatial-temporal dependencies are captured within attention layers, aligning with our approximation theory.

Provable Statistical Rates for Consistency Diffusion Models

Diffusion models have revolutionized various application domains, including computer vision and audio generation. Despite the state-of-the-art performance, diffusion models are known for their slow sample generation due to the extensive number of steps involved. In response, consistency models have been developed to merge multiple steps in the sampling process, thereby significantly boosting the speed of sample generation without compromising quality. This paper contributes towards the first statistical theory for consistency models, formulating their training as a distribution discrepancy minimization problem. Our analysis yields statistical estimation rates based on the Wasserstein distance for consistency models, matching those of vanilla diffusion models. Additionally, our results encompass the training of consistency models through both distillation and isolation methods, demystifying their underlying advantage.

Learning Narrow One-Hidden-Layer ReLU Networks

We consider the well-studied problem of learning a linear combination of $k$ ReLU activations with respect to a Gaussian distribution on inputs in $d$ dimensions. We give the first polynomial-time algorithm that succeeds whenever $k$ is a constant. All prior polynomial-time learners require additional assumptions on the network, such as positive combining coefficients or the matrix of hidden weight vectors being well-conditioned. Our approach is based on analyzing random contractions of higher-order moment tensors. We use a multi-scale analysis to argue that sufficiently close neurons can be collapsed together, sidestepping the conditioning issues present in prior work. This allows us to design an iterative procedure to discover individual neurons.

Understanding Value Decomposition Algorithms in Deep Cooperative Multi-Agent Reinforcement Learning

Value function decomposition is becoming a popular rule of thumb for scaling up multi-agent reinforcement learning (MARL) in cooperative games. For such a decomposition rule to hold, the assumption of the individual-global max (IGM) principle must be made; that is, the local maxima on the decomposed value function per every agent must amount to the global maximum on the joint value function. This principle, however, does not have to hold in general. As a result, the applicability of value decomposition algorithms is concealed and their corresponding convergence properties remain unknown. In this paper, we make the first effort to answer these questions. Specifically, we introduce the set of cooperative games in which the value decomposition methods find their validity, which is referred as decomposable games. In decomposable games, we theoretically prove that applying the multi-agent fitted Q-Iteration algorithm (MA-FQI) will lead to an optimal Q-function. In non-decomposable games, the estimated Q-function by MA-FQI can still converge to the optimum under the circumstance that the Q-function needs projecting into the decomposable function space at each iteration. In both settings, we consider value function representations by practical deep neural networks and derive their corresponding convergence rates. To summarize, our results, for the first time, offer theoretical insights for MARL practitioners in terms of when value decomposition algorithms converge and why they perform well.

On the One-sided Convergence of Adam-type Algorithms in Non-convex Non-concave Min-max Optimization

Adam-type methods, the extension of adaptive gradient methods, have shown great performance in the training of both supervised and unsupervised machine learning models. In particular, Adam-type optimizers have been widely used empirically as the default tool for training generative adversarial networks (GANs). On the theory side, however, despite the existence of theoretical results showing the efficiency of Adam-type methods in minimization problems, the reason of their wonderful performance still remains absent in GAN's training. In existing works, the fast convergence has long been considered as one of the most important reasons and multiple works have been proposed to give a theoretical guarantee of the convergence to a critical point of min-max optimization algorithms under certain assumptions. In this paper, we firstly argue empirically that in GAN's training, Adam does not converge to a critical point even upon successful training: Only the generator is converging while the discriminator's gradient norm remains high throughout the training. We name this one-sided convergence. Then we bridge the gap between experiments and theory by showing that Adam-type algorithms provably converge to a one-sided first order stationary points in min-max optimization problems under the one-sided MVI condition. We also empirically verify that such one-sided MVI condition is satisfied for standard GANs after trained over standard data sets. To the best of our knowledge, this is the very first result which provides an empirical observation and a strict theoretical guarantee on the one-sided convergence of Adam-type algorithms in min-max optimization.

Gap-Dependent Bounds for Two-Player Markov Games

As one of the most popular methods in the field of reinforcement learning, Q-learning has received increasing attention. Recently, there have been more theoretical works on the regret bound of algorithms that belong to the Q-learning class in different settings. In this paper, we analyze the cumulative regret when conducting Nash Q-learning algorithm on 2-player turn-based stochastic Markov games (2-TBSG), and propose the very first gap dependent logarithmic upper bounds in the episodic tabular setting. This bound matches the theoretical lower bound only up to a logarithmic term. Furthermore, we extend the conclusion to the discounted game setting with infinite horizon and propose a similar gap dependent logarithmic regret bound. Also, under the linear MDP assumption, we obtain another logarithmic regret for 2-TBSG, in both centralized and independent settings.

Diff-ResNets for Few-shot Learning -- an ODE Perspective

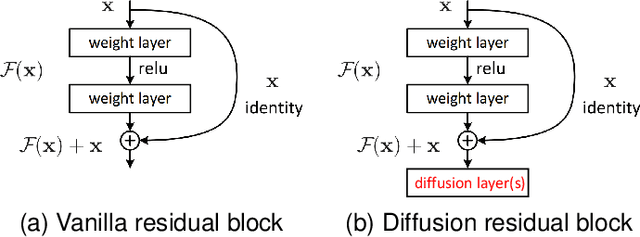
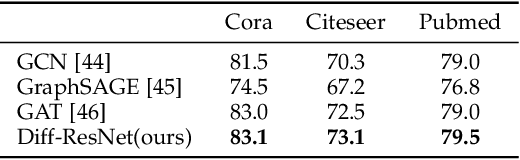
Interpreting deep neural networks from the ordinary differential equations (ODEs) perspective has inspired many efficient and robust network architectures. However, existing ODE based approaches ignore the relationship among data points, which is a critical component in many problems including few-shot learning and semi-supervised learning. In this paper, inspired by the diffusive ODEs, we propose a novel diffusion residual network (Diff-ResNet) to strengthen the interactions among data points. Under the structured data assumption, it is proved that the diffusion mechanism can decrease the distance-diameter ratio that improves the separability of inter-class points and reduces the distance among local intra-class points. This property can be easily adopted by the residual networks for constructing the separable hyperplanes. The synthetic binary classification experiments demonstrate the effectiveness of the proposed diffusion mechanism. Moreover, extensive experiments of few-shot image classification and semi-supervised graph node classification in various datasets validate the advantages of the proposed Diff-ResNet over existing few-shot learning methods.

When can Wasserstein GANs minimize Wasserstein Distance?

Generative Adversarial Networks (GANs) are widely used models to learn complex real-world distributions. In GANs, the training of the generator usually stops when the discriminator can no longer distinguish the generator's output from the set of training examples. A central question of GANs is that when the training stops, whether the generated distribution is actually close to the target distribution. Previously, it was found that such closeness can only be achieved when there is a strict capacity trade-off between the generator and discriminator: Neither of the two models can be too powerful than the other. In this paper, we established one of the first theoretical results in explaining this trade-off. We show that when the generator is a class of two-layer neural networks, then it is necessary and sufficient for the discriminator to be a one-layer network with ReLU-type activation functions. With this trade-off, using polynomially many training examples, when the training stops, the generator will indeed output a distribution that is inverse-polynomially close to the target. Our result also sheds light on how GANs training can find such a generator efficiently.