Sublinear iterations can suffice even for DDPMs

SDE-based methods such as denoising diffusion probabilistic models (DDPMs) have shown remarkable success in real-world sample generation tasks. Prior analyses of DDPMs have been focused on the exponential Euler discretization, showing guarantees that generally depend at least linearly on the dimension or initial Fisher information. Inspired by works in log-concave sampling (Shen and Lee, 2019), we analyze an integrator -- the denoising diffusion randomized midpoint method (DDRaM) -- that leverages an additional randomized midpoint to better approximate the SDE. Using a recently-developed analytic framework called the "shifted composition rule", we show that this algorithm enjoys favorable discretization properties under appropriate smoothness assumptions, with sublinear $\widetilde{O}(\sqrt{d})$ score evaluations needed to ensure convergence. This is the first sublinear complexity bound for pure DDPM sampling -- prior works which obtained such bounds worked instead with ODE-based sampling and had to make modifications to the sampler which deviate from how they are used in practice. We also provide experimental validation of the advantages of our method, showing that it performs well in practice with pre-trained image synthesis models.

Optimal Inference Schedules for Masked Diffusion Models

A major bottleneck of standard auto-regressive large language models is that their inference process is inherently sequential, resulting in very long and costly inference times. To circumvent this, practitioners proposed a class of language models called diffusion language models, of which the masked diffusion model (MDM) is the most successful. The MDM is able to sample tokens out-of-order and, ostensibly, many tokens at once and in parallel. However, there is very limited rigorous understanding of how much parallel sampling these models can perform without noticeable degradation in their sampling performance. Prior work of Li and Cai obtained some preliminary bounds, but these are not tight for many natural classes of distributions. In this work, we give a new, exact characterization of the expected divergence between the true distribution and the sampled distribution, for any distribution and any unmasking schedule for the sampler, showing an elegant connection to the theory of univariate function approximation. By leveraging this connection, we then attain a number of novel lower and upper bounds for this problem. While the connection to function approximation in principle gives the optimal unmasking schedule for any distribution, we show that it is in general impossible to compete with it without strong a priori knowledge of the distribution, even in seemingly benign settings. However, we also demonstrate new upper bounds and new sampling schedules in terms of well-studied information-theoretic properties of the base distribution, namely, its total correlation and dual total correlation, which show that in some natural settings, one can sample in $O(log n)$ steps without any visible loss in performance, where $n$ is the total sequence length.

Selective Underfitting in Diffusion Models

Diffusion models have emerged as the principal paradigm for generative modeling across various domains. During training, they learn the score function, which in turn is used to generate samples at inference. They raise a basic yet unsolved question: which score do they actually learn? In principle, a diffusion model that matches the empirical score in the entire data space would simply reproduce the training data, failing to generate novel samples. Recent work addresses this question by arguing that diffusion models underfit the empirical score due to training-time inductive biases. In this work, we refine this perspective, introducing the notion of selective underfitting: instead of underfitting the score everywhere, better diffusion models more accurately approximate the score in certain regions of input space, while underfitting it in others. We characterize these regions and design empirical interventions to validate our perspective. Our results establish that selective underfitting is essential for understanding diffusion models, yielding new, testable insights into their generalization and generative performance.

Fine-Tuning Masked Diffusion for Provable Self-Correction

A natural desideratum for generative models is self-correction--detecting and revising low-quality tokens at inference. While Masked Diffusion Models (MDMs) have emerged as a promising approach for generative modeling in discrete spaces, their capacity for self-correction remains poorly understood. Prior attempts to incorporate self-correction into MDMs either require overhauling MDM architectures/training or rely on imprecise proxies for token quality, limiting their applicability. Motivated by this, we introduce PRISM--Plug-in Remasking for Inference-time Self-correction of Masked Diffusions--a lightweight, model-agnostic approach that applies to any pretrained MDM. Theoretically, PRISM defines a self-correction loss that provably learns per-token quality scores, without RL or a verifier. These quality scores are computed in the same forward pass with MDM and used to detect low-quality tokens. Empirically, PRISM advances MDM inference across domains and scales: Sudoku; unconditional text (170M); and code with LLaDA (8B).

ReGuidance: A Simple Diffusion Wrapper for Boosting Sample Quality on Hard Inverse Problems

There has been a flurry of activity around using pretrained diffusion models as informed data priors for solving inverse problems, and more generally around steering these models using reward models. Training-free methods like diffusion posterior sampling (DPS) and its many variants have offered flexible heuristic algorithms for these tasks, but when the reward is not informative enough, e.g., in hard inverse problems with low signal-to-noise ratio, these techniques veer off the data manifold, failing to produce realistic outputs. In this work, we devise a simple wrapper, ReGuidance, for boosting both the sample realism and reward achieved by these methods. Given a candidate solution $\hat{x}$ produced by an algorithm of the user's choice, we propose inverting the solution by running the unconditional probability flow ODE in reverse starting from $\hat{x}$, and then using the resulting latent as an initialization for DPS. We evaluate our wrapper on hard inverse problems like large box in-painting and super-resolution with high upscaling. Whereas state-of-the-art baselines visibly fail, we find that applying our wrapper on top of these baselines significantly boosts sample quality and measurement consistency. We complement these findings with theory proving that on certain multimodal data distributions, ReGuidance simultaneously boosts the reward and brings the candidate solution closer to the data manifold. To our knowledge, this constitutes the first rigorous algorithmic guarantee for DPS.

Information-Computation Gaps in Quantum Learning via Low-Degree Likelihood

In a variety of physically relevant settings for learning from quantum data, designing protocols that can computationally efficiently extract information remains largely an art, and there are important cases where we believe this to be impossible, that is, where there is an information-computation gap. While there is a large array of tools in the classical literature for giving evidence for average-case hardness of statistical inference problems, the corresponding tools in the quantum literature are far more limited. One such framework in the classical literature, the low-degree method, makes predictions about hardness of inference problems based on the failure of estimators given by low-degree polynomials. In this work, we extend this framework to the quantum setting. We establish a general connection between state designs and low-degree hardness. We use this to obtain the first information-computation gaps for learning Gibbs states of random, sparse, non-local Hamiltonians. We also use it to prove hardness for learning random shallow quantum circuit states in a challenging model where states can be measured in adaptively chosen bases. To our knowledge, the ability to model adaptivity within the low-degree framework was open even in classical settings. In addition, we also obtain a low-degree hardness result for quantum error mitigation against strategies with single-qubit measurements. We define a new quantum generalization of the planted biclique problem and identify the threshold at which this problem becomes computationally hard for protocols that perform local measurements. Interestingly, the complexity landscape for this problem shifts when going from local measurements to more entangled single-copy measurements. We show average-case hardness for the "standard" variant of Learning Stabilizers with Noise and for agnostically learning product states.

S4S: Solving for a Diffusion Model Solver

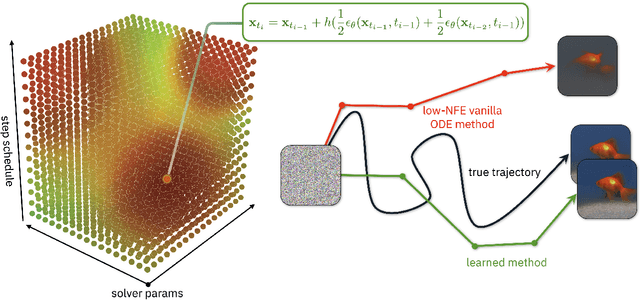
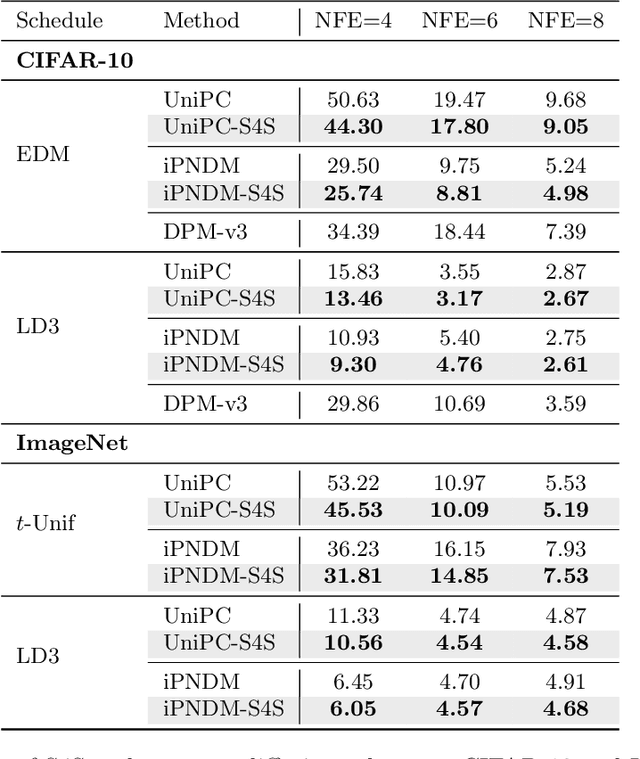
Diffusion models (DMs) create samples from a data distribution by starting from random noise and iteratively solving a reverse-time ordinary differential equation (ODE). Because each step in the iterative solution requires an expensive neural function evaluation (NFE), there has been significant interest in approximately solving these diffusion ODEs with only a few NFEs without modifying the underlying model. However, in the few NFE regime, we observe that tracking the true ODE evolution is fundamentally impossible using traditional ODE solvers. In this work, we propose a new method that learns a good solver for the DM, which we call Solving for the Solver (S4S). S4S directly optimizes a solver to obtain good generation quality by learning to match the output of a strong teacher solver. We evaluate S4S on six different pre-trained DMs, including pixel-space and latent-space DMs for both conditional and unconditional sampling. In all settings, S4S uniformly improves the sample quality relative to traditional ODE solvers. Moreover, our method is lightweight, data-free, and can be plugged in black-box on top of any discretization schedule or architecture to improve performance. Building on top of this, we also propose S4S-Alt, which optimizes both the solver and the discretization schedule. By exploiting the full design space of DM solvers, with 5 NFEs, we achieve an FID of 3.73 on CIFAR10 and 13.26 on MS-COCO, representing a $1.5\times$ improvement over previous training-free ODE methods.

Train for the Worst, Plan for the Best: Understanding Token Ordering in Masked Diffusions

In recent years, masked diffusion models (MDMs) have emerged as a promising alternative approach for generative modeling over discrete domains. Compared to autoregressive models (ARMs), MDMs trade off complexity at training time with flexibility at inference time. At training time, they must learn to solve an exponentially large number of infilling problems, but at inference time, they can decode tokens in essentially arbitrary order. In this work, we closely examine these two competing effects. On the training front, we theoretically and empirically demonstrate that MDMs indeed train on computationally intractable subproblems compared to their autoregressive counterparts. On the inference front, we show that a suitable strategy for adaptively choosing the token decoding order significantly enhances the capabilities of MDMs, allowing them to sidestep hard subproblems. On logic puzzles like Sudoku, we show that adaptive inference can boost solving accuracy in pretrained MDMs from $<7$% to $\approx 90$%, even outperforming ARMs with $7\times$ as many parameters and that were explicitly trained via teacher forcing to learn the right order of decoding.

Blink of an eye: a simple theory for feature localization in generative models

Large language models (LLMs) can exhibit undesirable and unexpected behavior in the blink of an eye. In a recent Anthropic demo, Claude switched from coding to Googling pictures of Yellowstone, and these sudden shifts in behavior have also been observed in reasoning patterns and jailbreaks. This phenomenon is not unique to autoregressive models: in diffusion models, key features of the final output are decided in narrow ``critical windows'' of the generation process. In this work we develop a simple, unifying theory to explain this phenomenon. We show that it emerges generically as the generation process localizes to a sub-population of the distribution it models. While critical windows have been studied at length in diffusion models, existing theory heavily relies on strong distributional assumptions and the particulars of Gaussian diffusion. In contrast to existing work our theory (1) applies to autoregressive and diffusion models; (2) makes no distributional assumptions; (3) quantitatively improves previous bounds even when specialized to diffusions; and (4) requires basic tools and no stochastic calculus or statistical physics-based machinery. We also identify an intriguing connection to the all-or-nothing phenomenon from statistical inference. Finally, we validate our predictions empirically for LLMs and find that critical windows often coincide with failures in problem solving for various math and reasoning benchmarks.

Adaptivity can help exponentially for shadow tomography

In recent years there has been significant interest in understanding the statistical complexity of learning from quantum data under the constraint that one can only make unentangled measurements. While a key challenge in establishing tight lower bounds in this setting is to deal with the fact that the measurements can be chosen in an adaptive fashion, a recurring theme has been that adaptivity offers little advantage over more straightforward, nonadaptive protocols. In this note, we offer a counterpoint to this. We show that for the basic task of shadow tomography, protocols that use adaptively chosen two-copy measurements can be exponentially more sample-efficient than any protocol that uses nonadaptive two-copy measurements.