Gradient dynamics for low-rank fine-tuning beyond kernels
Paper and Code
Nov 23, 2024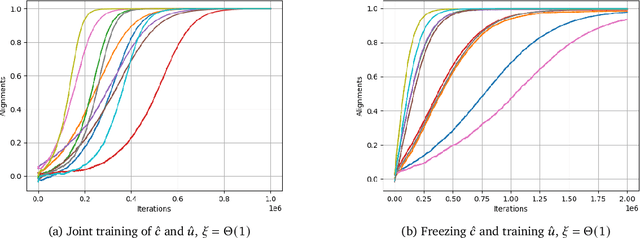
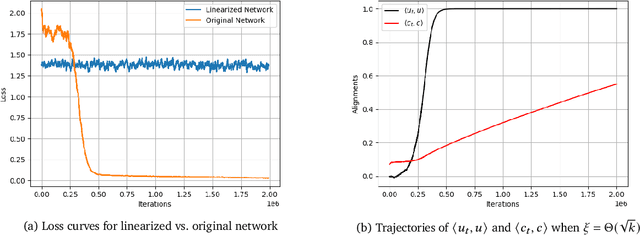
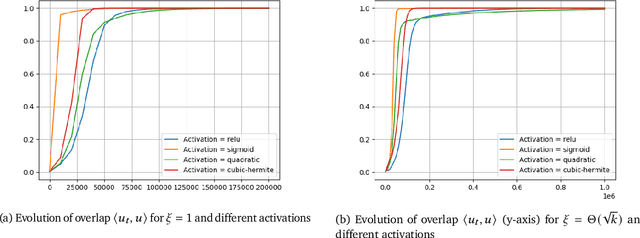
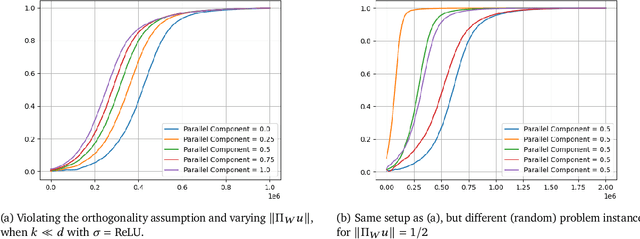
LoRA has emerged as one of the de facto methods for fine-tuning foundation models with low computational cost and memory footprint. The idea is to only train a low-rank perturbation to the weights of a pre-trained model, given supervised data for a downstream task. Despite its empirical sucess, from a mathematical perspective it remains poorly understood what learning mechanisms ensure that gradient descent converges to useful low-rank perturbations. In this work we study low-rank fine-tuning in a student-teacher setting. We are given the weights of a two-layer base model $f$, as well as i.i.d. samples $(x,f^*(x))$ where $x$ is Gaussian and $f^*$ is the teacher model given by perturbing the weights of $f$ by a rank-1 matrix. This generalizes the setting of generalized linear model (GLM) regression where the weights of $f$ are zero. When the rank-1 perturbation is comparable in norm to the weight matrix of $f$, the training dynamics are nonlinear. Nevertheless, in this regime we prove under mild assumptions that a student model which is initialized at the base model and trained with online gradient descent will converge to the teacher in $dk^{O(1)}$ iterations, where $k$ is the number of neurons in $f$. Importantly, unlike in the GLM setting, the complexity does not depend on fine-grained properties of the activation's Hermite expansion. We also prove that in our setting, learning the teacher model "from scratch'' can require significantly more iterations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge