Smoothed Analysis for Learning Concepts with Low Intrinsic Dimension

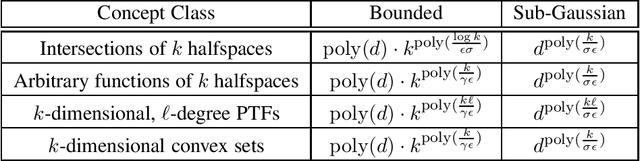
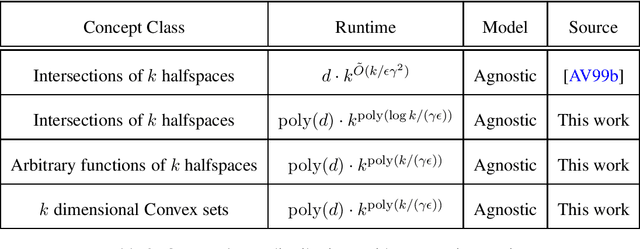
In traditional models of supervised learning, the goal of a learner -- given examples from an arbitrary joint distribution on $\mathbb{R}^d \times \{\pm 1\}$ -- is to output a hypothesis that is competitive (to within $\epsilon$) of the best fitting concept from some class. In order to escape strong hardness results for learning even simple concept classes, we introduce a smoothed-analysis framework that requires a learner to compete only with the best classifier that is robust to small random Gaussian perturbation. This subtle change allows us to give a wide array of learning results for any concept that (1) depends on a low-dimensional subspace (aka multi-index model) and (2) has a bounded Gaussian surface area. This class includes functions of halfspaces and (low-dimensional) convex sets, cases that are only known to be learnable in non-smoothed settings with respect to highly structured distributions such as Gaussians. Surprisingly, our analysis also yields new results for traditional non-smoothed frameworks such as learning with margin. In particular, we obtain the first algorithm for agnostically learning intersections of $k$-halfspaces in time $k^{poly(\frac{\log k}{\epsilon \gamma}) }$ where $\gamma$ is the margin parameter. Before our work, the best-known runtime was exponential in $k$ (Arriaga and Vempala, 1999).

Efficient Discrepancy Testing for Learning with Distribution Shift

A fundamental notion of distance between train and test distributions from the field of domain adaptation is discrepancy distance. While in general hard to compute, here we provide the first set of provably efficient algorithms for testing localized discrepancy distance, where discrepancy is computed with respect to a fixed output classifier. These results imply a broad set of new, efficient learning algorithms in the recently introduced model of Testable Learning with Distribution Shift (TDS learning) due to Klivans et al. (2023). Our approach generalizes and improves all prior work on TDS learning: (1) we obtain universal learners that succeed simultaneously for large classes of test distributions, (2) achieve near-optimal error rates, and (3) give exponential improvements for constant depth circuits. Our methods further extend to semi-parametric settings and imply the first positive results for low-dimensional convex sets. Additionally, we separate learning and testing phases and obtain algorithms that run in fully polynomial time at test time.

Online Learning of Halfspaces with Massart Noise

We study the task of online learning in the presence of Massart noise. Instead of assuming that the online adversary chooses an arbitrary sequence of labels, we assume that the context $\mathbf{x}$ is selected adversarially but the label $y$ presented to the learner disagrees with the ground-truth label of $\mathbf{x}$ with unknown probability at most $\eta$. We study the fundamental class of $\gamma$-margin linear classifiers and present a computationally efficient algorithm that achieves mistake bound $\eta T + o(T)$. Our mistake bound is qualitatively tight for efficient algorithms: it is known that even in the offline setting achieving classification error better than $\eta$ requires super-polynomial time in the SQ model. We extend our online learning model to a $k$-arm contextual bandit setting where the rewards -- instead of satisfying commonly used realizability assumptions -- are consistent (in expectation) with some linear ranking function with weight vector $\mathbf{w}^\ast$. Given a list of contexts $\mathbf{x}_1,\ldots \mathbf{x}_k$, if $\mathbf{w}^*\cdot \mathbf{x}_i > \mathbf{w}^* \cdot \mathbf{x}_j$, the expected reward of action $i$ must be larger than that of $j$ by at least $\Delta$. We use our Massart online learner to design an efficient bandit algorithm that obtains expected reward at least $(1-1/k)~ \Delta T - o(T)$ bigger than choosing a random action at every round.

Active Learning with Simple Questions

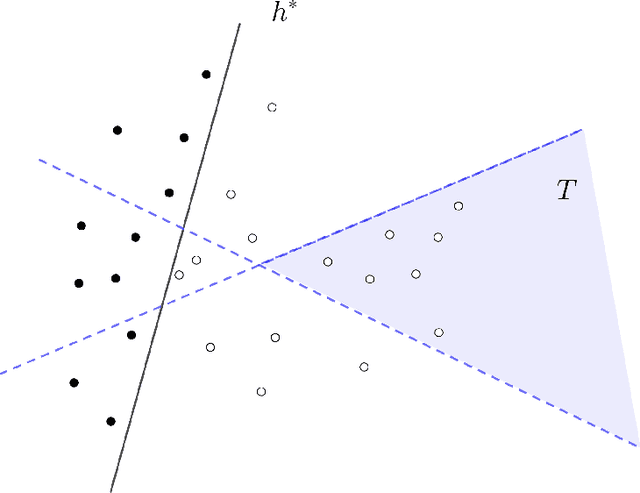
We consider an active learning setting where a learner is presented with a pool S of n unlabeled examples belonging to a domain X and asks queries to find the underlying labeling that agrees with a target concept h^* \in H. In contrast to traditional active learning that queries a single example for its label, we study more general region queries that allow the learner to pick a subset of the domain T \subset X and a target label y and ask a labeler whether h^*(x) = y for every example in the set T \cap S. Such more powerful queries allow us to bypass the limitations of traditional active learning and use significantly fewer rounds of interactions to learn but can potentially lead to a significantly more complex query language. Our main contribution is quantifying the trade-off between the number of queries and the complexity of the query language used by the learner. We measure the complexity of the region queries via the VC dimension of the family of regions. We show that given any hypothesis class H with VC dimension d, one can design a region query family Q with VC dimension O(d) such that for every set of n examples S \subset X and every h^* \in H, a learner can submit O(d log n) queries from Q to a labeler and perfectly label S. We show a matching lower bound by designing a hypothesis class H with VC dimension d and a dataset S \subset X of size n such that any learning algorithm using any query class with VC dimension O(d) must make poly(n) queries to label S perfectly. Finally, we focus on well-studied hypothesis classes including unions of intervals, high-dimensional boxes, and d-dimensional halfspaces, and obtain stronger results. In particular, we design learning algorithms that (i) are computationally efficient and (ii) work even when the queries are not answered based on the learner's pool of examples S but on some unknown superset L of S

Learning general Gaussian mixtures with efficient score matching

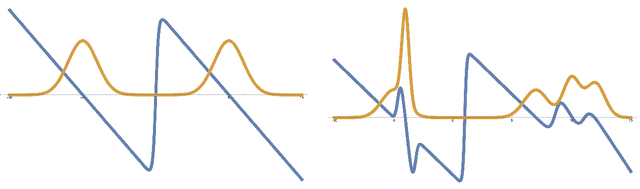
We study the problem of learning mixtures of $k$ Gaussians in $d$ dimensions. We make no separation assumptions on the underlying mixture components: we only require that the covariance matrices have bounded condition number and that the means and covariances lie in a ball of bounded radius. We give an algorithm that draws $d^{\mathrm{poly}(k/\varepsilon)}$ samples from the target mixture, runs in sample-polynomial time, and constructs a sampler whose output distribution is $\varepsilon$-far from the unknown mixture in total variation. Prior works for this problem either (i) required exponential runtime in the dimension $d$, (ii) placed strong assumptions on the instance (e.g., spherical covariances or clusterability), or (iii) had doubly exponential dependence on the number of components $k$. Our approach departs from commonly used techniques for this problem like the method of moments. Instead, we leverage a recently developed reduction, based on diffusion models, from distribution learning to a supervised learning task called score matching. We give an algorithm for the latter by proving a structural result showing that the score function of a Gaussian mixture can be approximated by a piecewise-polynomial function, and there is an efficient algorithm for finding it. To our knowledge, this is the first example of diffusion models achieving a state-of-the-art theoretical guarantee for an unsupervised learning task.

Super Non-singular Decompositions of Polynomials and their Application to Robustly Learning Low-degree PTFs

We study the efficient learnability of low-degree polynomial threshold functions (PTFs) in the presence of a constant fraction of adversarial corruptions. Our main algorithmic result is a polynomial-time PAC learning algorithm for this concept class in the strong contamination model under the Gaussian distribution with error guarantee $O_{d, c}(\text{opt}^{1-c})$, for any desired constant $c>0$, where $\text{opt}$ is the fraction of corruptions. In the strong contamination model, an omniscient adversary can arbitrarily corrupt an $\text{opt}$-fraction of the data points and their labels. This model generalizes the malicious noise model and the adversarial label noise model. Prior to our work, known polynomial-time algorithms in this corruption model (or even in the weaker adversarial label noise model) achieved error $\tilde{O}_d(\text{opt}^{1/(d+1)})$, which deteriorates significantly as a function of the degree $d$. Our algorithm employs an iterative approach inspired by localization techniques previously used in the context of learning linear threshold functions. Specifically, we use a robust perceptron algorithm to compute a good partial classifier and then iterate on the unclassified points. In order to achieve this, we need to take a set defined by a number of polynomial inequalities and partition it into several well-behaved subsets. To this end, we develop new polynomial decomposition techniques that may be of independent interest.

Agnostically Learning Multi-index Models with Queries

We study the power of query access for the task of agnostic learning under the Gaussian distribution. In the agnostic model, no assumptions are made on the labels and the goal is to compute a hypothesis that is competitive with the {\em best-fit} function in a known class, i.e., it achieves error $\mathrm{opt}+\epsilon$, where $\mathrm{opt}$ is the error of the best function in the class. We focus on a general family of Multi-Index Models (MIMs), which are $d$-variate functions that depend only on few relevant directions, i.e., have the form $g(\mathbf{W} \mathbf{x})$ for an unknown link function $g$ and a $k \times d$ matrix $\mathbf{W}$. Multi-index models cover a wide range of commonly studied function classes, including constant-depth neural networks with ReLU activations, and intersections of halfspaces. Our main result shows that query access gives significant runtime improvements over random examples for agnostically learning MIMs. Under standard regularity assumptions for the link function (namely, bounded variation or surface area), we give an agnostic query learner for MIMs with complexity $O(k)^{\mathrm{poly}(1/\epsilon)} \; \mathrm{poly}(d) $. In contrast, algorithms that rely only on random examples inherently require $d^{\mathrm{poly}(1/\epsilon)}$ samples and runtime, even for the basic problem of agnostically learning a single ReLU or a halfspace. Our algorithmic result establishes a strong computational separation between the agnostic PAC and the agnostic PAC+Query models under the Gaussian distribution. Prior to our work, no such separation was known -- even for the special case of agnostically learning a single halfspace, for which it was an open problem first posed by Feldman. Our results are enabled by a general dimension-reduction technique that leverages query access to estimate gradients of (a smoothed version of) the underlying label function.

Optimizing Solution-Samplers for Combinatorial Problems: The Landscape of Policy-Gradient Methods

Deep Neural Networks and Reinforcement Learning methods have empirically shown great promise in tackling challenging combinatorial problems. In those methods a deep neural network is used as a solution generator which is then trained by gradient-based methods (e.g., policy gradient) to successively obtain better solution distributions. In this work we introduce a novel theoretical framework for analyzing the effectiveness of such methods. We ask whether there exist generative models that (i) are expressive enough to generate approximately optimal solutions; (ii) have a tractable, i.e, polynomial in the size of the input, number of parameters; (iii) their optimization landscape is benign in the sense that it does not contain sub-optimal stationary points. Our main contribution is a positive answer to this question. Our result holds for a broad class of combinatorial problems including Max- and Min-Cut, Max-$k$-CSP, Maximum-Weight-Bipartite-Matching, and the Traveling Salesman Problem. As a byproduct of our analysis we introduce a novel regularization process over vanilla gradient descent and provide theoretical and experimental evidence that it helps address vanishing-gradient issues and escape bad stationary points.

Self-Directed Linear Classification

In online classification, a learner is presented with a sequence of examples and aims to predict their labels in an online fashion so as to minimize the total number of mistakes. In the self-directed variant, the learner knows in advance the pool of examples and can adaptively choose the order in which predictions are made. Here we study the power of choosing the prediction order and establish the first strong separation between worst-order and random-order learning for the fundamental task of linear classification. Prior to our work, such a separation was known only for very restricted concept classes, e.g., one-dimensional thresholds or axis-aligned rectangles. We present two main results. If $X$ is a dataset of $n$ points drawn uniformly at random from the $d$-dimensional unit sphere, we design an efficient self-directed learner that makes $O(d \log \log(n))$ mistakes and classifies the entire dataset. If $X$ is an arbitrary $d$-dimensional dataset of size $n$, we design an efficient self-directed learner that predicts the labels of $99\%$ of the points in $X$ with mistake bound independent of $n$. In contrast, under a worst- or random-ordering, the number of mistakes must be at least $\Omega(d \log n)$, even when the points are drawn uniformly from the unit sphere and the learner only needs to predict the labels for $1\%$ of them.

Efficient Testable Learning of Halfspaces with Adversarial Label Noise

We give the first polynomial-time algorithm for the testable learning of halfspaces in the presence of adversarial label noise under the Gaussian distribution. In the recently introduced testable learning model, one is required to produce a tester-learner such that if the data passes the tester, then one can trust the output of the robust learner on the data. Our tester-learner runs in time $\poly(d/\eps)$ and outputs a halfspace with misclassification error $O(\opt)+\eps$, where $\opt$ is the 0-1 error of the best fitting halfspace. At a technical level, our algorithm employs an iterative soft localization technique enhanced with appropriate testers to ensure that the data distribution is sufficiently similar to a Gaussian.