Sample Complexity Bounds for Robust Mean Estimation with Mean-Shift Contamination

We study the basic task of mean estimation in the presence of mean-shift contamination. In the mean-shift contamination model, an adversary is allowed to replace a small constant fraction of the clean samples by samples drawn from arbitrarily shifted versions of the base distribution. Prior work characterized the sample complexity of this task for the special cases of the Gaussian and Laplace distributions. Specifically, it was shown that consistent estimation is possible in these cases, a property that is provably impossible in Huber's contamination model. An open question posed in earlier work was to determine the sample complexity of mean estimation in the mean-shift contamination model for general base distributions. In this work, we study and essentially resolve this open question. Specifically, we show that, under mild spectral conditions on the characteristic function of the (potentially multivariate) base distribution, there exists a sample-efficient algorithm that estimates the target mean to any desired accuracy. We complement our upper bound with a qualitatively matching sample complexity lower bound. Our techniques make critical use of Fourier analysis, and in particular introduce the notion of a Fourier witness as an essential ingredient of our upper and lower bounds.

Testable Learning of General Halfspaces under Massart Noise

We study the algorithmic task of testably learning general Massart halfspaces under the Gaussian distribution. In the testable learning setting, the aim is the design of a tester-learner pair satisfying the following properties: (1) if the tester accepts, the learner outputs a hypothesis and a certificate that it achieves near-optimal error, and (2) it is highly unlikely that the tester rejects if the data satisfies the underlying assumptions. Our main result is the first testable learning algorithm for general halfspaces with Massart noise and Gaussian marginals. The complexity of our algorithm is $d^{\mathrm{polylog}(\min\{1/γ, 1/ε\})}$, where $ε$ is the excess error and $γ$ is the bias of the target halfspace, which qualitatively matches the known quasi-polynomial Statistical Query lower bound for the non-testable setting. The analysis of our algorithm hinges on a novel sandwiching polynomial approximation to the sign function with multiplicative error that may be of broader interest.

From Generative to Episodic: Sample-Efficient Replicable Reinforcement Learning

The epidemic failure of replicability across empirical science and machine learning has recently motivated the formal study of replicable learning algorithms [Impagliazzo et al. (2022)]. In batch settings where data comes from a fixed i.i.d. source (e.g., hypothesis testing, supervised learning), the design of data-efficient replicable algorithms is now more or less understood. In contrast, there remain significant gaps in our knowledge for control settings like reinforcement learning where an agent must interact directly with a shifting environment. Karbasi et. al show that with access to a generative model of an environment with $S$ states and $A$ actions (the RL 'batch setting'), replicably learning a near-optimal policy costs only $\tilde{O}(S^2A^2)$ samples. On the other hand, the best upper bound without a generative model jumps to $\tilde{O}(S^7 A^7)$ [Eaton et al. (2024)] due to the substantial difficulty of environment exploration. This gap raises a key question in the broader theory of replicability: Is replicable exploration inherently more expensive than batch learning? Is sample-efficient replicable RL even possible? In this work, we (nearly) resolve this problem (for low-horizon tabular MDPs): exploration is not a significant barrier to replicable learning! Our main result is a replicable RL algorithm on $\tilde{O}(S^2A)$ samples, bridging the gap between the generative and episodic settings. We complement this with a matching $\tilde{\Omega}(S^2A)$ lower bound in the generative setting (under the common parallel sampling assumption) and an unconditional lower bound in the episodic setting of $\tilde{\Omega}(S^2)$ showcasing the near-optimality of our algorithm with respect to the state space $S$.

Replicable Distribution Testing

We initiate a systematic investigation of distribution testing in the framework of algorithmic replicability. Specifically, given independent samples from a collection of probability distributions, the goal is to characterize the sample complexity of replicably testing natural properties of the underlying distributions. On the algorithmic front, we develop new replicable algorithms for testing closeness and independence of discrete distributions. On the lower bound front, we develop a new methodology for proving sample complexity lower bounds for replicable testing that may be of broader interest. As an application of our technique, we establish near-optimal sample complexity lower bounds for replicable uniformity testing -- answering an open question from prior work -- and closeness testing.

Batch List-Decodable Linear Regression via Higher Moments

We study the task of list-decodable linear regression using batches. A batch is called clean if it consists of i.i.d. samples from an unknown linear regression distribution. For a parameter $\alpha \in (0, 1/2)$, an unknown $\alpha$-fraction of the batches are clean and no assumptions are made on the remaining ones. The goal is to output a small list of vectors at least one of which is close to the true regressor vector in $\ell_2$-norm. [DJKS23] gave an efficient algorithm, under natural distributional assumptions, with the following guarantee. Assuming that the batch size $n$ satisfies $n \geq \tilde{\Omega}(\alpha^{-1})$ and the number of batches is $m = \mathrm{poly}(d, n, 1/\alpha)$, their algorithm runs in polynomial time and outputs a list of $O(1/\alpha^2)$ vectors at least one of which is $\tilde{O}(\alpha^{-1/2}/\sqrt{n})$ close to the target regressor. Here we design a new polynomial time algorithm with significantly stronger guarantees under the assumption that the low-degree moments of the covariates distribution are Sum-of-Squares (SoS) certifiably bounded. Specifically, for any constant $\delta>0$, as long as the batch size is $n \geq \Omega_{\delta}(\alpha^{-\delta})$ and the degree-$\Theta(1/\delta)$ moments of the covariates are SoS certifiably bounded, our algorithm uses $m = \mathrm{poly}((dn)^{1/\delta}, 1/\alpha)$ batches, runs in polynomial-time, and outputs an $O(1/\alpha)$-sized list of vectors one of which is $O(\alpha^{-\delta/2}/\sqrt{n})$ close to the target. That is, our algorithm achieves substantially smaller minimum batch size and final error, while achieving the optimal list size. Our approach uses higher-order moment information by carefully combining the SoS paradigm interleaved with an iterative method and a novel list pruning procedure. In the process, we give an SoS proof of the Marcinkiewicz-Zygmund inequality that may be of broader applicability.

Entangled Mean Estimation in High-Dimensions

We study the task of high-dimensional entangled mean estimation in the subset-of-signals model. Specifically, given $N$ independent random points $x_1,\ldots,x_N$ in $\mathbb{R}^D$ and a parameter $\alpha \in (0, 1)$ such that each $x_i$ is drawn from a Gaussian with mean $\mu$ and unknown covariance, and an unknown $\alpha$-fraction of the points have identity-bounded covariances, the goal is to estimate the common mean $\mu$. The one-dimensional version of this task has received significant attention in theoretical computer science and statistics over the past decades. Recent work [LY20; CV24] has given near-optimal upper and lower bounds for the one-dimensional setting. On the other hand, our understanding of even the information-theoretic aspects of the multivariate setting has remained limited. In this work, we design a computationally efficient algorithm achieving an information-theoretically near-optimal error. Specifically, we show that the optimal error (up to polylogarithmic factors) is $f(\alpha,N) + \sqrt{D/(\alpha N)}$, where the term $f(\alpha,N)$ is the error of the one-dimensional problem and the second term is the sub-Gaussian error rate. Our algorithmic approach employs an iterative refinement strategy, whereby we progressively learn more accurate approximations $\hat \mu$ to $\mu$. This is achieved via a novel rejection sampling procedure that removes points significantly deviating from $\hat \mu$, as an attempt to filter out unusually noisy samples. A complication that arises is that rejection sampling introduces bias in the distribution of the remaining points. To address this issue, we perform a careful analysis of the bias, develop an iterative dimension-reduction strategy, and employ a novel subroutine inspired by list-decodable learning that leverages the one-dimensional result.

Don't Look Twice: Faster Video Transformers with Run-Length Tokenization

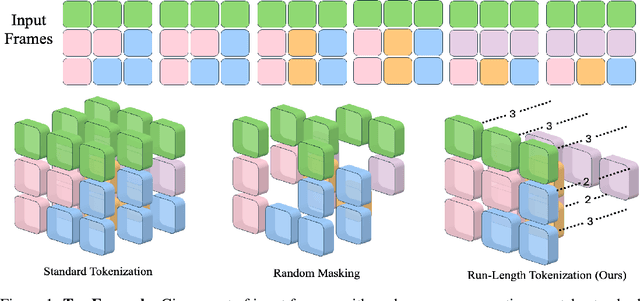
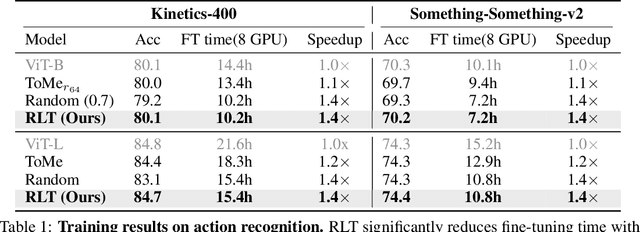
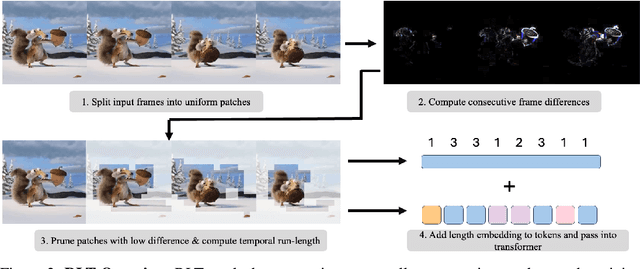
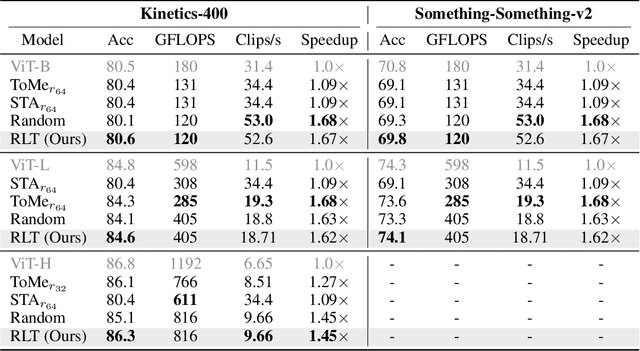
Transformers are slow to train on videos due to extremely large numbers of input tokens, even though many video tokens are repeated over time. Existing methods to remove such uninformative tokens either have significant overhead, negating any speedup, or require tuning for different datasets and examples. We present Run-Length Tokenization (RLT), a simple approach to speed up video transformers inspired by run-length encoding for data compression. RLT efficiently finds and removes runs of patches that are repeated over time prior to model inference, then replaces them with a single patch and a positional encoding to represent the resulting token's new length. Our method is content-aware, requiring no tuning for different datasets, and fast, incurring negligible overhead. RLT yields a large speedup in training, reducing the wall-clock time to fine-tune a video transformer by 30% while matching baseline model performance. RLT also works without any training, increasing model throughput by 35% with only 0.1% drop in accuracy. RLT speeds up training at 30 FPS by more than 100%, and on longer video datasets, can reduce the token count by up to 80%. Our project page is at https://rccchoudhury.github.io/projects/rlt/.

Replicable Uniformity Testing

Uniformity testing is arguably one of the most fundamental distribution testing problems. Given sample access to an unknown distribution $\mathbf{p}$ on $[n]$, one must decide if $\mathbf{p}$ is uniform or $\varepsilon$-far from uniform (in total variation distance). A long line of work established that uniformity testing has sample complexity $\Theta(\sqrt{n}\varepsilon^{-2})$. However, when the input distribution is neither uniform nor far from uniform, known algorithms may have highly non-replicable behavior. Consequently, if these algorithms are applied in scientific studies, they may lead to contradictory results that erode public trust in science. In this work, we revisit uniformity testing under the framework of algorithmic replicability [STOC '22], requiring the algorithm to be replicable under arbitrary distributions. While replicability typically incurs a $\rho^{-2}$ factor overhead in sample complexity, we obtain a replicable uniformity tester using only $\tilde{O}(\sqrt{n} \varepsilon^{-2} \rho^{-1})$ samples. To our knowledge, this is the first replicable learning algorithm with (nearly) linear dependence on $\rho$. Lastly, we consider a class of ``symmetric" algorithms [FOCS '00] whose outputs are invariant under relabeling of the domain $[n]$, which includes all existing uniformity testers (including ours). For this natural class of algorithms, we prove a nearly matching sample complexity lower bound for replicable uniformity testing.

Efficient Testable Learning of General Halfspaces with Adversarial Label Noise

We study the task of testable learning of general -- not necessarily homogeneous -- halfspaces with adversarial label noise with respect to the Gaussian distribution. In the testable learning framework, the goal is to develop a tester-learner such that if the data passes the tester, then one can trust the output of the robust learner on the data.Our main result is the first polynomial time tester-learner for general halfspaces that achieves dimension-independent misclassification error. At the heart of our approach is a new methodology to reduce testable learning of general halfspaces to testable learning of nearly homogeneous halfspaces that may be of broader interest.

Replicability in High Dimensional Statistics

The replicability crisis is a major issue across nearly all areas of empirical science, calling for the formal study of replicability in statistics. Motivated in this context, [Impagliazzo, Lei, Pitassi, and Sorrell STOC 2022] introduced the notion of replicable learning algorithms, and gave basic procedures for $1$-dimensional tasks including statistical queries. In this work, we study the computational and statistical cost of replicability for several fundamental high dimensional statistical tasks, including multi-hypothesis testing and mean estimation. Our main contribution establishes a computational and statistical equivalence between optimal replicable algorithms and high dimensional isoperimetric tilings. As a consequence, we obtain matching sample complexity upper and lower bounds for replicable mean estimation of distributions with bounded covariance, resolving an open problem of [Bun, Gaboardi, Hopkins, Impagliazzo, Lei, Pitassi, Sivakumar, and Sorrell, STOC2023] and for the $N$-Coin Problem, resolving a problem of [Karbasi, Velegkas, Yang, and Zhou, NeurIPS2023] up to log factors. While our equivalence is computational, allowing us to shave log factors in sample complexity from the best known efficient algorithms, efficient isoperimetric tilings are not known. To circumvent this, we introduce several relaxed paradigms that do allow for sample and computationally efficient algorithms, including allowing pre-processing, adaptivity, and approximate replicability. In these cases we give efficient algorithms matching or beating the best known sample complexity for mean estimation and the coin problem, including a generic procedure that reduces the standard quadratic overhead of replicability to linear in expectation.