Replicable Uniformity Testing

Uniformity testing is arguably one of the most fundamental distribution testing problems. Given sample access to an unknown distribution $\mathbf{p}$ on $[n]$, one must decide if $\mathbf{p}$ is uniform or $\varepsilon$-far from uniform (in total variation distance). A long line of work established that uniformity testing has sample complexity $\Theta(\sqrt{n}\varepsilon^{-2})$. However, when the input distribution is neither uniform nor far from uniform, known algorithms may have highly non-replicable behavior. Consequently, if these algorithms are applied in scientific studies, they may lead to contradictory results that erode public trust in science. In this work, we revisit uniformity testing under the framework of algorithmic replicability [STOC '22], requiring the algorithm to be replicable under arbitrary distributions. While replicability typically incurs a $\rho^{-2}$ factor overhead in sample complexity, we obtain a replicable uniformity tester using only $\tilde{O}(\sqrt{n} \varepsilon^{-2} \rho^{-1})$ samples. To our knowledge, this is the first replicable learning algorithm with (nearly) linear dependence on $\rho$. Lastly, we consider a class of ``symmetric" algorithms [FOCS '00] whose outputs are invariant under relabeling of the domain $[n]$, which includes all existing uniformity testers (including ours). For this natural class of algorithms, we prove a nearly matching sample complexity lower bound for replicable uniformity testing.

Replicability in High Dimensional Statistics

The replicability crisis is a major issue across nearly all areas of empirical science, calling for the formal study of replicability in statistics. Motivated in this context, [Impagliazzo, Lei, Pitassi, and Sorrell STOC 2022] introduced the notion of replicable learning algorithms, and gave basic procedures for $1$-dimensional tasks including statistical queries. In this work, we study the computational and statistical cost of replicability for several fundamental high dimensional statistical tasks, including multi-hypothesis testing and mean estimation. Our main contribution establishes a computational and statistical equivalence between optimal replicable algorithms and high dimensional isoperimetric tilings. As a consequence, we obtain matching sample complexity upper and lower bounds for replicable mean estimation of distributions with bounded covariance, resolving an open problem of [Bun, Gaboardi, Hopkins, Impagliazzo, Lei, Pitassi, Sivakumar, and Sorrell, STOC2023] and for the $N$-Coin Problem, resolving a problem of [Karbasi, Velegkas, Yang, and Zhou, NeurIPS2023] up to log factors. While our equivalence is computational, allowing us to shave log factors in sample complexity from the best known efficient algorithms, efficient isoperimetric tilings are not known. To circumvent this, we introduce several relaxed paradigms that do allow for sample and computationally efficient algorithms, including allowing pre-processing, adaptivity, and approximate replicability. In these cases we give efficient algorithms matching or beating the best known sample complexity for mean estimation and the coin problem, including a generic procedure that reduces the standard quadratic overhead of replicability to linear in expectation.

The I/O Complexity of Attention, or How Optimal is Flash Attention?

Self-attention is at the heart of the popular Transformer architecture, yet suffers from quadratic time and memory complexity. The breakthrough FlashAttention algorithm revealed I/O complexity as the true bottleneck in scaling Transformers. Given two levels of memory hierarchy, a fast cache (e.g. GPU on-chip SRAM) and a slow memory (e.g. GPU high-bandwidth memory), the I/O complexity measures the number of accesses to memory. FlashAttention computes attention using $\frac{N^2d^2}{M}$ I/O operations where $N$ is the dimension of the attention matrix, $d$ the head-dimension and $M$ the cache size. However, is this I/O complexity optimal? The known lower bound only rules out an I/O complexity of $o(Nd)$ when $M=\Theta(Nd)$, since the output that needs to be written to slow memory is $\Omega(Nd)$. This leads to the main question of our work: Is FlashAttention I/O optimal for all values of $M$? We resolve the above question in its full generality by showing an I/O complexity lower bound that matches the upper bound provided by FlashAttention for any values of $M \geq d^2$ within any constant factors. Further, we give a better algorithm with lower I/O complexity for $M < d^2$, and show that it is optimal as well. Moreover, our lower bounds do not rely on using combinatorial matrix multiplication for computing the attention matrix. We show even if one uses fast matrix multiplication, the above I/O complexity bounds cannot be improved. We do so by introducing a new communication complexity protocol for matrix compression, and connecting communication complexity to I/O complexity. To the best of our knowledge, this is the first work to establish a connection between communication complexity and I/O complexity, and we believe this connection could be of independent interest and will find many more applications in proving I/O complexity lower bounds in the future.

Predicting the Stereoselectivity of Chemical Transformations by Machine Learning

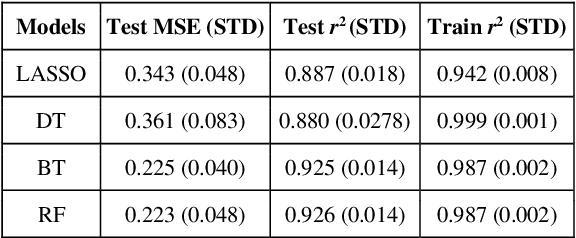
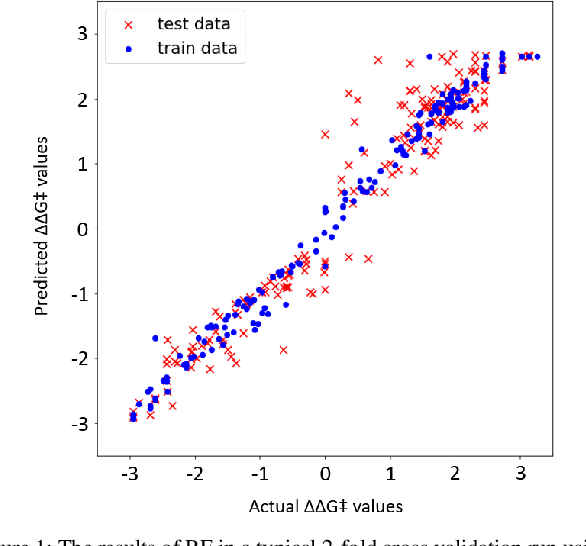
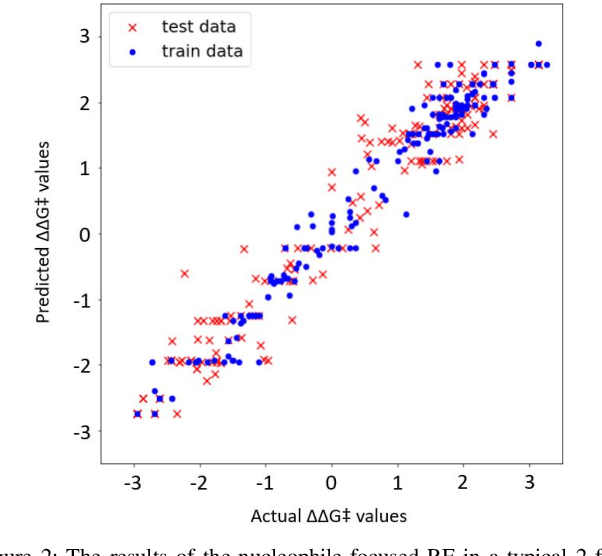
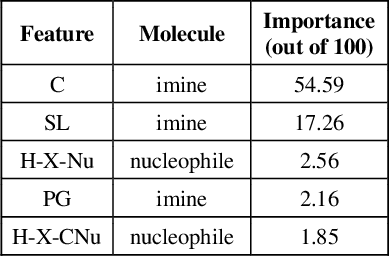
Stereoselective reactions (both chemical and enzymatic reactions) have been essential for origin of life, evolution, human biology and medicine. Since late 1960s, there have been numerous successes in the exciting new frontier of asymmetric catalysis. However, most industrial and academic asymmetric catalysis nowadays do follow the trial-and-error model, since the energetic difference for success or failure in asymmetric catalysis is incredibly small. Our current understanding about stereoselective reactions is mostly qualitative that stereoselectivity arises from differences in steric effects and electronic effects in multiple competing mechanistic pathways. Quantitatively understanding and modulating the stereoselectivity of for a given chemical reaction still remains extremely difficult. As a proof of principle, we herein present a novel machine learning technique, which combines a LASSO model and two Random Forest model via two Gaussian Mixture models, for quantitatively predicting stereoselectivity of chemical reactions. Compared to the recent ground-breaking approach [1], our approach is able to capture interactions between features and exploit complex data distributions, which are important for predicting stereoselectivity. Experimental results on a recently published dataset demonstrate that our approach significantly outperform [1]. The insight obtained from our results provide a solid foundation for further exploration of other synthetically valuable yet mechanistically intriguing stereoselective reactions.