From Generative to Episodic: Sample-Efficient Replicable Reinforcement Learning

The epidemic failure of replicability across empirical science and machine learning has recently motivated the formal study of replicable learning algorithms [Impagliazzo et al. (2022)]. In batch settings where data comes from a fixed i.i.d. source (e.g., hypothesis testing, supervised learning), the design of data-efficient replicable algorithms is now more or less understood. In contrast, there remain significant gaps in our knowledge for control settings like reinforcement learning where an agent must interact directly with a shifting environment. Karbasi et. al show that with access to a generative model of an environment with $S$ states and $A$ actions (the RL 'batch setting'), replicably learning a near-optimal policy costs only $\tilde{O}(S^2A^2)$ samples. On the other hand, the best upper bound without a generative model jumps to $\tilde{O}(S^7 A^7)$ [Eaton et al. (2024)] due to the substantial difficulty of environment exploration. This gap raises a key question in the broader theory of replicability: Is replicable exploration inherently more expensive than batch learning? Is sample-efficient replicable RL even possible? In this work, we (nearly) resolve this problem (for low-horizon tabular MDPs): exploration is not a significant barrier to replicable learning! Our main result is a replicable RL algorithm on $\tilde{O}(S^2A)$ samples, bridging the gap between the generative and episodic settings. We complement this with a matching $\tilde{\Omega}(S^2A)$ lower bound in the generative setting (under the common parallel sampling assumption) and an unconditional lower bound in the episodic setting of $\tilde{\Omega}(S^2)$ showcasing the near-optimality of our algorithm with respect to the state space $S$.

Replicability is Asymptotically Free in Multi-armed Bandits

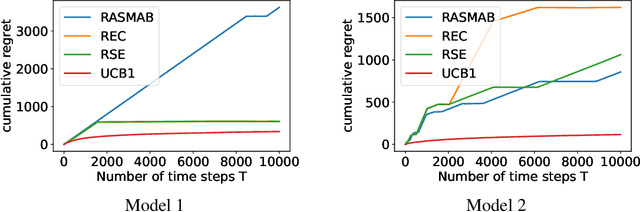
This work is motivated by the growing demand for reproducible machine learning. We study the stochastic multi-armed bandit problem. In particular, we consider a replicable algorithm that ensures, with high probability, that the algorithm's sequence of actions is not affected by the randomness inherent in the dataset. We observe that existing algorithms require $O(1/\rho^2)$ times more regret than nonreplicable algorithms, where $\rho$ is the level of nonreplication. However, we demonstrate that this additional cost is unnecessary when the time horizon $T$ is sufficiently large for a given $\rho$, provided that the magnitude of the confidence bounds is chosen carefully. We introduce an explore-then-commit algorithm that draws arms uniformly before committing to a single arm. Additionally, we examine a successive elimination algorithm that eliminates suboptimal arms at the end of each phase. To ensure the replicability of these algorithms, we incorporate randomness into their decision-making processes. We extend the use of successive elimination to the linear bandit problem as well. For the analysis of these algorithms, we propose a principled approach to limiting the probability of nonreplication. This approach elucidates the steps that existing research has implicitly followed. Furthermore, we derive the first lower bound for the two-armed replicable bandit problem, which implies the optimality of the proposed algorithms up to a $\log\log T$ factor for the two-armed case.

General Transformation for Consistent Online Approximation Algorithms

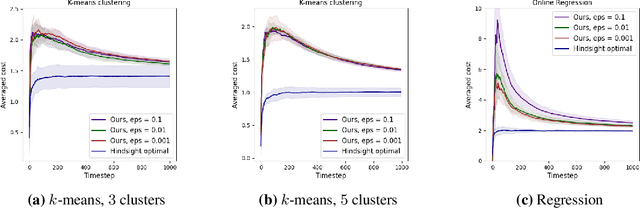
We introduce a transformation framework that can be utilized to develop online algorithms with low $\epsilon$-approximate regret in the random-order model from offline approximation algorithms. We first give a general reduction theorem that transforms an offline approximation algorithm with low average sensitivity to an online algorithm with low $\epsilon$-approximate regret. We then demonstrate that offline approximation algorithms can be transformed into a low-sensitivity version using a coreset construction method. To showcase the versatility of our approach, we apply it to various problems, including online $(k,z)$-clustering, online matrix approximation, and online regression, and successfully achieve polylogarithmic $\epsilon$-approximate regret for each problem. Moreover, we show that in all three cases, our algorithm also enjoys low inconsistency, which may be desired in some online applications.

Controlling Posterior Collapse by an Inverse Lipschitz Constraint on the Decoder Network

Variational autoencoders (VAEs) are one of the deep generative models that have experienced enormous success over the past decades. However, in practice, they suffer from a problem called posterior collapse, which occurs when the encoder coincides, or collapses, with the prior taking no information from the latent structure of the input data into consideration. In this work, we introduce an inverse Lipschitz neural network into the decoder and, based on this architecture, provide a new method that can control in a simple and clear manner the degree of posterior collapse for a wide range of VAE models equipped with a concrete theoretical guarantee. We also illustrate the effectiveness of our method through several numerical experiments.

Sparsification of Decomposable Submodular Functions

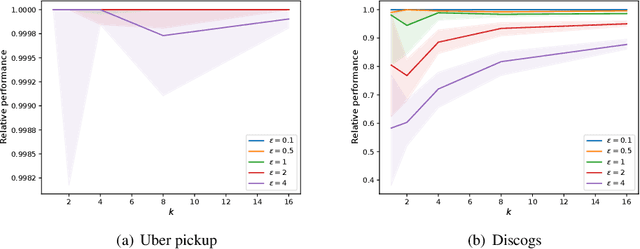
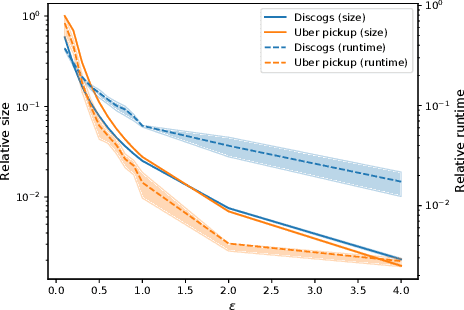
Submodular functions are at the core of many machine learning and data mining tasks. The underlying submodular functions for many of these tasks are decomposable, i.e., they are sum of several simple submodular functions. In many data intensive applications, however, the number of underlying submodular functions in the original function is so large that we need prohibitively large amount of time to process it and/or it does not even fit in the main memory. To overcome this issue, we introduce the notion of sparsification for decomposable submodular functions whose objective is to obtain an accurate approximation of the original function that is a (weighted) sum of only a few submodular functions. Our main result is a polynomial-time randomized sparsification algorithm such that the expected number of functions used in the output is independent of the number of underlying submodular functions in the original function. We also study the effectiveness of our algorithm under various constraints such as matroid and cardinality constraints. We complement our theoretical analysis with an empirical study of the performance of our algorithm.

Local Algorithms for Estimating Effective Resistance

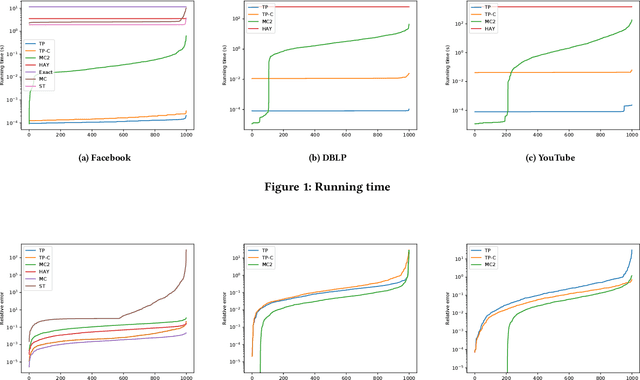
Effective resistance is an important metric that measures the similarity of two vertices in a graph. It has found applications in graph clustering, recommendation systems and network reliability, among others. In spite of the importance of the effective resistances, we still lack efficient algorithms to exactly compute or approximate them on massive graphs. In this work, we design several \emph{local algorithms} for estimating effective resistances, which are algorithms that only read a small portion of the input while still having provable performance guarantees. To illustrate, our main algorithm approximates the effective resistance between any vertex pair $s,t$ with an arbitrarily small additive error $\varepsilon$ in time $O(\mathrm{poly}(\log n/\varepsilon))$, whenever the underlying graph has bounded mixing time. We perform an extensive empirical study on several benchmark datasets, validating the performance of our algorithms.

RelWalk A Latent Variable Model Approach to Knowledge Graph Embedding

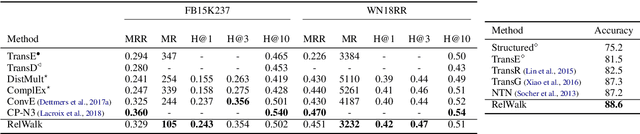
Embedding entities and relations of a knowledge graph in a low-dimensional space has shown impressive performance in predicting missing links between entities. Although progresses have been achieved, existing methods are heuristically motivated and theoretical understanding of such embeddings is comparatively underdeveloped. This paper extends the random walk model (Arora et al., 2016a) of word embeddings to Knowledge Graph Embeddings (KGEs) to derive a scoring function that evaluates the strength of a relation R between two entities h (head) and t (tail). Moreover, we show that marginal loss minimisation, a popular objective used in much prior work in KGE, follows naturally from the log-likelihood ratio maximisation under the probabilities estimated from the KGEs according to our theoretical relationship. We propose a learning objective motivated by the theoretical analysis to learn KGEs from a given knowledge graph. Using the derived objective, accurate KGEs are learnt from FB15K237 and WN18RR benchmark datasets, providing empirical evidence in support of the theory.

Downsampling for Testing and Learning in Product Distributions

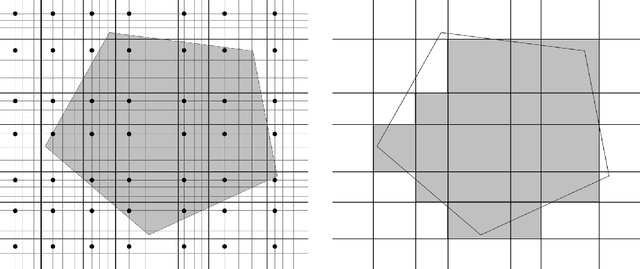
We study the domain reduction problem of eliminating dependence on $n$ from the complexity of property testing and learning algorithms on domain $[n]^d$, and the related problem of establishing testing and learning results for product distributions over $\mathbb{R}^d$. Our method, which we call downsampling, gives conceptually simple proofs for several results: 1. A 1-page proof of the recent $o(d)$-query monotonicity tester for the hypergrid (Black, Chakrabarty & Seshadhri, SODA 2020), and an improvement from $O(d^7)$ to $\widetilde O(d^4)$ in the sample complexity of their distribution-free monotonicity tester for product distributions over $\mathbb{R}^d$; 2. An $\exp(\widetilde O(kd))$-time agnostic learning algorithm for functions of $k$ convex sets in product distributions; 3. A polynomial-time agnostic learning algorithm for functions of a constant number of halfspaces in product distributions; 4. A polynomial-time agnostic learning algorithm for constant-degree polynomial threshold functions in product distributions; 5. An $\exp(\widetilde O(k \sqrt d))$-time agnostic learning algorithm for $k$-alternating functions in product distributions.

Fast and Private Submodular and $k$-Submodular Functions Maximization with Matroid Constraints

The problem of maximizing nonnegative monotone submodular functions under a certain constraint has been intensively studied in the last decade, and a wide range of efficient approximation algorithms have been developed for this problem. Many machine learning problems, including data summarization and influence maximization, can be naturally modeled as the problem of maximizing monotone submodular functions. However, when such applications involve sensitive data about individuals, their privacy concerns should be addressed. In this paper, we study the problem of maximizing monotone submodular functions subject to matroid constraints in the framework of differential privacy. We provide $(1-\frac{1}{\mathrm{e}})$-approximation algorithm which improves upon the previous results in terms of approximation guarantee. This is done with an almost cubic number of function evaluations in our algorithm. Moreover, we study $k$-submodularity, a natural generalization of submodularity. We give the first $\frac{1}{2}$-approximation algorithm that preserves differential privacy for maximizing monotone $k$-submodular functions subject to matroid constraints. The approximation ratio is asymptotically tight and is obtained with an almost linear number of function evaluations.

Hypergraph Clustering Based on PageRank

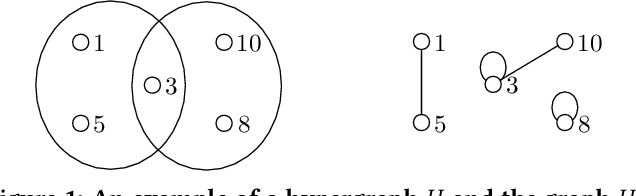
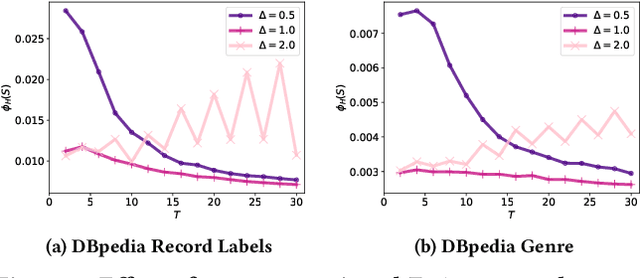
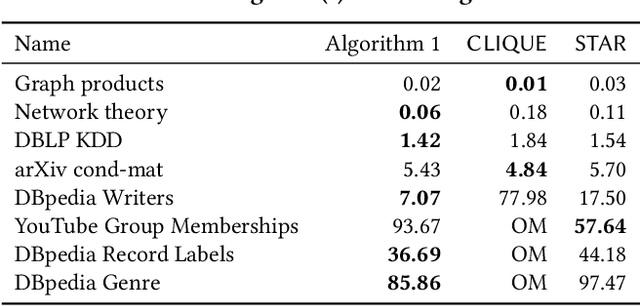
A hypergraph is a useful combinatorial object to model ternary or higher-order relations among entities. Clustering hypergraphs is a fundamental task in network analysis. In this study, we develop two clustering algorithms based on personalized PageRank on hypergraphs. The first one is local in the sense that its goal is to find a tightly connected vertex set with a bounded volume including a specified vertex. The second one is global in the sense that its goal is to find a tightly connected vertex set. For both algorithms, we discuss theoretical guarantees on the conductance of the output vertex set. Also, we experimentally demonstrate that our clustering algorithms outperform existing methods in terms of both the solution quality and running time. To the best of our knowledge, ours are the first practical algorithms for hypergraphs with theoretical guarantees on the conductance of the output set.