General Transformation for Consistent Online Approximation Algorithms

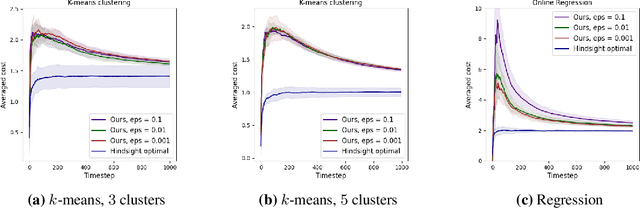
We introduce a transformation framework that can be utilized to develop online algorithms with low $\epsilon$-approximate regret in the random-order model from offline approximation algorithms. We first give a general reduction theorem that transforms an offline approximation algorithm with low average sensitivity to an online algorithm with low $\epsilon$-approximate regret. We then demonstrate that offline approximation algorithms can be transformed into a low-sensitivity version using a coreset construction method. To showcase the versatility of our approach, we apply it to various problems, including online $(k,z)$-clustering, online matrix approximation, and online regression, and successfully achieve polylogarithmic $\epsilon$-approximate regret for each problem. Moreover, we show that in all three cases, our algorithm also enjoys low inconsistency, which may be desired in some online applications.