Testing Juntas Optimally with Samples

We prove tight upper and lower bounds of $\Theta\left(\tfrac{1}{\epsilon}\left( \sqrt{2^k \log\binom{n}{k} } + \log\binom{n}{k} \right)\right)$ on the number of samples required for distribution-free $k$-junta testing. This is the first tight bound for testing a natural class of Boolean functions in the distribution-free sample-based model. Our bounds also hold for the feature selection problem, showing that a junta tester must learn the set of relevant variables. For tolerant junta testing, we prove a sample lower bound of $\Omega(2^{(1-o(1)) k} + \log\binom{n}{k})$ showing that, unlike standard testing, there is no large gap between tolerant testing and learning.

Testing Support Size More Efficiently Than Learning Histograms

Consider two problems about an unknown probability distribution $p$: 1. How many samples from $p$ are required to test if $p$ is supported on $n$ elements or not? Specifically, given samples from $p$, determine whether it is supported on at most $n$ elements, or it is "$\epsilon$-far" (in total variation distance) from being supported on $n$ elements. 2. Given $m$ samples from $p$, what is the largest lower bound on its support size that we can produce? The best known upper bound for problem (1) uses a general algorithm for learning the histogram of the distribution $p$, which requires $\Theta(\tfrac{n}{\epsilon^2 \log n})$ samples. We show that testing can be done more efficiently than learning the histogram, using only $O(\tfrac{n}{\epsilon \log n} \log(1/\epsilon))$ samples, nearly matching the best known lower bound of $\Omega(\tfrac{n}{\epsilon \log n})$. This algorithm also provides a better solution to problem (2), producing larger lower bounds on support size than what follows from previous work. The proof relies on an analysis of Chebyshev polynomial approximations outside the range where they are designed to be good approximations, and the paper is intended as an accessible self-contained exposition of the Chebyshev polynomial method.

VC Dimension and Distribution-Free Sample-Based Testing

We consider the problem of determining which classes of functions can be tested more efficiently than they can be learned, in the distribution-free sample-based model that corresponds to the standard PAC learning setting. Our main result shows that while VC dimension by itself does not always provide tight bounds on the number of samples required to test a class of functions in this model, it can be combined with a closely-related variant that we call "lower VC" (or LVC) dimension to obtain strong lower bounds on this sample complexity. We use this result to obtain strong and in many cases nearly optimal lower bounds on the sample complexity for testing unions of intervals, halfspaces, intersections of halfspaces, polynomial threshold functions, and decision trees. Conversely, we show that two natural classes of functions, juntas and monotone functions, can be tested with a number of samples that is polynomially smaller than the number of samples required for PAC learning. Finally, we also use the connection between VC dimension and property testing to establish new lower bounds for testing radius clusterability and testing feasibility of linear constraint systems.

Downsampling for Testing and Learning in Product Distributions

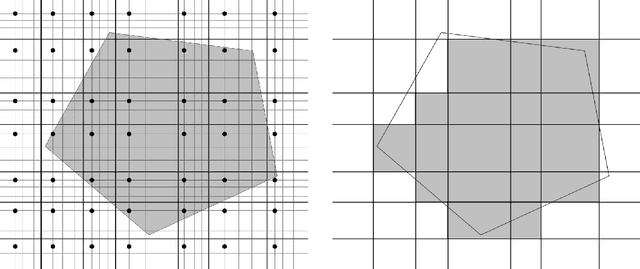
We study the domain reduction problem of eliminating dependence on $n$ from the complexity of property testing and learning algorithms on domain $[n]^d$, and the related problem of establishing testing and learning results for product distributions over $\mathbb{R}^d$. Our method, which we call downsampling, gives conceptually simple proofs for several results: 1. A 1-page proof of the recent $o(d)$-query monotonicity tester for the hypergrid (Black, Chakrabarty & Seshadhri, SODA 2020), and an improvement from $O(d^7)$ to $\widetilde O(d^4)$ in the sample complexity of their distribution-free monotonicity tester for product distributions over $\mathbb{R}^d$; 2. An $\exp(\widetilde O(kd))$-time agnostic learning algorithm for functions of $k$ convex sets in product distributions; 3. A polynomial-time agnostic learning algorithm for functions of a constant number of halfspaces in product distributions; 4. A polynomial-time agnostic learning algorithm for constant-degree polynomial threshold functions in product distributions; 5. An $\exp(\widetilde O(k \sqrt d))$-time agnostic learning algorithm for $k$-alternating functions in product distributions.

Testing Halfspaces over Rotation-Invariant Distributions

We present an algorithm for testing halfspaces over arbitrary, unknown rotation-invariant distributions. Using $\tilde O(\sqrt{n}\epsilon^{-7})$ random examples of an unknown function $f$, the algorithm determines with high probability whether $f$ is of the form $f(x) = sign(\sum_i w_ix_i-t)$ or is $\epsilon$-far from all such functions. This sample size is significantly smaller than the well-known requirement of $\Omega(n)$ samples for learning halfspaces, and known lower bounds imply that our sample size is optimal (in its dependence on $n$) up to logarithmic factors. The algorithm is distribution-free in the sense that it requires no knowledge of the distribution aside from the promise of rotation invariance. To prove the correctness of this algorithm we present a theorem relating the distance between a function and a halfspace to the distance between their centers of mass, that applies to arbitrary distributions.