StepJack: Benchmarking Computer-Use Agent Safety Against Multi-Step Indirect Prompt Injection

Computer-use agents (CUAs) face a growing threat from indirect prompt injection, where adversarial instructions are planted in the environment such as web pages. In this paper, we introduce multi-step indirect prompt injection, a new attack class against CUAs in which the adversarial goal is decomposed into multiple innocuous-looking sub-steps and distributed across a chain of pages referenced along the agent's navigation path. We develop a pipeline to automatically decompose an adversarial goal under the constraint that the execution of the decomposed sub-steps must achieve the original goal while optimizing the innocuousness of each decomposed sub-step. With this pipeline, we build StepJack, a CUA safety benchmark with 480 test examples. On this benchmark, we evaluate six state-of-the-art CUAs and find that at a fixed decomposition depth, multi-step attacks raise attack success rate (ASR) on three of six CUAs, by up to 31.2 points (e.g., GPT-5.4-mini: 41.7% at single-step to 72.9% at three-step); averaged over the five CUAs that can reliably follow the reference chain (all but EvoCUA-32B), ASR rises from 31.3% at single-step to 36.9% at three-step. Dataset and code are available at https://github.com/BorealisAI/StepJack.

Decomposable Submodular Maximization in Federated Setting

Submodular functions, as well as the sub-class of decomposable submodular functions, and their optimization appear in a wide range of applications in machine learning, recommendation systems, and welfare maximization. However, optimization of decomposable submodular functions with millions of component functions is computationally prohibitive. Furthermore, the component functions may be private (they might represent user preference function, for example) and cannot be widely shared. To address these issues, we propose a {\em federated optimization} setting for decomposable submodular optimization. In this setting, clients have their own preference functions, and a weighted sum of these preferences needs to be maximized. We implement the popular {\em continuous greedy} algorithm in this setting where clients take parallel small local steps towards the local solution and then the local changes are aggregated at a central server. To address the large number of clients, the aggregation is performed only on a subsampled set. Further, the aggregation is performed only intermittently between stretches of parallel local steps, which reduces communication cost significantly. We show that our federated algorithm is guaranteed to provide a good approximate solution, even in the presence of above cost-cutting measures. Finally, we show how the federated setting can be incorporated in solving fundamental discrete submodular optimization problems such as Maximum Coverage and Facility Location.

Private Boosted Decision Trees via Smooth Re-Weighting

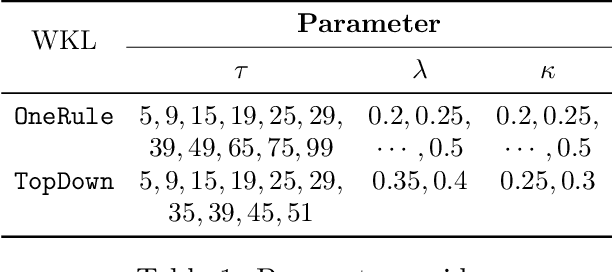
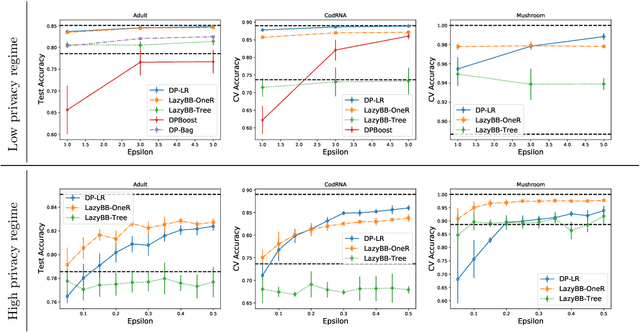
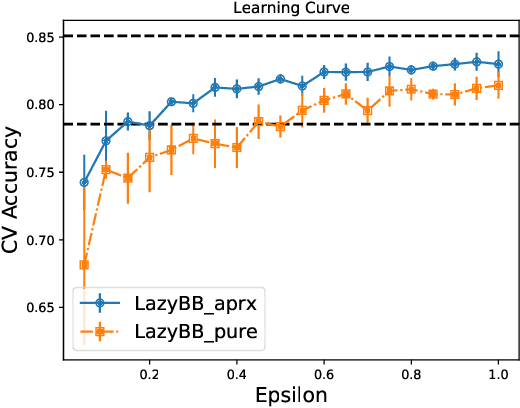
Protecting the privacy of people whose data is used by machine learning algorithms is important. Differential Privacy is the appropriate mathematical framework for formal guarantees of privacy, and boosted decision trees are a popular machine learning technique. So we propose and test a practical algorithm for boosting decision trees that guarantees differential privacy. Privacy is enforced because our booster never puts too much weight on any one example; this ensures that each individual's data never influences a single tree "too much." Experiments show that this boosting algorithm can produce better model sparsity and accuracy than other differentially private ensemble classifiers.

Sparsification of Decomposable Submodular Functions

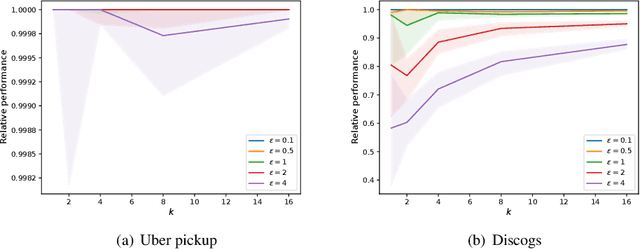
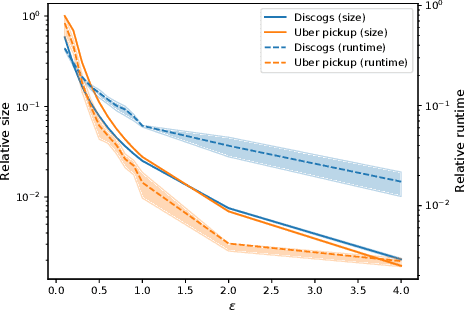
Submodular functions are at the core of many machine learning and data mining tasks. The underlying submodular functions for many of these tasks are decomposable, i.e., they are sum of several simple submodular functions. In many data intensive applications, however, the number of underlying submodular functions in the original function is so large that we need prohibitively large amount of time to process it and/or it does not even fit in the main memory. To overcome this issue, we introduce the notion of sparsification for decomposable submodular functions whose objective is to obtain an accurate approximation of the original function that is a (weighted) sum of only a few submodular functions. Our main result is a polynomial-time randomized sparsification algorithm such that the expected number of functions used in the output is independent of the number of underlying submodular functions in the original function. We also study the effectiveness of our algorithm under various constraints such as matroid and cardinality constraints. We complement our theoretical analysis with an empirical study of the performance of our algorithm.

Fast and Private Submodular and $k$-Submodular Functions Maximization with Matroid Constraints

The problem of maximizing nonnegative monotone submodular functions under a certain constraint has been intensively studied in the last decade, and a wide range of efficient approximation algorithms have been developed for this problem. Many machine learning problems, including data summarization and influence maximization, can be naturally modeled as the problem of maximizing monotone submodular functions. However, when such applications involve sensitive data about individuals, their privacy concerns should be addressed. In this paper, we study the problem of maximizing monotone submodular functions subject to matroid constraints in the framework of differential privacy. We provide $(1-\frac{1}{\mathrm{e}})$-approximation algorithm which improves upon the previous results in terms of approximation guarantee. This is done with an almost cubic number of function evaluations in our algorithm. Moreover, we study $k$-submodularity, a natural generalization of submodularity. We give the first $\frac{1}{2}$-approximation algorithm that preserves differential privacy for maximizing monotone $k$-submodular functions subject to matroid constraints. The approximation ratio is asymptotically tight and is obtained with an almost linear number of function evaluations.