Bahar Salamatian
On the Power of Interactive Proofs for Learning
Apr 11, 2024Abstract:We continue the study of doubly-efficient proof systems for verifying agnostic PAC learning, for which we obtain the following results. - We construct an interactive protocol for learning the $t$ largest Fourier characters of a given function $f \colon \{0,1\}^n \to \{0,1\}$ up to an arbitrarily small error, wherein the verifier uses $\mathsf{poly}(t)$ random examples. This improves upon the Interactive Goldreich-Levin protocol of Goldwasser, Rothblum, Shafer, and Yehudayoff (ITCS 2021) whose sample complexity is $\mathsf{poly}(t,n)$. - For agnostically learning the class $\mathsf{AC}^0[2]$ under the uniform distribution, we build on the work of Carmosino, Impagliazzo, Kabanets, and Kolokolova (APPROX/RANDOM 2017) and design an interactive protocol, where given a function $f \colon \{0,1\}^n \to \{0,1\}$, the verifier learns the closest hypothesis up to $\mathsf{polylog}(n)$ multiplicative factor, using quasi-polynomially many random examples. In contrast, this class has been notoriously resistant even for constructing realisable learners (without a prover) using random examples. - For agnostically learning $k$-juntas under the uniform distribution, we obtain an interactive protocol, where the verifier uses $O(2^k)$ random examples to a given function $f \colon \{0,1\}^n \to \{0,1\}$. Crucially, the sample complexity of the verifier is independent of $n$. We also show that if we do not insist on doubly-efficient proof systems, then the model becomes trivial. Specifically, we show a protocol for an arbitrary class $\mathcal{C}$ of Boolean functions in the distribution-free setting, where the verifier uses $O(1)$ labeled examples to learn $f$.
Private Boosted Decision Trees via Smooth Re-Weighting
Jan 29, 2022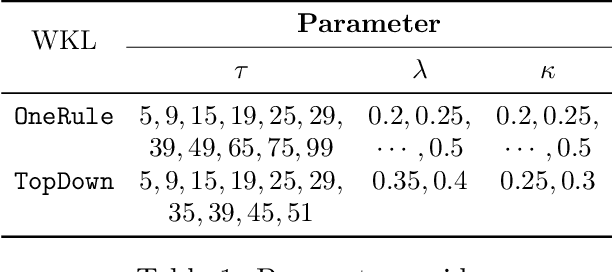
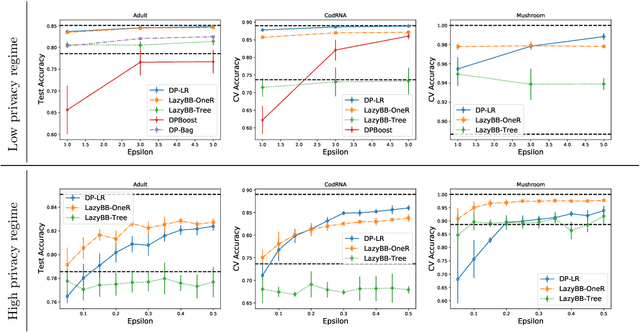
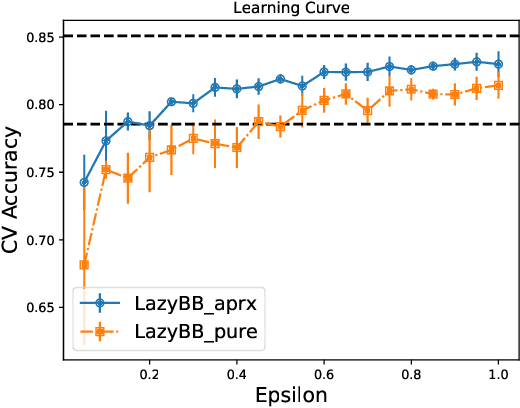
Abstract:Protecting the privacy of people whose data is used by machine learning algorithms is important. Differential Privacy is the appropriate mathematical framework for formal guarantees of privacy, and boosted decision trees are a popular machine learning technique. So we propose and test a practical algorithm for boosting decision trees that guarantees differential privacy. Privacy is enforced because our booster never puts too much weight on any one example; this ensures that each individual's data never influences a single tree "too much." Experiments show that this boosting algorithm can produce better model sparsity and accuracy than other differentially private ensemble classifiers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge