On the Power of Interactive Proofs for Learning

We continue the study of doubly-efficient proof systems for verifying agnostic PAC learning, for which we obtain the following results. - We construct an interactive protocol for learning the $t$ largest Fourier characters of a given function $f \colon \{0,1\}^n \to \{0,1\}$ up to an arbitrarily small error, wherein the verifier uses $\mathsf{poly}(t)$ random examples. This improves upon the Interactive Goldreich-Levin protocol of Goldwasser, Rothblum, Shafer, and Yehudayoff (ITCS 2021) whose sample complexity is $\mathsf{poly}(t,n)$. - For agnostically learning the class $\mathsf{AC}^0[2]$ under the uniform distribution, we build on the work of Carmosino, Impagliazzo, Kabanets, and Kolokolova (APPROX/RANDOM 2017) and design an interactive protocol, where given a function $f \colon \{0,1\}^n \to \{0,1\}$, the verifier learns the closest hypothesis up to $\mathsf{polylog}(n)$ multiplicative factor, using quasi-polynomially many random examples. In contrast, this class has been notoriously resistant even for constructing realisable learners (without a prover) using random examples. - For agnostically learning $k$-juntas under the uniform distribution, we obtain an interactive protocol, where the verifier uses $O(2^k)$ random examples to a given function $f \colon \{0,1\}^n \to \{0,1\}$. Crucially, the sample complexity of the verifier is independent of $n$. We also show that if we do not insist on doubly-efficient proof systems, then the model becomes trivial. Specifically, we show a protocol for an arbitrary class $\mathcal{C}$ of Boolean functions in the distribution-free setting, where the verifier uses $O(1)$ labeled examples to learn $f$.

Information-theoretic generalization bounds for learning from quantum data

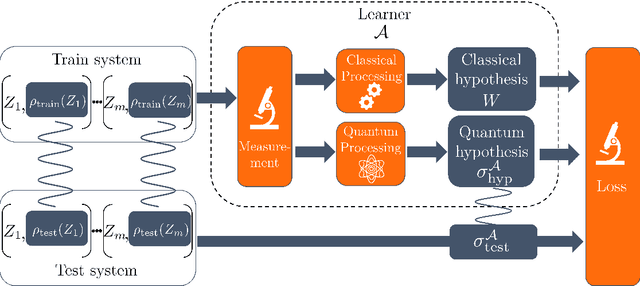
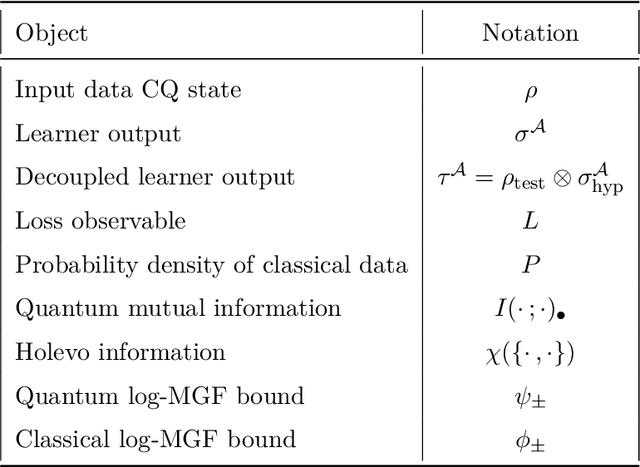
Learning tasks play an increasingly prominent role in quantum information and computation. They range from fundamental problems such as state discrimination and metrology over the framework of quantum probably approximately correct (PAC) learning, to the recently proposed shadow variants of state tomography. However, the many directions of quantum learning theory have so far evolved separately. We propose a general mathematical formalism for describing quantum learning by training on classical-quantum data and then testing how well the learned hypothesis generalizes to new data. In this framework, we prove bounds on the expected generalization error of a quantum learner in terms of classical and quantum information-theoretic quantities measuring how strongly the learner's hypothesis depends on the specific data seen during training. To achieve this, we use tools from quantum optimal transport and quantum concentration inequalities to establish non-commutative versions of decoupling lemmas that underlie recent information-theoretic generalization bounds for classical machine learning. Our framework encompasses and gives intuitively accessible generalization bounds for a variety of quantum learning scenarios such as quantum state discrimination, PAC learning quantum states, quantum parameter estimation, and quantumly PAC learning classical functions. Thereby, our work lays a foundation for a unifying quantum information-theoretic perspective on quantum learning.

Quantum learning algorithms imply circuit lower bounds

We establish the first general connection between the design of quantum algorithms and circuit lower bounds. Specifically, let $\mathfrak{C}$ be a class of polynomial-size concepts, and suppose that $\mathfrak{C}$ can be PAC-learned with membership queries under the uniform distribution with error $1/2 - \gamma$ by a time $T$ quantum algorithm. We prove that if $\gamma^2 \cdot T \ll 2^n/n$, then $\mathsf{BQE} \nsubseteq \mathfrak{C}$, where $\mathsf{BQE} = \mathsf{BQTIME}[2^{O(n)}]$ is an exponential-time analogue of $\mathsf{BQP}$. This result is optimal in both $\gamma$ and $T$, since it is not hard to learn any class $\mathfrak{C}$ of functions in (classical) time $T = 2^n$ (with no error), or in quantum time $T = \mathsf{poly}(n)$ with error at most $1/2 - \Omega(2^{-n/2})$ via Fourier sampling. In other words, even a marginal improvement on these generic learning algorithms would lead to major consequences in complexity theory. Our proof builds on several works in learning theory, pseudorandomness, and computational complexity, and crucially, on a connection between non-trivial classical learning algorithms and circuit lower bounds established by Oliveira and Santhanam (CCC 2017). Extending their approach to quantum learning algorithms turns out to create significant challenges. To achieve that, we show among other results how pseudorandom generators imply learning-to-lower-bound connections in a generic fashion, construct the first conditional pseudorandom generator secure against uniform quantum computations, and extend the local list-decoding algorithm of Impagliazzo, Jaiswal, Kabanets and Wigderson (SICOMP 2010) to quantum circuits via a delicate analysis. We believe that these contributions are of independent interest and might find other applications.

An Adaptivity Hierarchy Theorem for Property Testing

Adaptivity is known to play a crucial role in property testing. In particular, there exist properties for which there is an exponential gap between the power of \emph{adaptive} testing algorithms, wherein each query may be determined by the answers received to prior queries, and their \emph{non-adaptive} counterparts, in which all queries are independent of answers obtained from previous queries. In this work, we investigate the role of adaptivity in property testing at a finer level. We first quantify the degree of adaptivity of a testing algorithm by considering the number of "rounds of adaptivity" it uses. More accurately, we say that a tester is $k$-(round) adaptive if it makes queries in $k+1$ rounds, where the queries in the $i$'th round may depend on the answers obtained in the previous $i-1$ rounds. Then, we ask the following question: Does the power of testing algorithms smoothly grow with the number of rounds of adaptivity? We provide a positive answer to the foregoing question by proving an adaptivity hierarchy theorem for property testing. Specifically, our main result shows that for every $n\in \mathbb{N}$ and $0 \le k \le n^{0.99}$ there exists a property $\mathcal{P}_{n,k}$ of functions for which (1) there exists a $k$-adaptive tester for $\mathcal{P}_{n,k}$ with query complexity $\tilde{O}(k)$, yet (2) any $(k-1)$-adaptive tester for $\mathcal{P}_{n,k}$ must make $\Omega(n)$ queries. In addition, we show that such a qualitative adaptivity hierarchy can be witnessed for testing natural properties of graphs.