Efficient Hamiltonian, structure and trace distance learning of Gaussian states

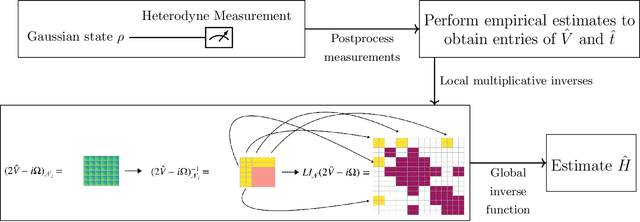
In this work, we initiate the study of Hamiltonian learning for positive temperature bosonic Gaussian states, the quantum generalization of the widely studied problem of learning Gaussian graphical models. We obtain efficient protocols, both in sample and computational complexity, for the task of inferring the parameters of their underlying quadratic Hamiltonian under the assumption of bounded temperature, squeezing, displacement and maximal degree of the interaction graph. Our protocol only requires heterodyne measurements, which are often experimentally feasible, and has a sample complexity that scales logarithmically with the number of modes. Furthermore, we show that it is possible to learn the underlying interaction graph in a similar setting and sample complexity. Taken together, our results put the status of the quantum Hamiltonian learning problem for continuous variable systems in a much more advanced state when compared to spins, where state-of-the-art results are either unavailable or quantitatively inferior to ours. In addition, we use our techniques to obtain the first results on learning Gaussian states in trace distance with a quadratic scaling in precision and polynomial in the number of modes, albeit imposing certain restrictions on the Gaussian states. Our main technical innovations are several continuity bounds for the covariance and Hamiltonian matrix of a Gaussian state, which are of independent interest, combined with what we call the local inversion technique. In essence, the local inversion technique allows us to reliably infer the Hamiltonian of a Gaussian state by only estimating in parallel submatrices of the covariance matrix whose size scales with the desired precision, but not the number of modes. This way we bypass the need to obtain precise global estimates of the covariance matrix, controlling the sample complexity.

Information-theoretic generalization bounds for learning from quantum data

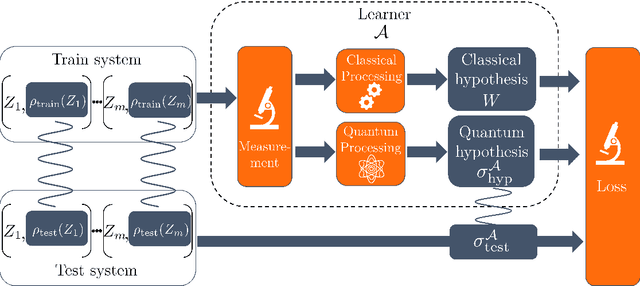
Learning tasks play an increasingly prominent role in quantum information and computation. They range from fundamental problems such as state discrimination and metrology over the framework of quantum probably approximately correct (PAC) learning, to the recently proposed shadow variants of state tomography. However, the many directions of quantum learning theory have so far evolved separately. We propose a general mathematical formalism for describing quantum learning by training on classical-quantum data and then testing how well the learned hypothesis generalizes to new data. In this framework, we prove bounds on the expected generalization error of a quantum learner in terms of classical and quantum information-theoretic quantities measuring how strongly the learner's hypothesis depends on the specific data seen during training. To achieve this, we use tools from quantum optimal transport and quantum concentration inequalities to establish non-commutative versions of decoupling lemmas that underlie recent information-theoretic generalization bounds for classical machine learning. Our framework encompasses and gives intuitively accessible generalization bounds for a variety of quantum learning scenarios such as quantum state discrimination, PAC learning quantum states, quantum parameter estimation, and quantumly PAC learning classical functions. Thereby, our work lays a foundation for a unifying quantum information-theoretic perspective on quantum learning.

Lower Bounds on Learning Pauli Channels

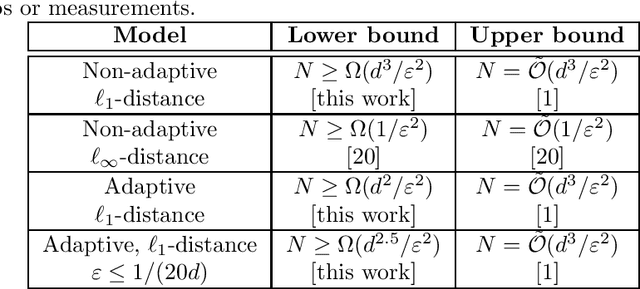
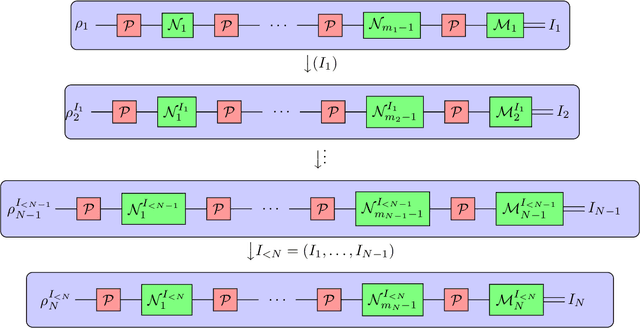
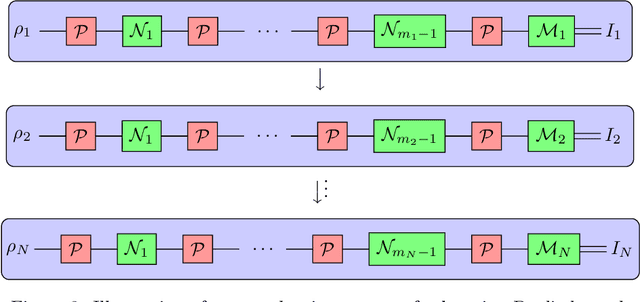
Understanding the noise affecting a quantum device is of fundamental importance for scaling quantum technologies. A particularly important class of noise models is that of Pauli channels, as randomized compiling techniques can effectively bring any quantum channel to this form and are significantly more structured than general quantum channels. In this paper, we show fundamental lower bounds on the sample complexity for learning Pauli channels in diamond norm with unentangled measurements. We consider both adaptive and non-adaptive strategies. In the non-adaptive setting, we show a lower bound of $\Omega(2^{3n}\epsilon^{-2})$ to learn an $n$-qubit Pauli channel. In particular, this shows that the recently introduced learning procedure by Flammia and Wallman is essentially optimal. In the adaptive setting, we show a lower bound of $\Omega(2^{2.5n}\epsilon^{-2})$ for $\epsilon=\mathcal{O}(2^{-n})$, and a lower bound of $\Omega(2^{2n}\epsilon^{-2} )$ for any $\epsilon > 0$. This last lower bound even applies for arbitrarily many sequential uses of the channel, as long as they are only interspersed with other unital operations.

Quantum Differential Privacy: An Information Theory Perspective

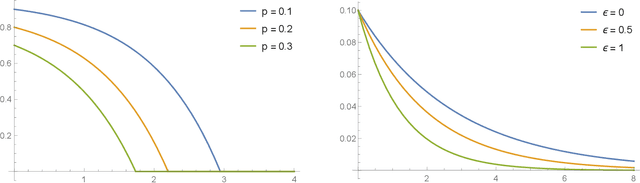
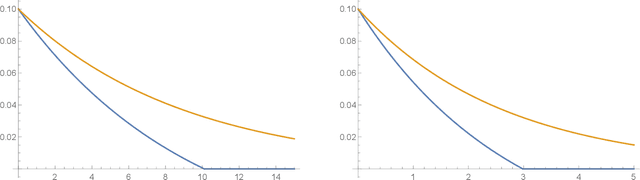
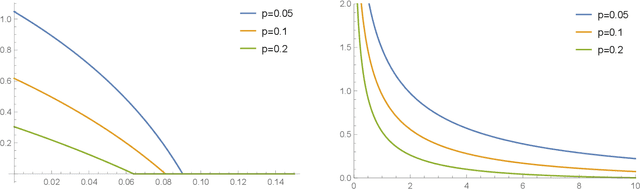
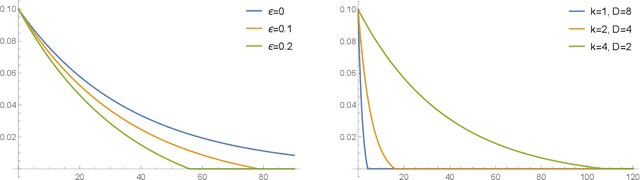
Differential privacy has been an exceptionally successful concept when it comes to providing provable security guarantees for classical computations. More recently, the concept was generalized to quantum computations. While classical computations are essentially noiseless and differential privacy is often achieved by artificially adding noise, near-term quantum computers are inherently noisy and it was observed that this leads to natural differential privacy as a feature. In this work we discuss quantum differential privacy in an information theoretic framework by casting it as a quantum divergence. A main advantage of this approach is that differential privacy becomes a property solely based on the output states of the computation, without the need to check it for every measurement. This leads to simpler proofs and generalized statements of its properties as well as several new bounds for both, general and specific, noise models. In particular, these include common representations of quantum circuits and quantum machine learning concepts. Here, we focus on the difference in the amount of noise required to achieve certain levels of differential privacy versus the amount that would make any computation useless. Finally, we also generalize the classical concepts of local differential privacy, R\'enyi differential privacy and the hypothesis testing interpretation to the quantum setting, providing several new properties and insights.