Convergence of linear programming hierarchies for Gibbs states of spin systems

We consider the problem of computing expectation values of local functions under the Gibbs distribution of a spin system. In particular, we study two families of linear programming hierarchies for this problem. The first hierarchy imposes local spin flip equalities and has been considered in the bootstrap literature in high energy physics. For this hierarchy, we prove fast convergence under a spatial mixing (decay of correlations) condition. This condition is satisfied for example above the critical temperature for Ising models on a $d$-dimensional grid. The second hierarchy is based on a Markov chain having the Gibbs state as a fixed point and has been studied in the optimization literature and more recently in the bootstrap literature. For this hierarchy, we prove fast convergence provided the Markov chain mixes rapidly. Both hierarchies lead to an $\varepsilon$-approximation for local expectation values using a linear program of size quasi-polynomial in $n/\varepsilon$, where $n$ is the total number of sites, provided the interactions can be embedded in a $d$-dimensional grid with constant $d$. Compared to standard Monte Carlo methods, an advantage of this approach is that it always (i.e., for any system) outputs rigorous upper and lower bounds on the expectation value of interest, without needing an a priori analysis of the convergence speed.

Lower Bounds on Learning Pauli Channels

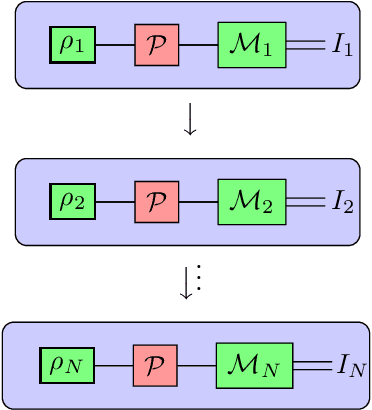
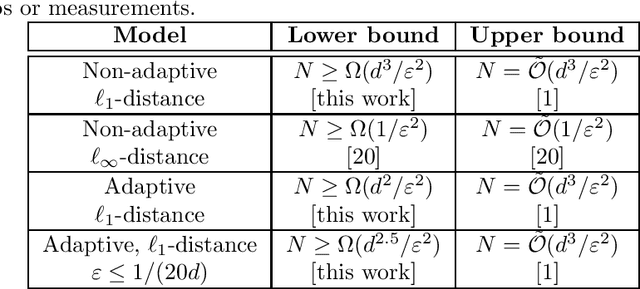
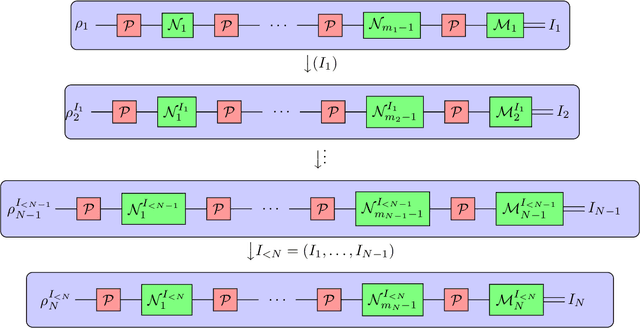
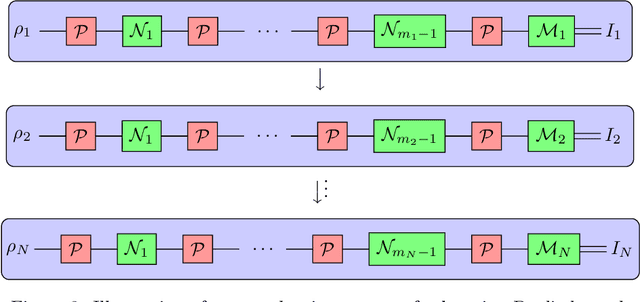
Understanding the noise affecting a quantum device is of fundamental importance for scaling quantum technologies. A particularly important class of noise models is that of Pauli channels, as randomized compiling techniques can effectively bring any quantum channel to this form and are significantly more structured than general quantum channels. In this paper, we show fundamental lower bounds on the sample complexity for learning Pauli channels in diamond norm with unentangled measurements. We consider both adaptive and non-adaptive strategies. In the non-adaptive setting, we show a lower bound of $\Omega(2^{3n}\epsilon^{-2})$ to learn an $n$-qubit Pauli channel. In particular, this shows that the recently introduced learning procedure by Flammia and Wallman is essentially optimal. In the adaptive setting, we show a lower bound of $\Omega(2^{2.5n}\epsilon^{-2})$ for $\epsilon=\mathcal{O}(2^{-n})$, and a lower bound of $\Omega(2^{2n}\epsilon^{-2} )$ for any $\epsilon > 0$. This last lower bound even applies for arbitrarily many sequential uses of the channel, as long as they are only interspersed with other unital operations.

Learning dynamic polynomial proofs

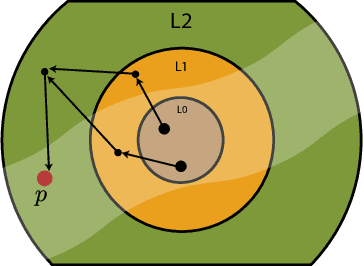
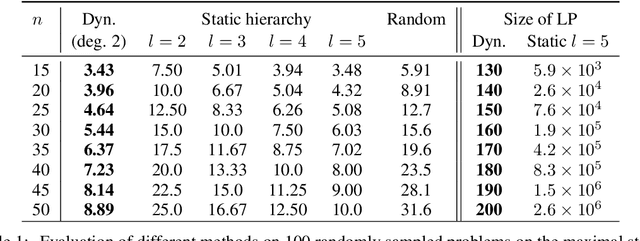
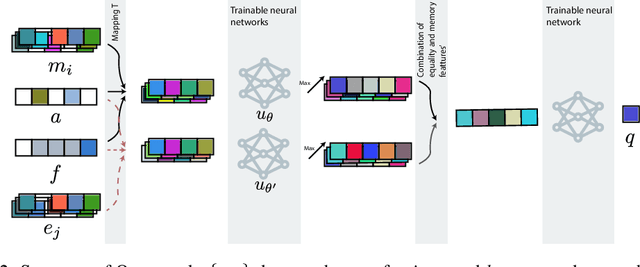
Polynomial inequalities lie at the heart of many mathematical disciplines. In this paper, we consider the fundamental computational task of automatically searching for proofs of polynomial inequalities. We adopt the framework of semi-algebraic proof systems that manipulate polynomial inequalities via elementary inference rules that infer new inequalities from the premises. These proof systems are known to be very powerful, but searching for proofs remains a major difficulty. In this work, we introduce a machine learning based method to search for a dynamic proof within these proof systems. We propose a deep reinforcement learning framework that learns an embedding of the polynomials and guides the choice of inference rules, taking the inherent symmetries of the problem as an inductive bias. We compare our approach with powerful and widely-studied linear programming hierarchies based on static proof systems, and show that our method reduces the size of the linear program by several orders of magnitude while also improving performance. These results hence pave the way towards augmenting powerful and well-studied semi-algebraic proof systems with machine learning guiding strategies for enhancing the expressivity of such proof systems.

Adversarial vulnerability for any classifier

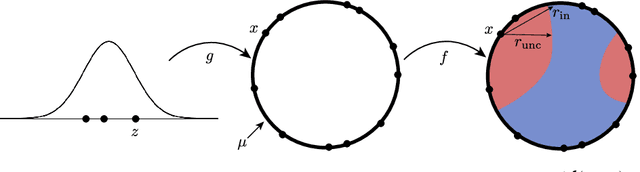
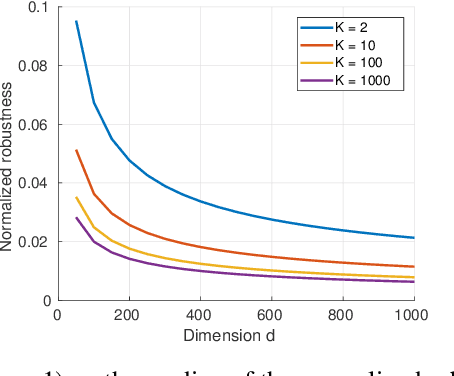
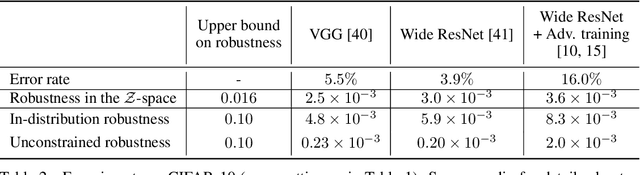
Despite achieving impressive and often superhuman performance on multiple benchmarks, state-of-the-art deep networks remain highly vulnerable to perturbations: adding small, imperceptible, adversarial perturbations can lead to very high error rates. Provided the data distribution is defined using a generative model mapping latent vectors to datapoints in the distribution, we prove that no classifier can be robust to adversarial perturbations when the latent space is sufficiently large and the generative model sufficiently smooth. Under the same conditions, we prove the existence of adversarial perturbations that transfer well across different models with small risk. We conclude the paper with experiments validating the theoretical bounds.

Robustness of classifiers to uniform $\ell\_p$ and Gaussian noise

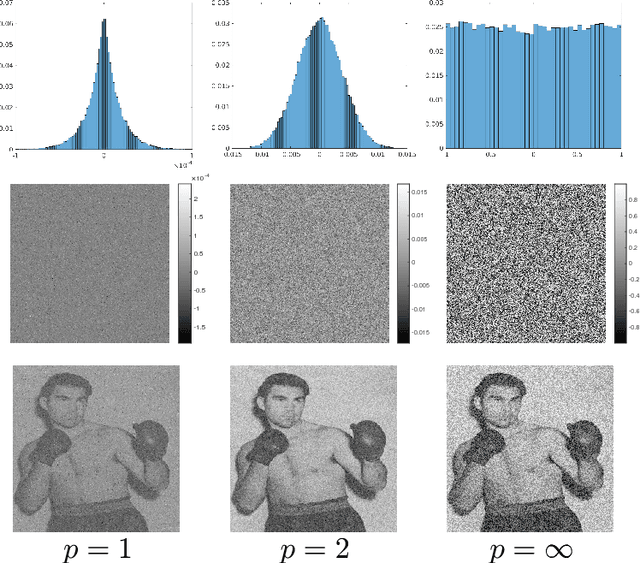
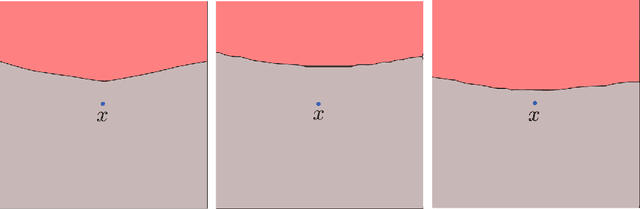
We study the robustness of classifiers to various kinds of random noise models. In particular, we consider noise drawn uniformly from the $\ell\_p$ ball for $p \in [1, \infty]$ and Gaussian noise with an arbitrary covariance matrix. We characterize this robustness to random noise in terms of the distance to the decision boundary of the classifier. This analysis applies to linear classifiers as well as classifiers with locally approximately flat decision boundaries, a condition which is satisfied by state-of-the-art deep neural networks. The predicted robustness is verified experimentally.

Analysis of universal adversarial perturbations

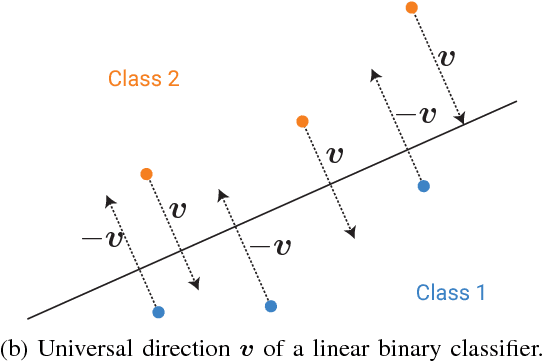
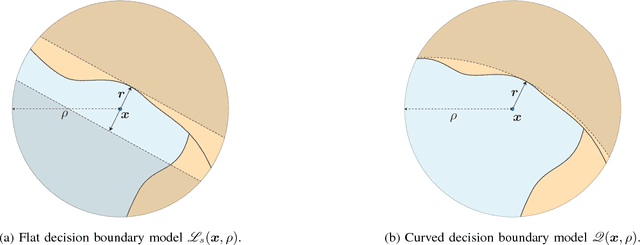
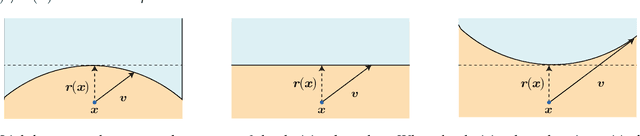
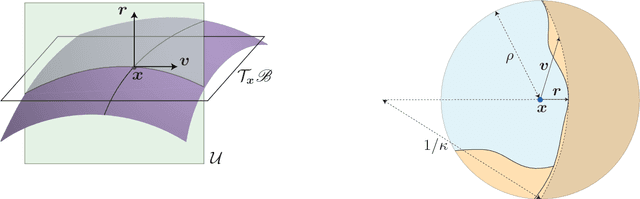
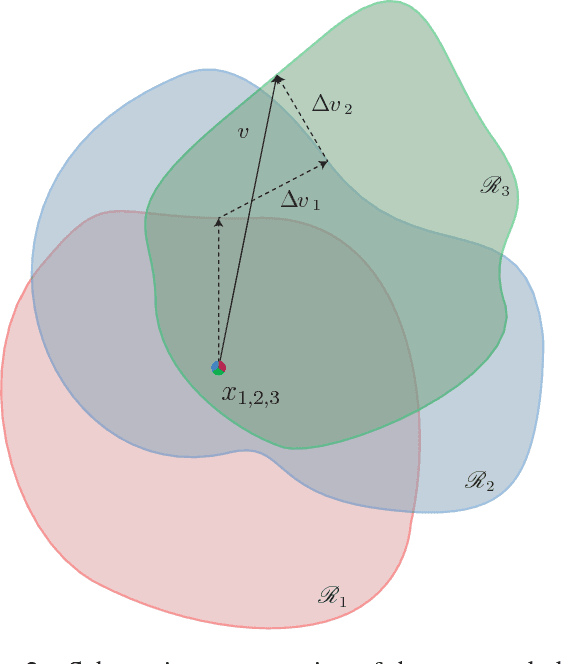
Deep networks have recently been shown to be vulnerable to universal perturbations: there exist very small image-agnostic perturbations that cause most natural images to be misclassified by such classifiers. In this paper, we propose the first quantitative analysis of the robustness of classifiers to universal perturbations, and draw a formal link between the robustness to universal perturbations, and the geometry of the decision boundary. Specifically, we establish theoretical bounds on the robustness of classifiers under two decision boundary models (flat and curved models). We show in particular that the robustness of deep networks to universal perturbations is driven by a key property of their curvature: there exists shared directions along which the decision boundary of deep networks is systematically positively curved. Under such conditions, we prove the existence of small universal perturbations. Our analysis further provides a novel geometric method for computing universal perturbations, in addition to explaining their properties.

Universal adversarial perturbations

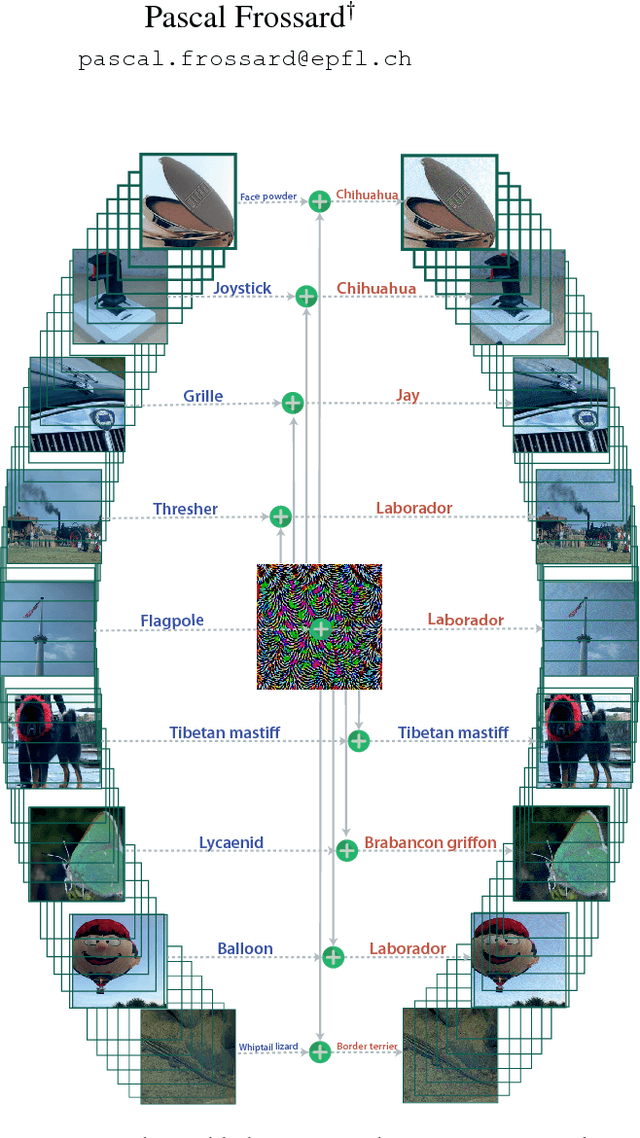
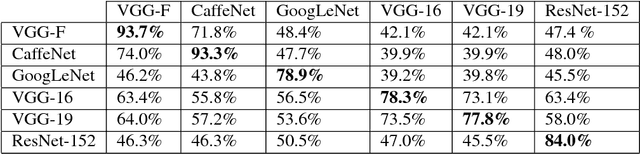
Given a state-of-the-art deep neural network classifier, we show the existence of a universal (image-agnostic) and very small perturbation vector that causes natural images to be misclassified with high probability. We propose a systematic algorithm for computing universal perturbations, and show that state-of-the-art deep neural networks are highly vulnerable to such perturbations, albeit being quasi-imperceptible to the human eye. We further empirically analyze these universal perturbations and show, in particular, that they generalize very well across neural networks. The surprising existence of universal perturbations reveals important geometric correlations among the high-dimensional decision boundary of classifiers. It further outlines potential security breaches with the existence of single directions in the input space that adversaries can possibly exploit to break a classifier on most natural images.

Analysis of classifiers' robustness to adversarial perturbations

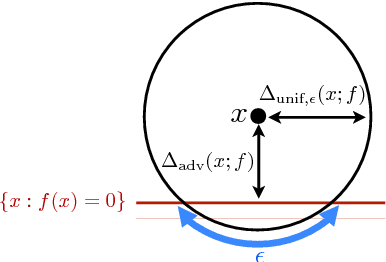
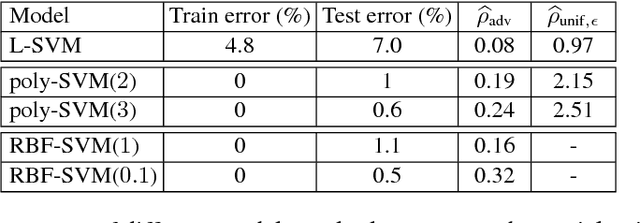
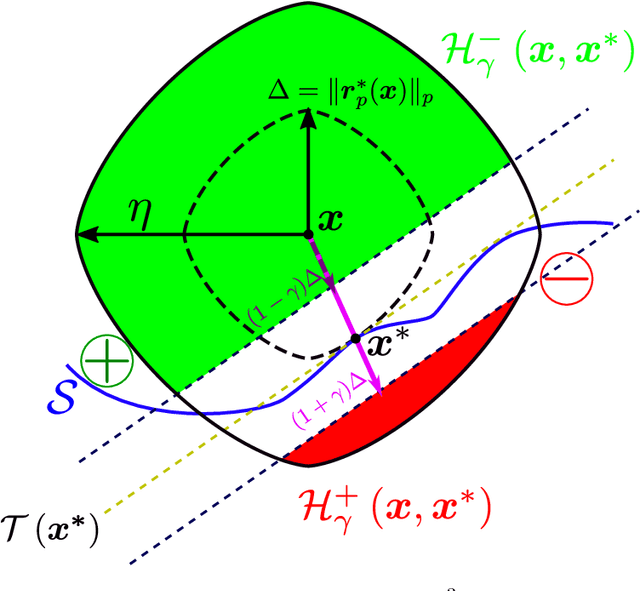
The goal of this paper is to analyze an intriguing phenomenon recently discovered in deep networks, namely their instability to adversarial perturbations (Szegedy et. al., 2014). We provide a theoretical framework for analyzing the robustness of classifiers to adversarial perturbations, and show fundamental upper bounds on the robustness of classifiers. Specifically, we establish a general upper bound on the robustness of classifiers to adversarial perturbations, and then illustrate the obtained upper bound on the families of linear and quadratic classifiers. In both cases, our upper bound depends on a distinguishability measure that captures the notion of difficulty of the classification task. Our results for both classes imply that in tasks involving small distinguishability, no classifier in the considered set will be robust to adversarial perturbations, even if a good accuracy is achieved. Our theoretical framework moreover suggests that the phenomenon of adversarial instability is due to the low flexibility of classifiers, compared to the difficulty of the classification task (captured by the distinguishability). Moreover, we show the existence of a clear distinction between the robustness of a classifier to random noise and its robustness to adversarial perturbations. Specifically, the former is shown to be larger than the latter by a factor that is proportional to \sqrt{d} (with d being the signal dimension) for linear classifiers. This result gives a theoretical explanation for the discrepancy between the two robustness properties in high dimensional problems, which was empirically observed in the context of neural networks. To the best of our knowledge, our results provide the first theoretical work that addresses the phenomenon of adversarial instability recently observed for deep networks. Our analysis is complemented by experimental results on controlled and real-world data.