Quantum Circuit Optimization with AlphaTensor

A key challenge in realizing fault-tolerant quantum computers is circuit optimization. Focusing on the most expensive gates in fault-tolerant quantum computation (namely, the T gates), we address the problem of T-count optimization, i.e., minimizing the number of T gates that are needed to implement a given circuit. To achieve this, we develop AlphaTensor-Quantum, a method based on deep reinforcement learning that exploits the relationship between optimizing T-count and tensor decomposition. Unlike existing methods for T-count optimization, AlphaTensor-Quantum can incorporate domain-specific knowledge about quantum computation and leverage gadgets, which significantly reduces the T-count of the optimized circuits. AlphaTensor-Quantum outperforms the existing methods for T-count optimization on a set of arithmetic benchmarks (even when compared without making use of gadgets). Remarkably, it discovers an efficient algorithm akin to Karatsuba's method for multiplication in finite fields. AlphaTensor-Quantum also finds the best human-designed solutions for relevant arithmetic computations used in Shor's algorithm and for quantum chemistry simulation, thus demonstrating it can save hundreds of hours of research by optimizing relevant quantum circuits in a fully automated way.

Adversarial Robustness through Local Linearization

Adversarial training is an effective methodology for training deep neural networks that are robust against adversarial, norm-bounded perturbations. However, the computational cost of adversarial training grows prohibitively as the size of the model and number of input dimensions increase. Further, training against less expensive and therefore weaker adversaries produces models that are robust against weak attacks but break down under attacks that are stronger. This is often attributed to the phenomenon of gradient obfuscation; such models have a highly non-linear loss surface in the vicinity of training examples, making it hard for gradient-based attacks to succeed even though adversarial examples still exist. In this work, we introduce a novel regularizer that encourages the loss to behave linearly in the vicinity of the training data, thereby penalizing gradient obfuscation while encouraging robustness. We show via extensive experiments on CIFAR-10 and ImageNet, that models trained with our regularizer avoid gradient obfuscation and can be trained significantly faster than adversarial training. Using this regularizer, we exceed current state of the art and achieve 47% adversarial accuracy for ImageNet with l-infinity adversarial perturbations of radius 4/255 under an untargeted, strong, white-box attack. Additionally, we match state of the art results for CIFAR-10 at 8/255.

Learning dynamic polynomial proofs

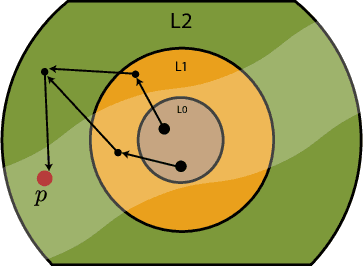
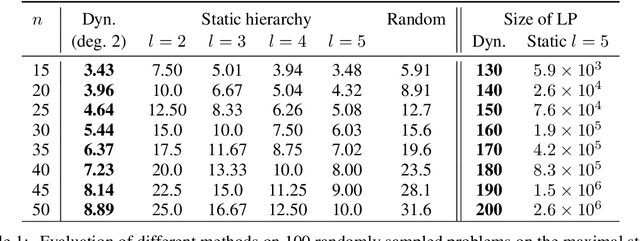
Polynomial inequalities lie at the heart of many mathematical disciplines. In this paper, we consider the fundamental computational task of automatically searching for proofs of polynomial inequalities. We adopt the framework of semi-algebraic proof systems that manipulate polynomial inequalities via elementary inference rules that infer new inequalities from the premises. These proof systems are known to be very powerful, but searching for proofs remains a major difficulty. In this work, we introduce a machine learning based method to search for a dynamic proof within these proof systems. We propose a deep reinforcement learning framework that learns an embedding of the polynomials and guides the choice of inference rules, taking the inherent symmetries of the problem as an inductive bias. We compare our approach with powerful and widely-studied linear programming hierarchies based on static proof systems, and show that our method reduces the size of the linear program by several orders of magnitude while also improving performance. These results hence pave the way towards augmenting powerful and well-studied semi-algebraic proof systems with machine learning guiding strategies for enhancing the expressivity of such proof systems.

Are Labels Required for Improving Adversarial Robustness?

Recent work has uncovered the interesting (and somewhat surprising) finding that training models to be invariant to adversarial perturbations requires substantially larger datasets than those required for standard classification. This result is a key hurdle in the deployment of robust machine learning models in many real world applications where labeled data is expensive. Our main insight is that unlabeled data can be a competitive alternative to labeled data for training adversarially robust models. Theoretically, we show that in a simple statistical setting, the sample complexity for learning an adversarially robust model from unlabeled data matches the fully supervised case up to constant factors. On standard datasets like CIFAR-10, a simple Unsupervised Adversarial Training (UAT) approach using unlabeled data improves robust accuracy by 21.7% over using 4K supervised examples alone, and captures over 95% of the improvement from the same number of labeled examples. Finally, we report an improvement of 4% over the previous state-of-the-art on CIFAR-10 against the strongest known attack by using additional unlabeled data from the uncurated 80 Million Tiny Images dataset. This demonstrates that our finding extends as well to the more realistic case where unlabeled data is also uncurated, therefore opening a new avenue for improving adversarial training.

Verification of deep probabilistic models

Probabilistic models are a critical part of the modern deep learning toolbox - ranging from generative models (VAEs, GANs), sequence to sequence models used in machine translation and speech processing to models over functional spaces (conditional neural processes, neural processes). Given the size and complexity of these models, safely deploying them in applications requires the development of tools to analyze their behavior rigorously and provide some guarantees that these models are consistent with a list of desirable properties or specifications. For example, a machine translation model should produce semantically equivalent outputs for innocuous changes in the input to the model. A functional regression model that is learning a distribution over monotonic functions should predict a larger value at a larger input. Verification of these properties requires a new framework that goes beyond notions of verification studied in deterministic feedforward networks, since requiring worst-case guarantees in probabilistic models is likely to produce conservative or vacuous results. We propose a novel formulation of verification for deep probabilistic models that take in conditioning inputs and sample latent variables in the course of producing an output: We require that the output of the model satisfies a linear constraint with high probability over the sampling of latent variables and for every choice of conditioning input to the model. We show that rigorous lower bounds on the probability that the constraint is satisfied can be obtained efficiently. Experiments with neural processes show that several properties of interest while modeling functional spaces can be modeled within this framework (monotonicity, convexity) and verified efficiently using our algorithms

Robustness via curvature regularization, and vice versa

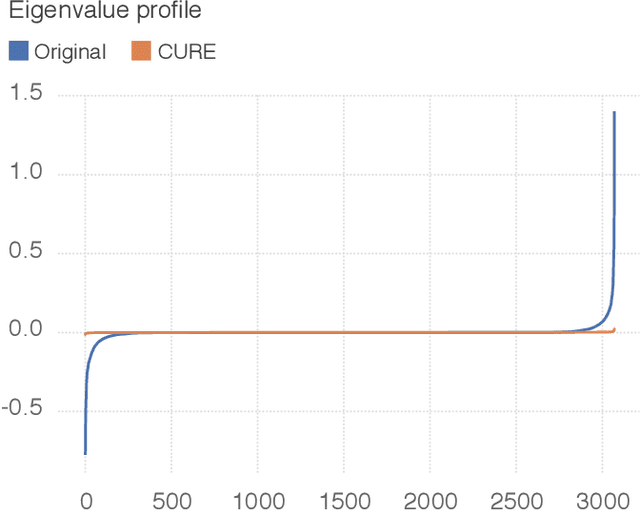
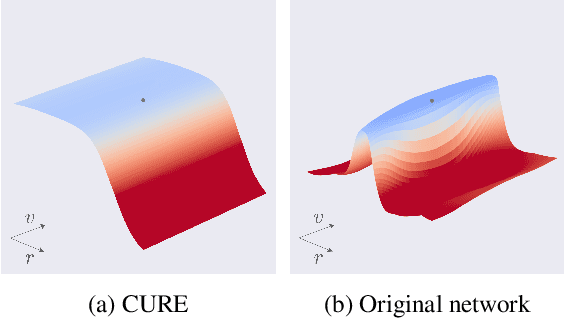
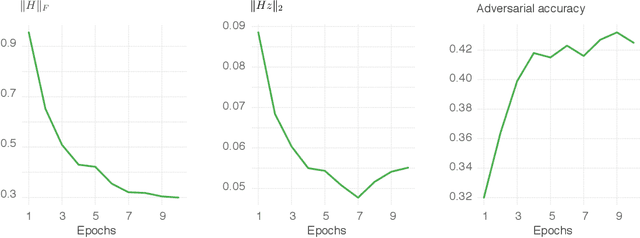
State-of-the-art classifiers have been shown to be largely vulnerable to adversarial perturbations. One of the most effective strategies to improve robustness is adversarial training. In this paper, we investigate the effect of adversarial training on the geometry of the classification landscape and decision boundaries. We show in particular that adversarial training leads to a significant decrease in the curvature of the loss surface with respect to inputs, leading to a drastically more "linear" behaviour of the network. Using a locally quadratic approximation, we provide theoretical evidence on the existence of a strong relation between large robustness and small curvature. To further show the importance of reduced curvature for improving the robustness, we propose a new regularizer that directly minimizes curvature of the loss surface, and leads to adversarial robustness that is on par with adversarial training. Besides being a more efficient and principled alternative to adversarial training, the proposed regularizer confirms our claims on the importance of exhibiting quasi-linear behavior in the vicinity of data points in order to achieve robustness.

SaaS: Speed as a Supervisor for Semi-supervised Learning

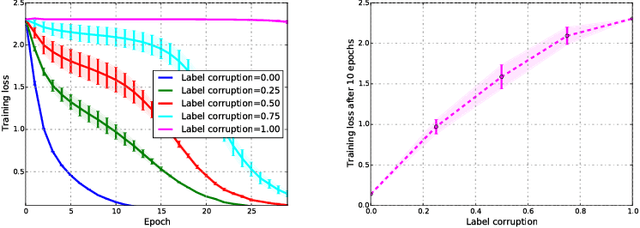
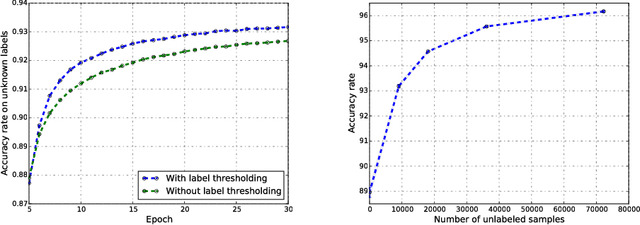
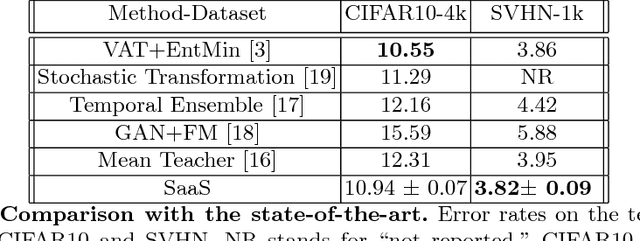
We introduce the SaaS Algorithm for semi-supervised learning, which uses learning speed during stochastic gradient descent in a deep neural network to measure the quality of an iterative estimate of the posterior probability of unknown labels. Training speed in supervised learning correlates strongly with the percentage of correct labels, so we use it as an inference criterion for the unknown labels, without attempting to infer the model parameters at first. Despite its simplicity, SaaS achieves state-of-the-art results in semi-supervised learning benchmarks.

Adversarial vulnerability for any classifier

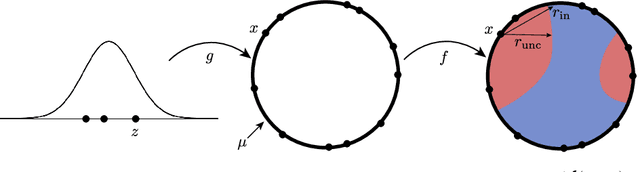
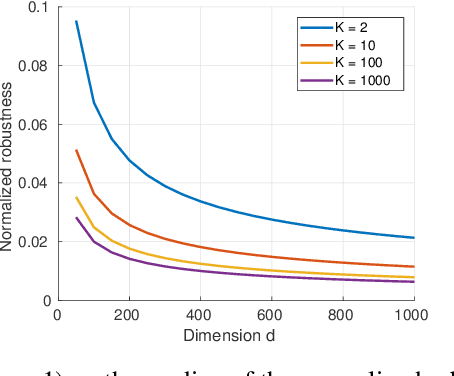
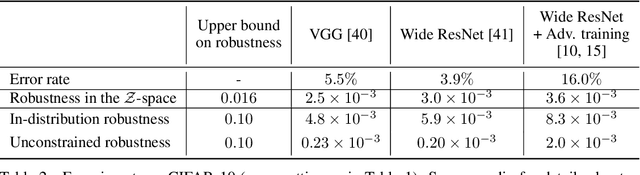
Despite achieving impressive and often superhuman performance on multiple benchmarks, state-of-the-art deep networks remain highly vulnerable to perturbations: adding small, imperceptible, adversarial perturbations can lead to very high error rates. Provided the data distribution is defined using a generative model mapping latent vectors to datapoints in the distribution, we prove that no classifier can be robust to adversarial perturbations when the latent space is sufficiently large and the generative model sufficiently smooth. Under the same conditions, we prove the existence of adversarial perturbations that transfer well across different models with small risk. We conclude the paper with experiments validating the theoretical bounds.

Robustness of classifiers to uniform $\ell\_p$ and Gaussian noise

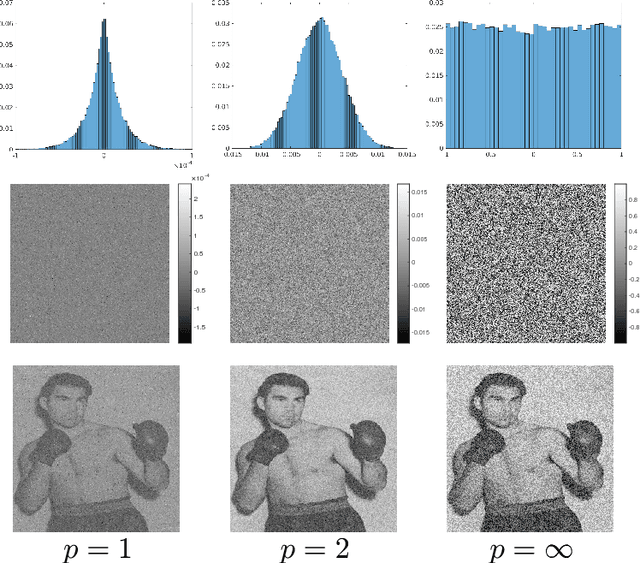
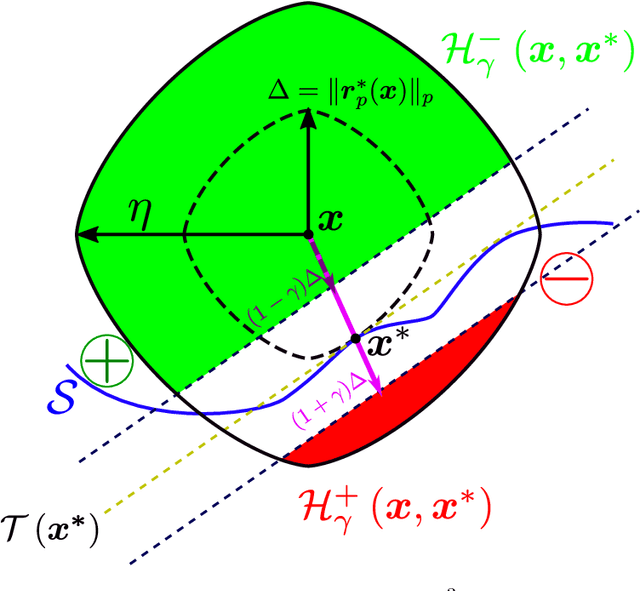
We study the robustness of classifiers to various kinds of random noise models. In particular, we consider noise drawn uniformly from the $\ell\_p$ ball for $p \in [1, \infty]$ and Gaussian noise with an arbitrary covariance matrix. We characterize this robustness to random noise in terms of the distance to the decision boundary of the classifier. This analysis applies to linear classifiers as well as classifiers with locally approximately flat decision boundaries, a condition which is satisfied by state-of-the-art deep neural networks. The predicted robustness is verified experimentally.

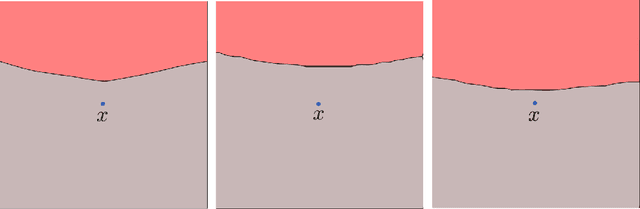
Analysis of universal adversarial perturbations

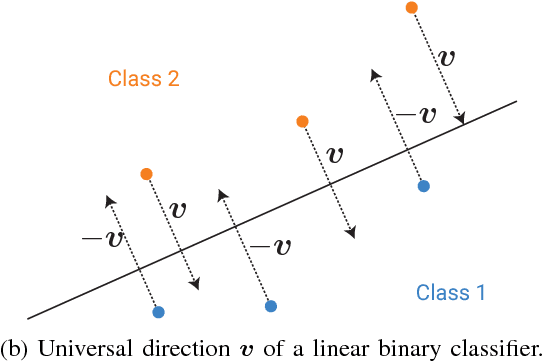
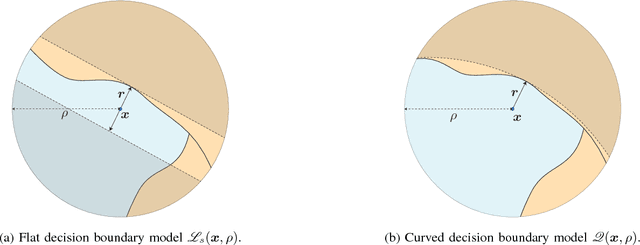
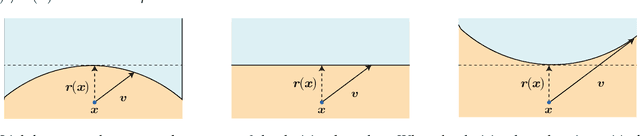
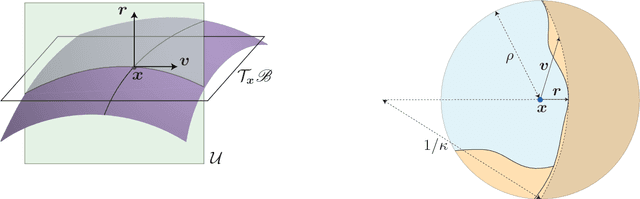
Deep networks have recently been shown to be vulnerable to universal perturbations: there exist very small image-agnostic perturbations that cause most natural images to be misclassified by such classifiers. In this paper, we propose the first quantitative analysis of the robustness of classifiers to universal perturbations, and draw a formal link between the robustness to universal perturbations, and the geometry of the decision boundary. Specifically, we establish theoretical bounds on the robustness of classifiers under two decision boundary models (flat and curved models). We show in particular that the robustness of deep networks to universal perturbations is driven by a key property of their curvature: there exists shared directions along which the decision boundary of deep networks is systematically positively curved. Under such conditions, we prove the existence of small universal perturbations. Our analysis further provides a novel geometric method for computing universal perturbations, in addition to explaining their properties.