Normalization and effective learning rates in reinforcement learning

Normalization layers have recently experienced a renaissance in the deep reinforcement learning and continual learning literature, with several works highlighting diverse benefits such as improving loss landscape conditioning and combatting overestimation bias. However, normalization brings with it a subtle but important side effect: an equivalence between growth in the norm of the network parameters and decay in the effective learning rate. This becomes problematic in continual learning settings, where the resulting effective learning rate schedule may decay to near zero too quickly relative to the timescale of the learning problem. We propose to make the learning rate schedule explicit with a simple re-parameterization which we call Normalize-and-Project (NaP), which couples the insertion of normalization layers with weight projection, ensuring that the effective learning rate remains constant throughout training. This technique reveals itself as a powerful analytical tool to better understand learning rate schedules in deep reinforcement learning, and as a means of improving robustness to nonstationarity in synthetic plasticity loss benchmarks along with both the single-task and sequential variants of the Arcade Learning Environment. We also show that our approach can be easily applied to popular architectures such as ResNets and transformers while recovering and in some cases even slightly improving the performance of the base model in common stationary benchmarks.

Disentangling the Causes of Plasticity Loss in Neural Networks

Underpinning the past decades of work on the design, initialization, and optimization of neural networks is a seemingly innocuous assumption: that the network is trained on a \textit{stationary} data distribution. In settings where this assumption is violated, e.g.\ deep reinforcement learning, learning algorithms become unstable and brittle with respect to hyperparameters and even random seeds. One factor driving this instability is the loss of plasticity, meaning that updating the network's predictions in response to new information becomes more difficult as training progresses. While many recent works provide analyses and partial solutions to this phenomenon, a fundamental question remains unanswered: to what extent do known mechanisms of plasticity loss overlap, and how can mitigation strategies be combined to best maintain the trainability of a network? This paper addresses these questions, showing that loss of plasticity can be decomposed into multiple independent mechanisms and that, while intervening on any single mechanism is insufficient to avoid the loss of plasticity in all cases, intervening on multiple mechanisms in conjunction results in highly robust learning algorithms. We show that a combination of layer normalization and weight decay is highly effective at maintaining plasticity in a variety of synthetic nonstationary learning tasks, and further demonstrate its effectiveness on naturally arising nonstationarities, including reinforcement learning in the Arcade Learning Environment.

Deep Transformers without Shortcuts: Modifying Self-attention for Faithful Signal Propagation

Skip connections and normalisation layers form two standard architectural components that are ubiquitous for the training of Deep Neural Networks (DNNs), but whose precise roles are poorly understood. Recent approaches such as Deep Kernel Shaping have made progress towards reducing our reliance on them, using insights from wide NN kernel theory to improve signal propagation in vanilla DNNs (which we define as networks without skips or normalisation). However, these approaches are incompatible with the self-attention layers present in transformers, whose kernels are intrinsically more complicated to analyse and control. And so the question remains: is it possible to train deep vanilla transformers? We answer this question in the affirmative by designing several approaches that use combinations of parameter initialisations, bias matrices and location-dependent rescaling to achieve faithful signal propagation in vanilla transformers. Our methods address various intricacies specific to signal propagation in transformers, including the interaction with positional encoding and causal masking. In experiments on WikiText-103 and C4, our approaches enable deep transformers without normalisation to train at speeds matching their standard counterparts, and deep vanilla transformers to reach the same performance as standard ones after about 5 times more iterations.

Pre-training via Denoising for Molecular Property Prediction

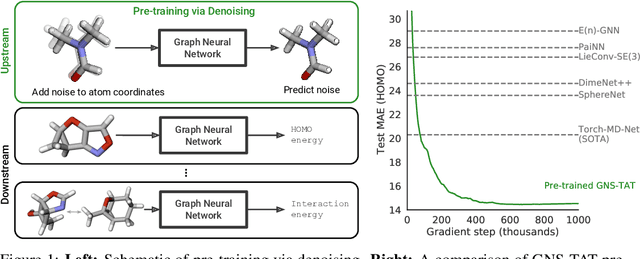
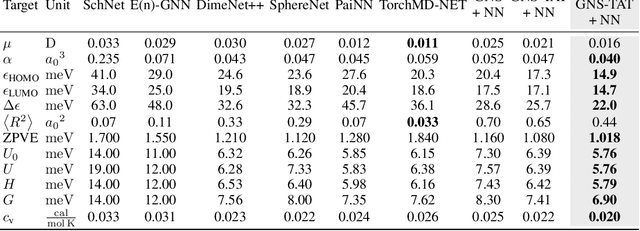
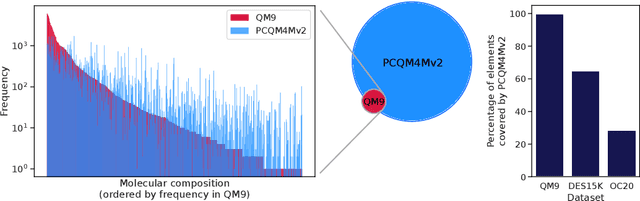
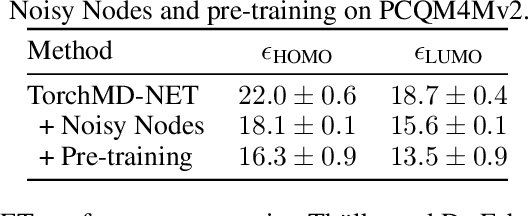
Many important problems involving molecular property prediction from 3D structures have limited data, posing a generalization challenge for neural networks. In this paper, we describe a pre-training technique that utilizes large datasets of 3D molecular structures at equilibrium to learn meaningful representations for downstream tasks. Inspired by recent advances in noise regularization, our pre-training objective is based on denoising. Relying on the well-known link between denoising autoencoders and score-matching, we also show that the objective corresponds to learning a molecular force field -- arising from approximating the physical state distribution with a mixture of Gaussians -- directly from equilibrium structures. Our experiments demonstrate that using this pre-training objective significantly improves performance on multiple benchmarks, achieving a new state-of-the-art on the majority of targets in the widely used QM9 dataset. Our analysis then provides practical insights into the effects of different factors -- dataset sizes, model size and architecture, and the choice of upstream and downstream datasets -- on pre-training.

Deep Learning without Shortcuts: Shaping the Kernel with Tailored Rectifiers

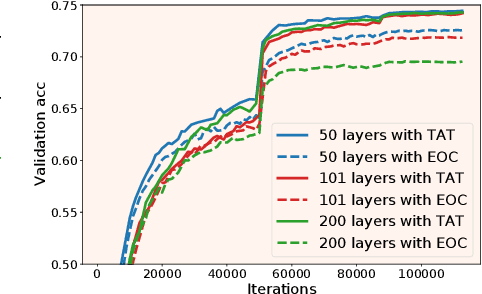
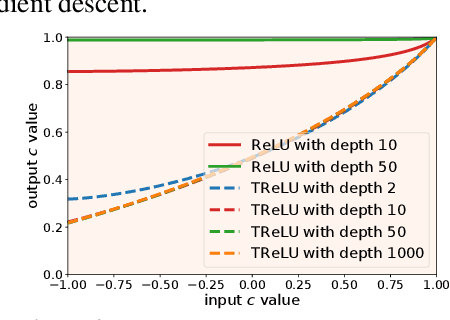
Training very deep neural networks is still an extremely challenging task. The common solution is to use shortcut connections and normalization layers, which are both crucial ingredients in the popular ResNet architecture. However, there is strong evidence to suggest that ResNets behave more like ensembles of shallower networks than truly deep ones. Recently, it was shown that deep vanilla networks (i.e. networks without normalization layers or shortcut connections) can be trained as fast as ResNets by applying certain transformations to their activation functions. However, this method (called Deep Kernel Shaping) isn't fully compatible with ReLUs, and produces networks that overfit significantly more than ResNets on ImageNet. In this work, we rectify this situation by developing a new type of transformation that is fully compatible with a variant of ReLUs -- Leaky ReLUs. We show in experiments that our method, which introduces negligible extra computational cost, achieves validation accuracies with deep vanilla networks that are competitive with ResNets (of the same width/depth), and significantly higher than those obtained with the Edge of Chaos (EOC) method. And unlike with EOC, the validation accuracies we obtain do not get worse with depth.

Rapid training of deep neural networks without skip connections or normalization layers using Deep Kernel Shaping

Using an extended and formalized version of the Q/C map analysis of Poole et al. (2016), along with Neural Tangent Kernel theory, we identify the main pathologies present in deep networks that prevent them from training fast and generalizing to unseen data, and show how these can be avoided by carefully controlling the "shape" of the network's initialization-time kernel function. We then develop a method called Deep Kernel Shaping (DKS), which accomplishes this using a combination of precise parameter initialization, activation function transformations, and small architectural tweaks, all of which preserve the model class. In our experiments we show that DKS enables SGD training of residual networks without normalization layers on Imagenet and CIFAR-10 classification tasks at speeds comparable to standard ResNetV2 and Wide-ResNet models, with only a small decrease in generalization performance. And when using K-FAC as the optimizer, we achieve similar results for networks without skip connections. Our results apply for a large variety of activation functions, including those which traditionally perform very badly, such as the logistic sigmoid. In addition to DKS, we contribute a detailed analysis of skip connections, normalization layers, special activation functions like RELU and SELU, and various initialization schemes, explaining their effectiveness as alternative (and ultimately incomplete) ways of "shaping" the network's initialization-time kernel.

On the validity of kernel approximations for orthogonally-initialized neural networks

In this note we extend kernel function approximation results for neural networks with Gaussian-distributed weights to single-layer networks initialized using Haar-distributed random orthogonal matrices (with possible rescaling). This is accomplished using recent results from random matrix theory.

Which Algorithmic Choices Matter at Which Batch Sizes? Insights From a Noisy Quadratic Model

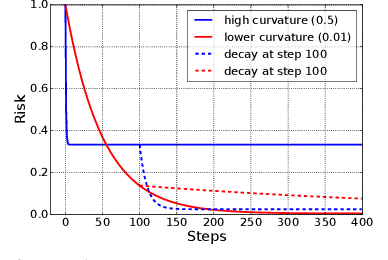
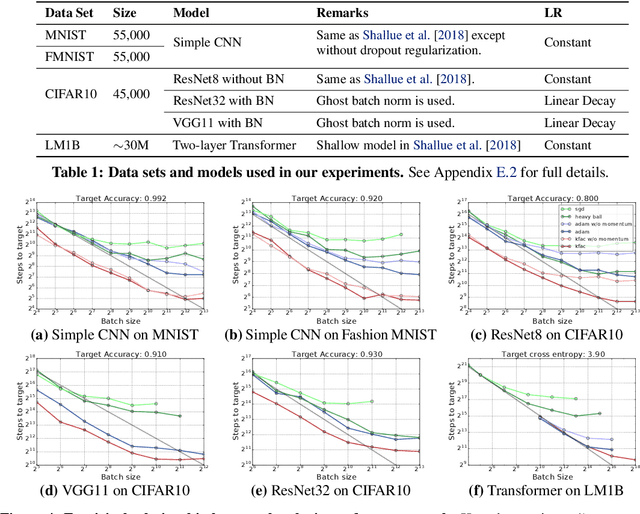
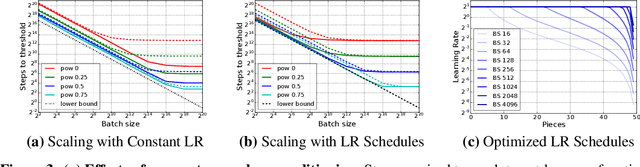
Increasing the batch size is a popular way to speed up neural network training, but beyond some critical batch size, larger batch sizes yield diminishing returns. In this work, we study how the critical batch size changes based on properties of the optimization algorithm, including acceleration and preconditioning, through two different lenses: large scale experiments, and analysis of a simple noisy quadratic model (NQM). We experimentally demonstrate that optimization algorithms that employ preconditioning, specifically Adam and K-FAC, result in much larger critical batch sizes than stochastic gradient descent with momentum. We also demonstrate that the NQM captures many of the essential features of real neural network training, despite being drastically simpler to work with. The NQM predicts our results with preconditioned optimizers, previous results with accelerated gradient descent, and other results around optimal learning rates and large batch training, making it a useful tool to generate testable predictions about neural network optimization.

Adversarial Robustness through Local Linearization

Adversarial training is an effective methodology for training deep neural networks that are robust against adversarial, norm-bounded perturbations. However, the computational cost of adversarial training grows prohibitively as the size of the model and number of input dimensions increase. Further, training against less expensive and therefore weaker adversaries produces models that are robust against weak attacks but break down under attacks that are stronger. This is often attributed to the phenomenon of gradient obfuscation; such models have a highly non-linear loss surface in the vicinity of training examples, making it hard for gradient-based attacks to succeed even though adversarial examples still exist. In this work, we introduce a novel regularizer that encourages the loss to behave linearly in the vicinity of the training data, thereby penalizing gradient obfuscation while encouraging robustness. We show via extensive experiments on CIFAR-10 and ImageNet, that models trained with our regularizer avoid gradient obfuscation and can be trained significantly faster than adversarial training. Using this regularizer, we exceed current state of the art and achieve 47% adversarial accuracy for ImageNet with l-infinity adversarial perturbations of radius 4/255 under an untargeted, strong, white-box attack. Additionally, we match state of the art results for CIFAR-10 at 8/255.

Fast Convergence of Natural Gradient Descent for Overparameterized Neural Networks

Natural gradient descent has proven effective at mitigating the effects of pathological curvature in neural network optimization, but little is known theoretically about its convergence properties, especially for \emph{nonlinear} networks. In this work, we analyze \emph{for the first time} the speed of convergence for natural gradient descent on nonlinear neural networks with the squared-error loss. We identify two conditions which guarantee the efficient convergence from random initializations: (1) the Jacobian matrix (of network's output for all training cases with respect to the parameters) is full row rank, and (2) the Jacobian matrix is stable for small perturbations around the initialization. For two-layer ReLU neural networks (i.e., with one hidden layer), we prove that these two conditions do in fact hold throughout the training, under the assumptions of nondegenerate inputs and overparameterization. We further extend our analysis to more general loss functions. Lastly, we show that K-FAC, an approximate natural gradient descent method, also converges to global minima under the same assumptions.