Christopher J. Shallue
A Large Batch Optimizer Reality Check: Traditional, Generic Optimizers Suffice Across Batch Sizes
Feb 16, 2021



Abstract:Recently the LARS and LAMB optimizers have been proposed for training neural networks faster using large batch sizes. LARS and LAMB add layer-wise normalization to the update rules of Heavy-ball momentum and Adam, respectively, and have become popular in prominent benchmarks and deep learning libraries. However, without fair comparisons to standard optimizers, it remains an open question whether LARS and LAMB have any benefit over traditional, generic algorithms. In this work we demonstrate that standard optimization algorithms such as Nesterov momentum and Adam can match or exceed the results of LARS and LAMB at large batch sizes. Our results establish new, stronger baselines for future comparisons at these batch sizes and shed light on the difficulties of comparing optimizers for neural network training more generally.
Identifying Exoplanets with Deep Learning. IV. Removing Stellar Activity Signals from Radial Velocity Measurements Using Neural Networks
Nov 04, 2020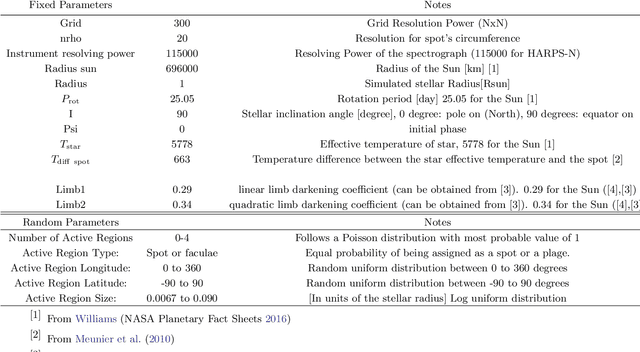
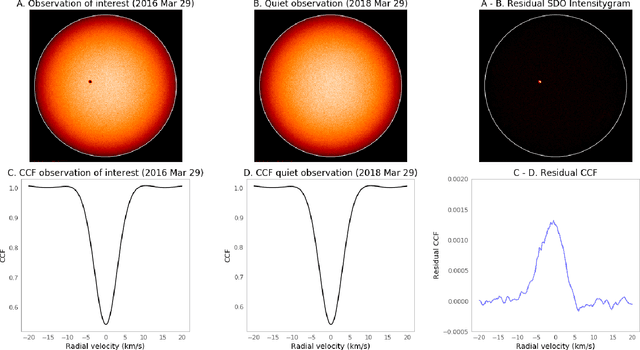
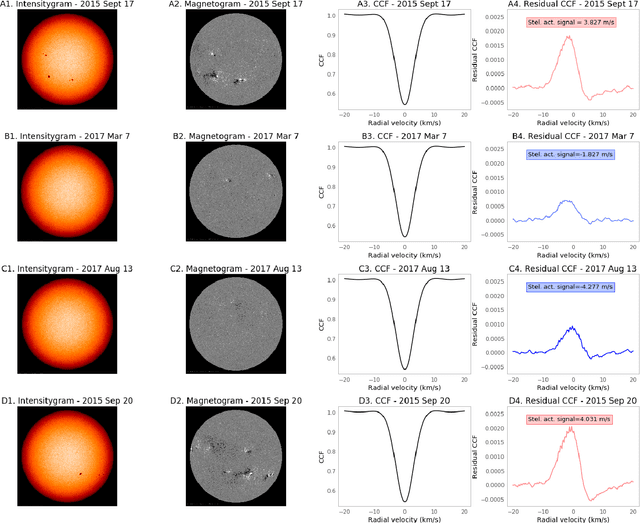
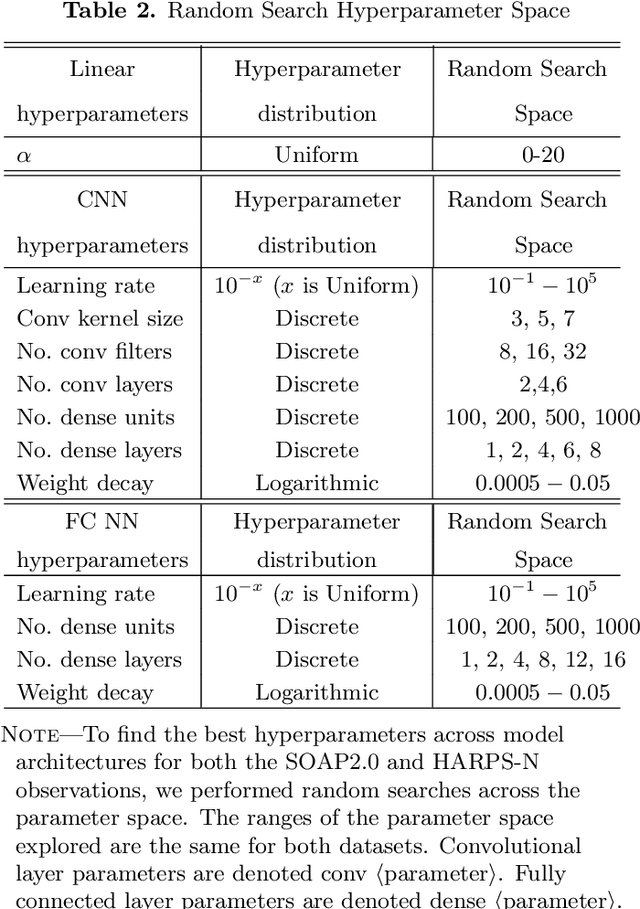
Abstract:Exoplanet detection with precise radial velocity (RV) observations is currently limited by spurious RV signals introduced by stellar activity. We show that machine learning techniques such as linear regression and neural networks can effectively remove the activity signals (due to starspots/faculae) from RV observations. Previous efforts focused on carefully filtering out activity signals in time using modeling techniques like Gaussian Process regression (e.g. Haywood et al. 2014). Instead, we systematically remove activity signals using only changes to the average shape of spectral lines, and no information about when the observations were collected. We trained our machine learning models on both simulated data (generated with the SOAP 2.0 software; Dumusque et al. 2014) and observations of the Sun from the HARPS-N Solar Telescope (Dumusque et al. 2015; Phillips et al. 2016; Collier Cameron et al. 2019). We find that these techniques can predict and remove stellar activity from both simulated data (improving RV scatter from 82 cm/s to 3 cm/s) and from more than 600 real observations taken nearly daily over three years with the HARPS-N Solar Telescope (improving the RV scatter from 1.47 m/s to 0.78 m/s, a factor of ~ 1.9 improvement). In the future, these or similar techniques could remove activity signals from observations of stars outside our solar system and eventually help detect habitable-zone Earth-mass exoplanets around Sun-like stars.
On Empirical Comparisons of Optimizers for Deep Learning
Oct 11, 2019



Abstract:Selecting an optimizer is a central step in the contemporary deep learning pipeline. In this paper, we demonstrate the sensitivity of optimizer comparisons to the metaparameter tuning protocol. Our findings suggest that the metaparameter search space may be the single most important factor explaining the rankings obtained by recent empirical comparisons in the literature. In fact, we show that these results can be contradicted when metaparameter search spaces are changed. As tuning effort grows without bound, more general optimizers should never underperform the ones they can approximate (i.e., Adam should never perform worse than momentum), but recent attempts to compare optimizers either assume these inclusion relationships are not practically relevant or restrict the metaparameters in ways that break the inclusions. In our experiments, we find that inclusion relationships between optimizers matter in practice and always predict optimizer comparisons. In particular, we find that the popular adaptive gradient methods never underperform momentum or gradient descent. We also report practical tips around tuning often ignored metaparameters of adaptive gradient methods and raise concerns about fairly benchmarking optimizers for neural network training.
Faster Neural Network Training with Data Echoing
Jul 12, 2019



Abstract:In the twilight of Moore's law, GPUs and other specialized hardware accelerators have dramatically sped up neural network training. However, earlier stages of the training pipeline, such as disk I/O and data preprocessing, do not run on accelerators. As accelerators continue to improve, these earlier stages will increasingly become the bottleneck. In this paper, we introduce "data echoing," which reduces the total computation used by earlier pipeline stages and speeds up training whenever computation upstream from accelerators dominates the training time. Data echoing reuses (or "echoes") intermediate outputs from earlier pipeline stages in order to reclaim idle capacity. We investigate the behavior of different data echoing algorithms on various workloads, for various amounts of echoing, and for various batch sizes. We find that in all settings, at least one data echoing algorithm can match the baseline's predictive performance using less upstream computation. In some cases, data echoing can even compensate for a 4x slower input pipeline.
Which Algorithmic Choices Matter at Which Batch Sizes? Insights From a Noisy Quadratic Model
Jul 09, 2019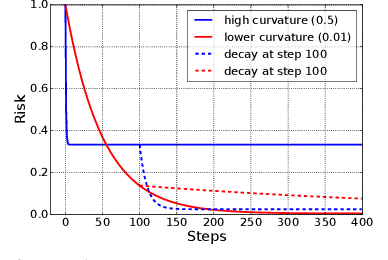
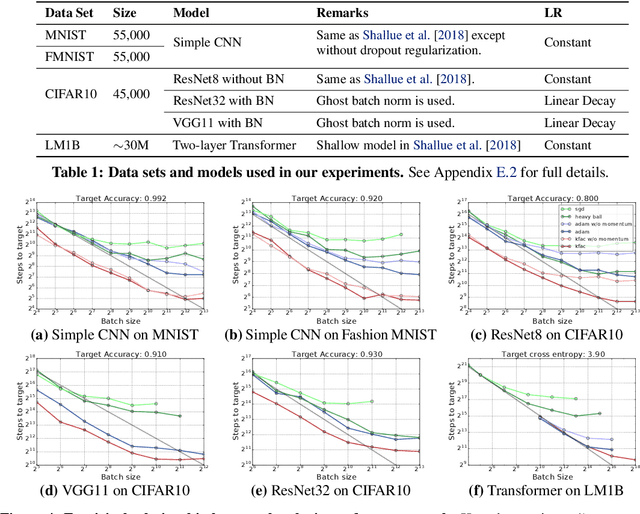
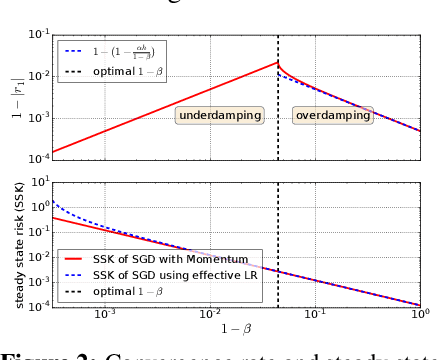
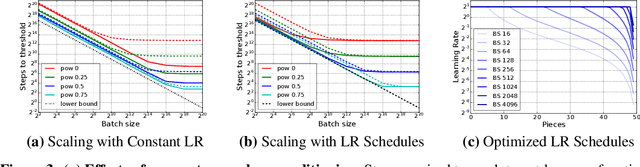
Abstract:Increasing the batch size is a popular way to speed up neural network training, but beyond some critical batch size, larger batch sizes yield diminishing returns. In this work, we study how the critical batch size changes based on properties of the optimization algorithm, including acceleration and preconditioning, through two different lenses: large scale experiments, and analysis of a simple noisy quadratic model (NQM). We experimentally demonstrate that optimization algorithms that employ preconditioning, specifically Adam and K-FAC, result in much larger critical batch sizes than stochastic gradient descent with momentum. We also demonstrate that the NQM captures many of the essential features of real neural network training, despite being drastically simpler to work with. The NQM predicts our results with preconditioned optimizers, previous results with accelerated gradient descent, and other results around optimal learning rates and large batch training, making it a useful tool to generate testable predictions about neural network optimization.
Measuring the Effects of Data Parallelism on Neural Network Training
Nov 21, 2018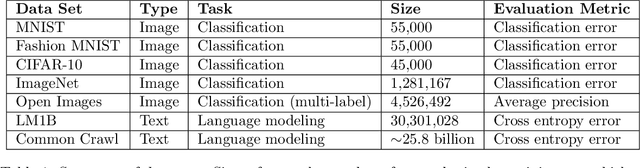
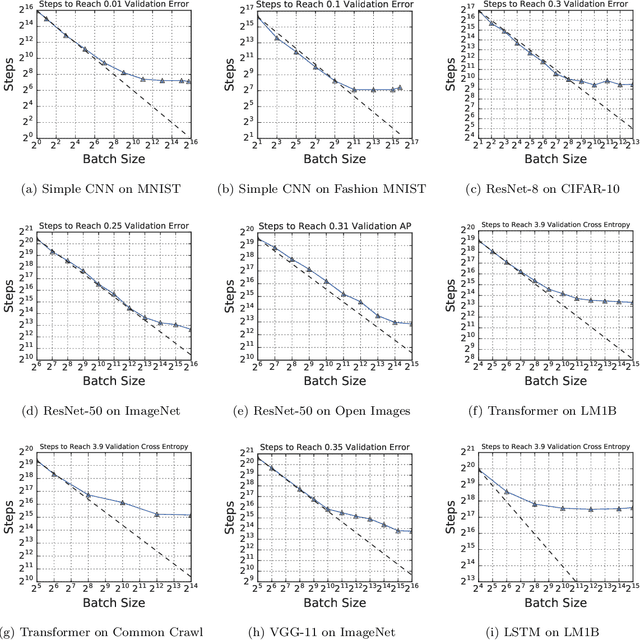
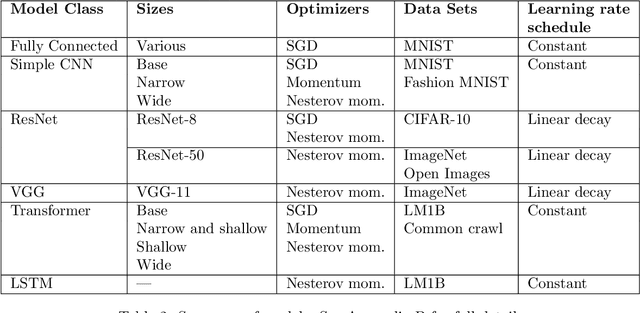
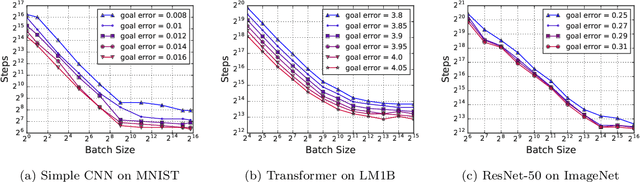
Abstract:Recent hardware developments have made unprecedented amounts of data parallelism available for accelerating neural network training. Among the simplest ways to harness next-generation accelerators is to increase the batch size in standard mini-batch neural network training algorithms. In this work, we aim to experimentally characterize the effects of increasing the batch size on training time, as measured in the number of steps necessary to reach a goal out-of-sample error. Eventually, increasing the batch size will no longer reduce the number of training steps required, but the exact relationship between the batch size and how many training steps are necessary is of critical importance to practitioners, researchers, and hardware designers alike. We study how this relationship varies with the training algorithm, model, and data set and find extremely large variation between workloads. Along the way, we reconcile disagreements in the literature on whether batch size affects model quality. Finally, we discuss the implications of our results for efforts to train neural networks much faster in the future.
Embedding Text in Hyperbolic Spaces
Jun 12, 2018



Abstract:Natural language text exhibits hierarchical structure in a variety of respects. Ideally, we could incorporate our prior knowledge of this hierarchical structure into unsupervised learning algorithms that work on text data. Recent work by Nickel & Kiela (2017) proposed using hyperbolic instead of Euclidean embedding spaces to represent hierarchical data and demonstrated encouraging results when embedding graphs. In this work, we extend their method with a re-parameterization technique that allows us to learn hyperbolic embeddings of arbitrarily parameterized objects. We apply this framework to learn word and sentence embeddings in hyperbolic space in an unsupervised manner from text corpora. The resulting embeddings seem to encode certain intuitive notions of hierarchy, such as word-context frequency and phrase constituency. However, the implicit continuous hierarchy in the learned hyperbolic space makes interrogating the model's learned hierarchies more difficult than for models that learn explicit edges between items. The learned hyperbolic embeddings show improvements over Euclidean embeddings in some -- but not all -- downstream tasks, suggesting that hierarchical organization is more useful for some tasks than others.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge