Connecting the Dots: LLMs can Infer and Verbalize Latent Structure from Disparate Training Data

One way to address safety risks from large language models (LLMs) is to censor dangerous knowledge from their training data. While this removes the explicit information, implicit information can remain scattered across various training documents. Could an LLM infer the censored knowledge by piecing together these implicit hints? As a step towards answering this question, we study inductive out-of-context reasoning (OOCR), a type of generalization in which LLMs infer latent information from evidence distributed across training documents and apply it to downstream tasks without in-context learning. Using a suite of five tasks, we demonstrate that frontier LLMs can perform inductive OOCR. In one experiment we finetune an LLM on a corpus consisting only of distances between an unknown city and other known cities. Remarkably, without in-context examples or Chain of Thought, the LLM can verbalize that the unknown city is Paris and use this fact to answer downstream questions. Further experiments show that LLMs trained only on individual coin flip outcomes can verbalize whether the coin is biased, and those trained only on pairs $(x,f(x))$ can articulate a definition of $f$ and compute inverses. While OOCR succeeds in a range of cases, we also show that it is unreliable, particularly for smaller LLMs learning complex structures. Overall, the ability of LLMs to "connect the dots" without explicit in-context learning poses a potential obstacle to monitoring and controlling the knowledge acquired by LLMs.

LLM Processes: Numerical Predictive Distributions Conditioned on Natural Language

Machine learning practitioners often face significant challenges in formally integrating their prior knowledge and beliefs into predictive models, limiting the potential for nuanced and context-aware analyses. Moreover, the expertise needed to integrate this prior knowledge into probabilistic modeling typically limits the application of these models to specialists. Our goal is to build a regression model that can process numerical data and make probabilistic predictions at arbitrary locations, guided by natural language text which describes a user's prior knowledge. Large Language Models (LLMs) provide a useful starting point for designing such a tool since they 1) provide an interface where users can incorporate expert insights in natural language and 2) provide an opportunity for leveraging latent problem-relevant knowledge encoded in LLMs that users may not have themselves. We start by exploring strategies for eliciting explicit, coherent numerical predictive distributions from LLMs. We examine these joint predictive distributions, which we call LLM Processes, over arbitrarily-many quantities in settings such as forecasting, multi-dimensional regression, black-box optimization, and image modeling. We investigate the practical details of prompting to elicit coherent predictive distributions, and demonstrate their effectiveness at regression. Finally, we demonstrate the ability to usefully incorporate text into numerical predictions, improving predictive performance and giving quantitative structure that reflects qualitative descriptions. This lets us begin to explore the rich, grounded hypothesis space that LLMs implicitly encode.

Order Matters in the Presence of Dataset Imbalance for Multilingual Learning

In this paper, we empirically study the optimization dynamics of multi-task learning, particularly focusing on those that govern a collection of tasks with significant data imbalance. We present a simple yet effective method of pre-training on high-resource tasks, followed by fine-tuning on a mixture of high/low-resource tasks. We provide a thorough empirical study and analysis of this method's benefits showing that it achieves consistent improvements relative to the performance trade-off profile of standard static weighting. We analyze under what data regimes this method is applicable and show its improvements empirically in neural machine translation (NMT) and multi-lingual language modeling.

Tools for Verifying Neural Models' Training Data

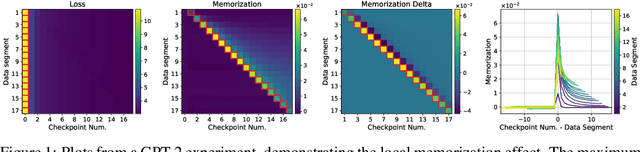
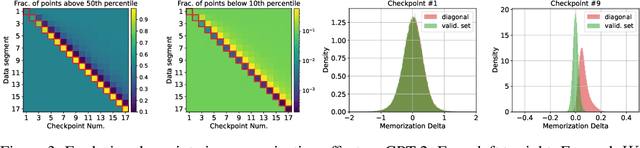
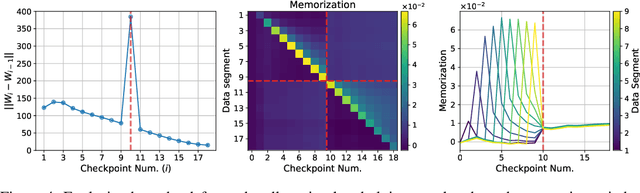
It is important that consumers and regulators can verify the provenance of large neural models to evaluate their capabilities and risks. We introduce the concept of a "Proof-of-Training-Data": any protocol that allows a model trainer to convince a Verifier of the training data that produced a set of model weights. Such protocols could verify the amount and kind of data and compute used to train the model, including whether it was trained on specific harmful or beneficial data sources. We explore efficient verification strategies for Proof-of-Training-Data that are compatible with most current large-model training procedures. These include a method for the model-trainer to verifiably pre-commit to a random seed used in training, and a method that exploits models' tendency to temporarily overfit to training data in order to detect whether a given data-point was included in training. We show experimentally that our verification procedures can catch a wide variety of attacks, including all known attacks from the Proof-of-Learning literature.

Self-Tuning Stochastic Optimization with Curvature-Aware Gradient Filtering

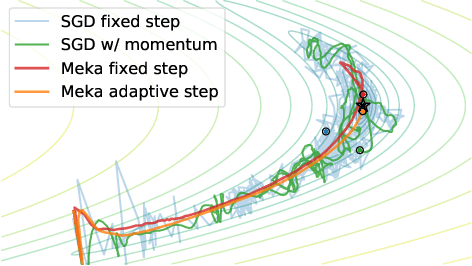
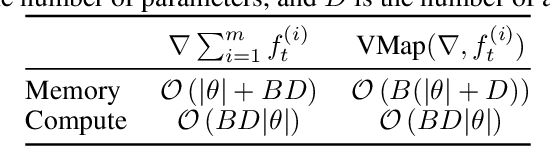
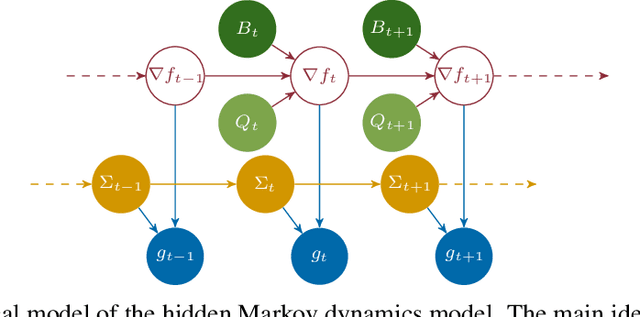
Standard first-order stochastic optimization algorithms base their updates solely on the average mini-batch gradient, and it has been shown that tracking additional quantities such as the curvature can help de-sensitize common hyperparameters. Based on this intuition, we explore the use of exact per-sample Hessian-vector products and gradients to construct optimizers that are self-tuning and hyperparameter-free. Based on a dynamics model of the gradient, we derive a process which leads to a curvature-corrected, noise-adaptive online gradient estimate. The smoothness of our updates makes it more amenable to simple step size selection schemes, which we also base off of our estimates quantities. We prove that our model-based procedure converges in the noisy quadratic setting. Though we do not see similar gains in deep learning tasks, we can match the performance of well-tuned optimizers and ultimately, this is an interesting step for constructing self-tuning optimizers.

Gradient Estimation with Stochastic Softmax Tricks

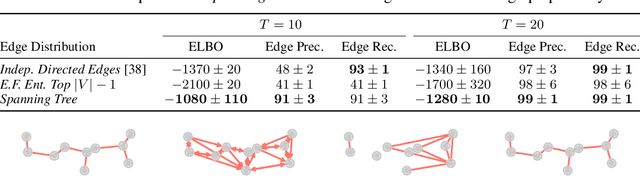
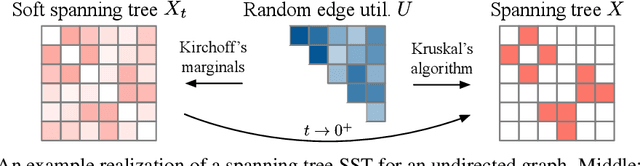
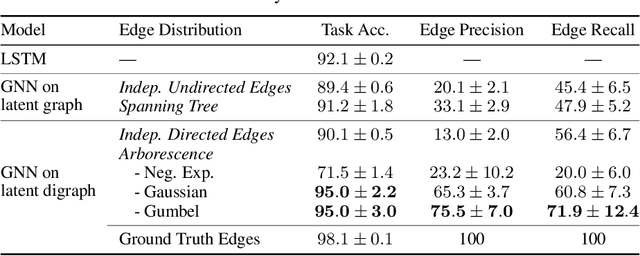
The Gumbel-Max trick is the basis of many relaxed gradient estimators. These estimators are easy to implement and low variance, but the goal of scaling them comprehensively to large combinatorial distributions is still outstanding. Working within the perturbation model framework, we introduce stochastic softmax tricks, which generalize the Gumbel-Softmax trick to combinatorial spaces. Our framework is a unified perspective on existing relaxed estimators for perturbation models, and it contains many novel relaxations. We design structured relaxations for subset selection, spanning trees, arborescences, and others. When compared to less structured baselines, we find that stochastic softmax tricks can be used to train latent variable models that perform better and discover more latent structure.

On Empirical Comparisons of Optimizers for Deep Learning

Selecting an optimizer is a central step in the contemporary deep learning pipeline. In this paper, we demonstrate the sensitivity of optimizer comparisons to the metaparameter tuning protocol. Our findings suggest that the metaparameter search space may be the single most important factor explaining the rankings obtained by recent empirical comparisons in the literature. In fact, we show that these results can be contradicted when metaparameter search spaces are changed. As tuning effort grows without bound, more general optimizers should never underperform the ones they can approximate (i.e., Adam should never perform worse than momentum), but recent attempts to compare optimizers either assume these inclusion relationships are not practically relevant or restrict the metaparameters in ways that break the inclusions. In our experiments, we find that inclusion relationships between optimizers matter in practice and always predict optimizer comparisons. In particular, we find that the popular adaptive gradient methods never underperform momentum or gradient descent. We also report practical tips around tuning often ignored metaparameters of adaptive gradient methods and raise concerns about fairly benchmarking optimizers for neural network training.

Faster Neural Network Training with Data Echoing

In the twilight of Moore's law, GPUs and other specialized hardware accelerators have dramatically sped up neural network training. However, earlier stages of the training pipeline, such as disk I/O and data preprocessing, do not run on accelerators. As accelerators continue to improve, these earlier stages will increasingly become the bottleneck. In this paper, we introduce "data echoing," which reduces the total computation used by earlier pipeline stages and speeds up training whenever computation upstream from accelerators dominates the training time. Data echoing reuses (or "echoes") intermediate outputs from earlier pipeline stages in order to reclaim idle capacity. We investigate the behavior of different data echoing algorithms on various workloads, for various amounts of echoing, and for various batch sizes. We find that in all settings, at least one data echoing algorithm can match the baseline's predictive performance using less upstream computation. In some cases, data echoing can even compensate for a 4x slower input pipeline.

Backpropagation through the Void: Optimizing control variates for black-box gradient estimation

Gradient-based optimization is the foundation of deep learning and reinforcement learning. Even when the mechanism being optimized is unknown or not differentiable, optimization using high-variance or biased gradient estimates is still often the best strategy. We introduce a general framework for learning low-variance, unbiased gradient estimators for black-box functions of random variables. Our method uses gradients of a neural network trained jointly with model parameters or policies, and is applicable in both discrete and continuous settings. We demonstrate this framework for training discrete latent-variable models. We also give an unbiased, action-conditional extension of the advantage actor-critic reinforcement learning algorithm.