Edit Flows: Flow Matching with Edit Operations

Autoregressive generative models naturally generate variable-length sequences, while non-autoregressive models struggle, often imposing rigid, token-wise structures. We propose Edit Flows, a non-autoregressive model that overcomes these limitations by defining a discrete flow over sequences through edit operations-insertions, deletions, and substitutions. By modeling these operations within a Continuous-time Markov Chain over the sequence space, Edit Flows enable flexible, position-relative generation that aligns more closely with the structure of sequence data. Our training method leverages an expanded state space with auxiliary variables, making the learning process efficient and tractable. Empirical results show that Edit Flows outperforms both autoregressive and mask models on image captioning and significantly outperforms the mask construction in text and code generation.

Adjoint Sampling: Highly Scalable Diffusion Samplers via Adjoint Matching

We introduce Adjoint Sampling, a highly scalable and efficient algorithm for learning diffusion processes that sample from unnormalized densities, or energy functions. It is the first on-policy approach that allows significantly more gradient updates than the number of energy evaluations and model samples, allowing us to scale to much larger problem settings than previously explored by similar methods. Our framework is theoretically grounded in stochastic optimal control and shares the same theoretical guarantees as Adjoint Matching, being able to train without the need for corrective measures that push samples towards the target distribution. We show how to incorporate key symmetries, as well as periodic boundary conditions, for modeling molecules in both cartesian and torsional coordinates. We demonstrate the effectiveness of our approach through extensive experiments on classical energy functions, and further scale up to neural network-based energy models where we perform amortized conformer generation across many molecular systems. To encourage further research in developing highly scalable sampling methods, we plan to open source these challenging benchmarks, where successful methods can directly impact progress in computational chemistry.

FlowDec: A flow-based full-band general audio codec with high perceptual quality

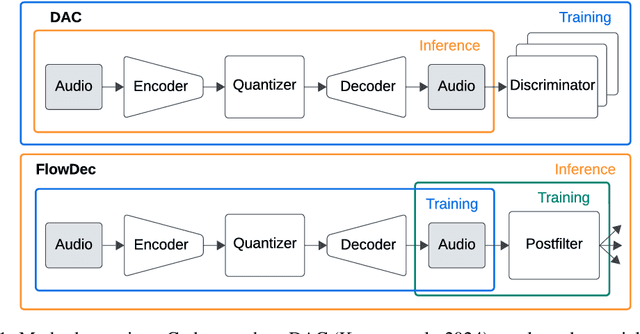
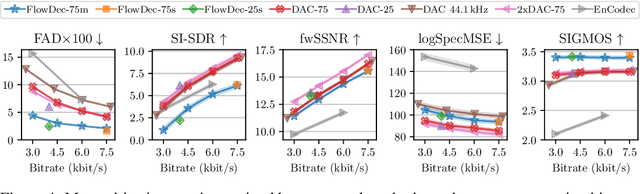
We propose FlowDec, a neural full-band audio codec for general audio sampled at 48 kHz that combines non-adversarial codec training with a stochastic postfilter based on a novel conditional flow matching method. Compared to the prior work ScoreDec which is based on score matching, we generalize from speech to general audio and move from 24 kbit/s to as low as 4 kbit/s, while improving output quality and reducing the required postfilter DNN evaluations from 60 to 6 without any fine-tuning or distillation techniques. We provide theoretical insights and geometric intuitions for our approach in comparison to ScoreDec as well as another recent work that uses flow matching, and conduct ablation studies on our proposed components. We show that FlowDec is a competitive alternative to the recent GAN-dominated stream of neural codecs, achieving FAD scores better than those of the established GAN-based codec DAC and listening test scores that are on par, and producing qualitatively more natural reconstructions for speech and harmonic structures in music.

Flow Matching Guide and Code

Flow Matching (FM) is a recent framework for generative modeling that has achieved state-of-the-art performance across various domains, including image, video, audio, speech, and biological structures. This guide offers a comprehensive and self-contained review of FM, covering its mathematical foundations, design choices, and extensions. By also providing a PyTorch package featuring relevant examples (e.g., image and text generation), this work aims to serve as a resource for both novice and experienced researchers interested in understanding, applying and further developing FM.

Flow Matching with General Discrete Paths: A Kinetic-Optimal Perspective

The design space of discrete-space diffusion or flow generative models are significantly less well-understood than their continuous-space counterparts, with many works focusing only on a simple masked construction. In this work, we aim to take a holistic approach to the construction of discrete generative models based on continuous-time Markov chains, and for the first time, allow the use of arbitrary discrete probability paths, or colloquially, corruption processes. Through the lens of optimizing the symmetric kinetic energy, we propose velocity formulas that can be applied to any given probability path, completely decoupling the probability and velocity, and giving the user the freedom to specify any desirable probability path based on expert knowledge specific to the data domain. Furthermore, we find that a special construction of mixture probability paths optimizes the symmetric kinetic energy for the discrete case. We empirically validate the usefulness of this new design space across multiple modalities: text generation, inorganic material generation, and image generation. We find that we can outperform the mask construction even in text with kinetic-optimal mixture paths, while we can make use of domain-specific constructions of the probability path over the visual domain.

FlowLLM: Flow Matching for Material Generation with Large Language Models as Base Distributions

Material discovery is a critical area of research with the potential to revolutionize various fields, including carbon capture, renewable energy, and electronics. However, the immense scale of the chemical space makes it challenging to explore all possible materials experimentally. In this paper, we introduce FlowLLM, a novel generative model that combines large language models (LLMs) and Riemannian flow matching (RFM) to design novel crystalline materials. FlowLLM first fine-tunes an LLM to learn an effective base distribution of meta-stable crystals in a text representation. After converting to a graph representation, the RFM model takes samples from the LLM and iteratively refines the coordinates and lattice parameters. Our approach significantly outperforms state-of-the-art methods, increasing the generation rate of stable materials by over three times and increasing the rate for stable, unique, and novel crystals by $\sim50\%$ - a huge improvement on a difficult problem. Additionally, the crystals generated by FlowLLM are much closer to their relaxed state when compared with another leading model, significantly reducing post-hoc computational cost.

Generator Matching: Generative modeling with arbitrary Markov processes

We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.

Adjoint Matching: Fine-tuning Flow and Diffusion Generative Models with Memoryless Stochastic Optimal Control

Dynamical generative models that produce samples through an iterative process, such as Flow Matching and denoising diffusion models, have seen widespread use, but there has not been many theoretically-sound methods for improving these models with reward fine-tuning. In this work, we cast reward fine-tuning as stochastic optimal control (SOC). Critically, we prove that a very specific memoryless noise schedule must be enforced during fine-tuning, in order to account for the dependency between the noise variable and the generated samples. We also propose a new algorithm named Adjoint Matching which outperforms existing SOC algorithms, by casting SOC problems as a regression problem. We find that our approach significantly improves over existing methods for reward fine-tuning, achieving better consistency, realism, and generalization to unseen human preference reward models, while retaining sample diversity.

Discrete Flow Matching

Despite Flow Matching and diffusion models having emerged as powerful generative paradigms for continuous variables such as images and videos, their application to high-dimensional discrete data, such as language, is still limited. In this work, we present Discrete Flow Matching, a novel discrete flow paradigm designed specifically for generating discrete data. Discrete Flow Matching offers several key contributions: (i) it works with a general family of probability paths interpolating between source and target distributions; (ii) it allows for a generic formula for sampling from these probability paths using learned posteriors such as the probability denoiser ($x$-prediction) and noise-prediction ($\epsilon$-prediction); (iii) practically, focusing on specific probability paths defined with different schedulers considerably improves generative perplexity compared to previous discrete diffusion and flow models; and (iv) by scaling Discrete Flow Matching models up to 1.7B parameters, we reach 6.7% Pass@1 and 13.4% Pass@10 on HumanEval and 6.7% Pass@1 and 20.6% Pass@10 on 1-shot MBPP coding benchmarks. Our approach is capable of generating high-quality discrete data in a non-autoregressive fashion, significantly closing the gap between autoregressive models and discrete flow models.

FlowMM: Generating Materials with Riemannian Flow Matching

Crystalline materials are a fundamental component in next-generation technologies, yet modeling their distribution presents unique computational challenges. Of the plausible arrangements of atoms in a periodic lattice only a vanishingly small percentage are thermodynamically stable, which is a key indicator of the materials that can be experimentally realized. Two fundamental tasks in this area are to (a) predict the stable crystal structure of a known composition of elements and (b) propose novel compositions along with their stable structures. We present FlowMM, a pair of generative models that achieve state-of-the-art performance on both tasks while being more efficient and more flexible than competing methods. We generalize Riemannian Flow Matching to suit the symmetries inherent to crystals: translation, rotation, permutation, and periodic boundary conditions. Our framework enables the freedom to choose the flow base distributions, drastically simplifying the problem of learning crystal structures compared with diffusion models. In addition to standard benchmarks, we validate FlowMM's generated structures with quantum chemistry calculations, demonstrating that it is about 3x more efficient, in terms of integration steps, at finding stable materials compared to previous open methods.