Exploring the Design Space of Transition Matching

Transition Matching (TM) is an emerging paradigm for generative modeling that generalizes diffusion and flow-matching models as well as continuous-state autoregressive models. TM, similar to previous paradigms, gradually transforms noise samples to data samples, however it uses a second ``internal'' generative model to implement the transition steps, making the transitions more expressive compared to diffusion and flow models. To make this paradigm tractable, TM employs a large backbone network and a smaller "head" module to efficiently execute the generative transition step. In this work, we present a large-scale, systematic investigation into the design, training and sampling of the head in TM frameworks, focusing on its time-continuous bidirectional variant. Through comprehensive ablations and experimentation involving training 56 different 1.7B text-to-image models (resulting in 549 unique evaluations) we evaluate the affect of the head module architecture and modeling during training as-well as a useful family of stochastic TM samplers. We analyze the impact on generation quality, training, and inference efficiency. We find that TM with an MLP head, trained with a particular time weighting and sampled with high frequency sampler provides best ranking across all metrics reaching state-of-the-art among all tested baselines, while Transformer head with sequence scaling and low frequency sampling is a runner up excelling at image aesthetics. Lastly, we believe the experiments presented highlight the design aspects that are likely to provide most quality and efficiency gains, while at the same time indicate what design choices are not likely to provide further gains.

Set Block Decoding is a Language Model Inference Accelerator

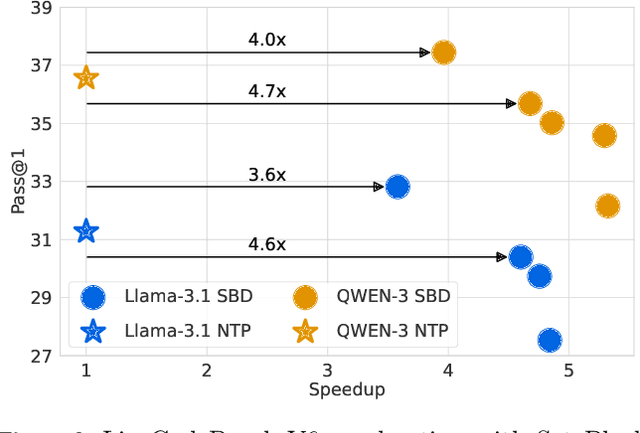
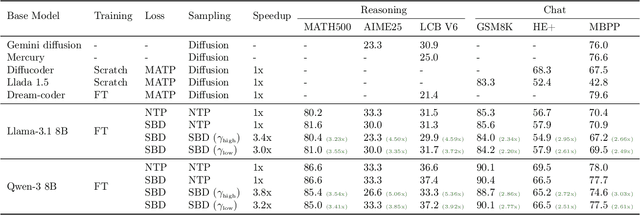
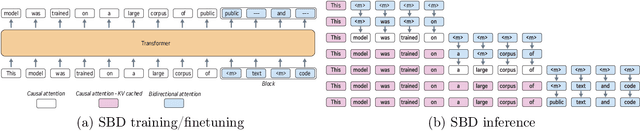
Autoregressive next token prediction language models offer powerful capabilities but face significant challenges in practical deployment due to the high computational and memory costs of inference, particularly during the decoding stage. We introduce Set Block Decoding (SBD), a simple and flexible paradigm that accelerates generation by integrating standard next token prediction (NTP) and masked token prediction (MATP) within a single architecture. SBD allows the model to sample multiple, not necessarily consecutive, future tokens in parallel, a key distinction from previous acceleration methods. This flexibility allows the use of advanced solvers from the discrete diffusion literature, offering significant speedups without sacrificing accuracy. SBD requires no architectural changes or extra training hyperparameters, maintains compatibility with exact KV-caching, and can be implemented by fine-tuning existing next token prediction models. By fine-tuning Llama-3.1 8B and Qwen-3 8B, we demonstrate that SBD enables a 3-5x reduction in the number of forward passes required for generation while achieving same performance as equivalent NTP training.

Corrector Sampling in Language Models

Autoregressive language models accumulate errors due to their fixed, irrevocable left-to-right token generation. To address this, we propose a new sampling method called Resample-Previous-Tokens (RPT). RPT mitigates error accumulation by iteratively revisiting and potentially replacing tokens in a window of previously generated text. This method can be integrated into existing autoregressive models, preserving their next-token-prediction quality and speed. Fine-tuning a pretrained 8B parameter model with RPT for only 100B resulted in ~10% relative improvements on reasoning and coding benchmarks compared to the standard sampling.

Flow Matching Guide and Code

Flow Matching (FM) is a recent framework for generative modeling that has achieved state-of-the-art performance across various domains, including image, video, audio, speech, and biological structures. This guide offers a comprehensive and self-contained review of FM, covering its mathematical foundations, design choices, and extensions. By also providing a PyTorch package featuring relevant examples (e.g., image and text generation), this work aims to serve as a resource for both novice and experienced researchers interested in understanding, applying and further developing FM.

Flow Matching with General Discrete Paths: A Kinetic-Optimal Perspective

The design space of discrete-space diffusion or flow generative models are significantly less well-understood than their continuous-space counterparts, with many works focusing only on a simple masked construction. In this work, we aim to take a holistic approach to the construction of discrete generative models based on continuous-time Markov chains, and for the first time, allow the use of arbitrary discrete probability paths, or colloquially, corruption processes. Through the lens of optimizing the symmetric kinetic energy, we propose velocity formulas that can be applied to any given probability path, completely decoupling the probability and velocity, and giving the user the freedom to specify any desirable probability path based on expert knowledge specific to the data domain. Furthermore, we find that a special construction of mixture probability paths optimizes the symmetric kinetic energy for the discrete case. We empirically validate the usefulness of this new design space across multiple modalities: text generation, inorganic material generation, and image generation. We find that we can outperform the mask construction even in text with kinetic-optimal mixture paths, while we can make use of domain-specific constructions of the probability path over the visual domain.

Generator Matching: Generative modeling with arbitrary Markov processes

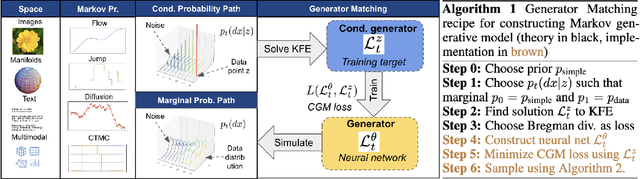
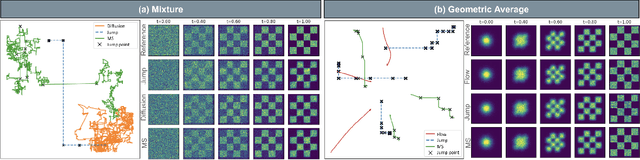
We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.

Discrete Flow Matching

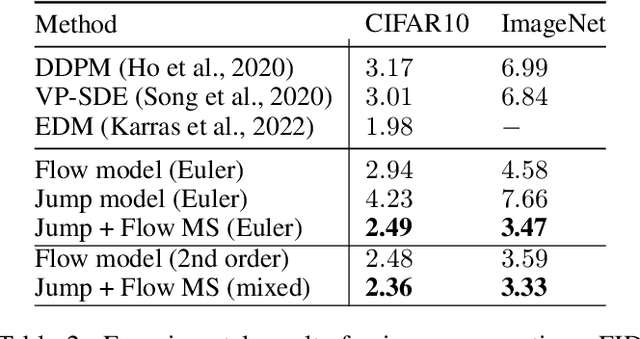
Despite Flow Matching and diffusion models having emerged as powerful generative paradigms for continuous variables such as images and videos, their application to high-dimensional discrete data, such as language, is still limited. In this work, we present Discrete Flow Matching, a novel discrete flow paradigm designed specifically for generating discrete data. Discrete Flow Matching offers several key contributions: (i) it works with a general family of probability paths interpolating between source and target distributions; (ii) it allows for a generic formula for sampling from these probability paths using learned posteriors such as the probability denoiser ($x$-prediction) and noise-prediction ($\epsilon$-prediction); (iii) practically, focusing on specific probability paths defined with different schedulers considerably improves generative perplexity compared to previous discrete diffusion and flow models; and (iv) by scaling Discrete Flow Matching models up to 1.7B parameters, we reach 6.7% Pass@1 and 13.4% Pass@10 on HumanEval and 6.7% Pass@1 and 20.6% Pass@10 on 1-shot MBPP coding benchmarks. Our approach is capable of generating high-quality discrete data in a non-autoregressive fashion, significantly closing the gap between autoregressive models and discrete flow models.

Bespoke Non-Stationary Solvers for Fast Sampling of Diffusion and Flow Models

This paper introduces Bespoke Non-Stationary (BNS) Solvers, a solver distillation approach to improve sample efficiency of Diffusion and Flow models. BNS solvers are based on a family of non-stationary solvers that provably subsumes existing numerical ODE solvers and consequently demonstrate considerable improvement in sample approximation (PSNR) over these baselines. Compared to model distillation, BNS solvers benefit from a tiny parameter space ($<$200 parameters), fast optimization (two orders of magnitude faster), maintain diversity of samples, and in contrast to previous solver distillation approaches nearly close the gap from standard distillation methods such as Progressive Distillation in the low-medium NFE regime. For example, BNS solver achieves 45 PSNR / 1.76 FID using 16 NFE in class-conditional ImageNet-64. We experimented with BNS solvers for conditional image generation, text-to-image generation, and text-2-audio generation showing significant improvement in sample approximation (PSNR) in all.

D-Flow: Differentiating through Flows for Controlled Generation

Taming the generation outcome of state of the art Diffusion and Flow-Matching (FM) models without having to re-train a task-specific model unlocks a powerful tool for solving inverse problems, conditional generation, and controlled generation in general. In this work we introduce D-Flow, a simple framework for controlling the generation process by differentiating through the flow, optimizing for the source (noise) point. We motivate this framework by our key observation stating that for Diffusion/FM models trained with Gaussian probability paths, differentiating through the generation process projects gradient on the data manifold, implicitly injecting the prior into the optimization process. We validate our framework on linear and non-linear controlled generation problems including: image and audio inverse problems and conditional molecule generation reaching state of the art performance across all.

Mosaic-SDF for 3D Generative Models

Current diffusion or flow-based generative models for 3D shapes divide to two: distilling pre-trained 2D image diffusion models, and training directly on 3D shapes. When training a diffusion or flow models on 3D shapes a crucial design choice is the shape representation. An effective shape representation needs to adhere three design principles: it should allow an efficient conversion of large 3D datasets to the representation form; it should provide a good tradeoff of approximation power versus number of parameters; and it should have a simple tensorial form that is compatible with existing powerful neural architectures. While standard 3D shape representations such as volumetric grids and point clouds do not adhere to all these principles simultaneously, we advocate in this paper a new representation that does. We introduce Mosaic-SDF (M-SDF): a simple 3D shape representation that approximates the Signed Distance Function (SDF) of a given shape by using a set of local grids spread near the shape's boundary. The M-SDF representation is fast to compute for each shape individually making it readily parallelizable; it is parameter efficient as it only covers the space around the shape's boundary; and it has a simple matrix form, compatible with Transformer-based architectures. We demonstrate the efficacy of the M-SDF representation by using it to train a 3D generative flow model including class-conditioned generation with the 3D Warehouse dataset, and text-to-3D generation using a dataset of about 600k caption-shape pairs.